
Логические выражения
Запись сложного высказывания в виде простых высказываний, соединенных логическими связками, называется логической формулой. Напр., «Если мы поедем во Францию, то увидим Эйфелеву башню» - формула: А В.
Тавталогия – это формула, истинная при любом наборе входящих в нее переменных. Например, x v x (быть или не быть).
Противоречие – это формула, ложная при любом наборе входящих в нее переменных. Например, x & x (я и не я).
Замечание: При записи выражения учитывается приоритет операций. Высший приоритет имеет операция отрицание, затем конъюнкция, затем дизъюнкция, затем функции.
Упражнения на составление формул:
Если мистер Джонс счастлив, то мисс Джонс несчастлива, и если мисс Джонс счастлива, то мистер Джонс несчастлив. (А ) & ( B)
Если влажность так высока, то либо после полудня, либо вечером будет дождь. А(ВvC)
Если ни в Варшаву мы не поедем, ни в горы мы не пойдем, то мы ежедневно будем ходить на пляж или если будет дождь, то будем читать книги.
Если «Спартак» и «Динамо» проиграет, а «Торпедо» выиграет, то «Локомотив» потеряет первое место, а на третье место выйдет «Зенит».
Правильно ли рассуждение: «Если Джонс – коммунист, то Джонс – атеист. Джонс – атеист. Следовательно, Джонс – коммунист. (А В) & (ВА)1
Записать выражение. Сформулировать отрицание. «Если летом будет дождливая погода, то ни купаться, ни загорать нам не удастся».
Автопилот может работать, если исправен главный бортовой компьютер или два вспомогательных. Выполните формализацию и запишите логические формулы для высказываний “автопилот работоспособен” и “автопилот неработоспособен”.
Любая операция алгебры высказываний может быть выражена через три основные операции: And, Or, Not.
![]()
![]()
![]()
![]()
![]() =
=![]()
Доказать эти тождества можно построением таблицы истинности.
Построить
таблицу истинности логического выражения
![]()
Таблица содержит 1+4 строки (две переменные могут иметь 4 возможных комбинаций значений) и 2+3 столбца (2 переменные и 3 операции).
При построении таблицы следует учитывать порядок приоритета выполнения операций: сначала выполняются операции Или, затем логическое следование.
x |
y |
xy |
|
|
0 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
Практическая работа. Построение логических выражений в Excel
Построить ТИ выражения в Excel.
Формулы в шапке таблицы выполнить в редакторе формул.
Использовать логические функции Excel для получения значений в ячейках таблицы.
Замечание. Операция импликация может выполняться функцией ЕСЛИ(условие; выражение1; выражение2), в этом случае условие оставляем пустым, первый аргумент указываем в качестве выражения1, а второй - выражение2.
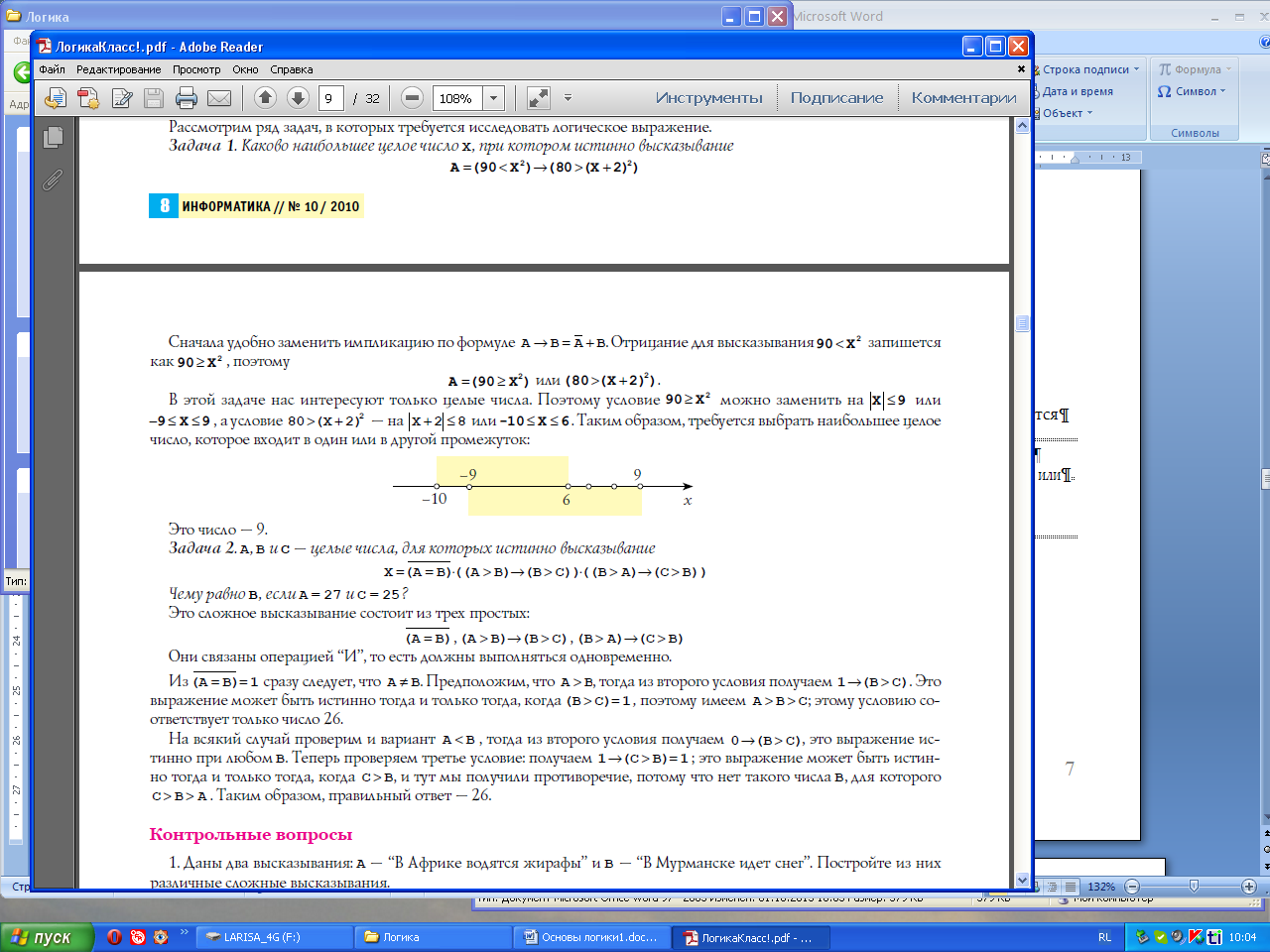
Рассмотрим ряд задач, в которых требуется исследовать логическое выражение.
Задача 1. Каково наибольшее целое число X, при котором истинно высказывание
A (90 X2)(80 (X 2)2)
Д/з:
Даны два высказывания: A — “В Африке водятся жирафы” и B — “В Мурманске идет снег”. Постройте из них различные сложные высказывания.
Почему в таблице истинности для операции “НЕ” две строки, а для других изученных операций — четыре? Сколько строчек в таблице истинности выражения с тремя переменными? с четырьмя? с пятью?
Построить таблицы истинности:
x
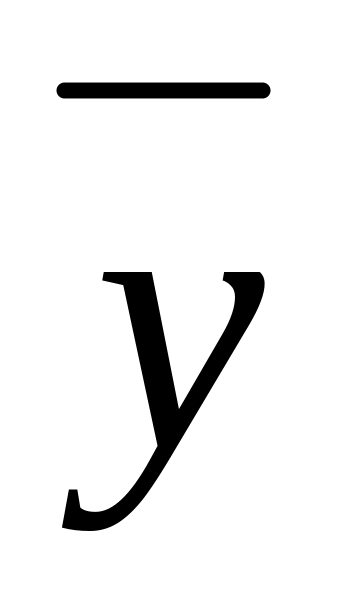
x y x
x y
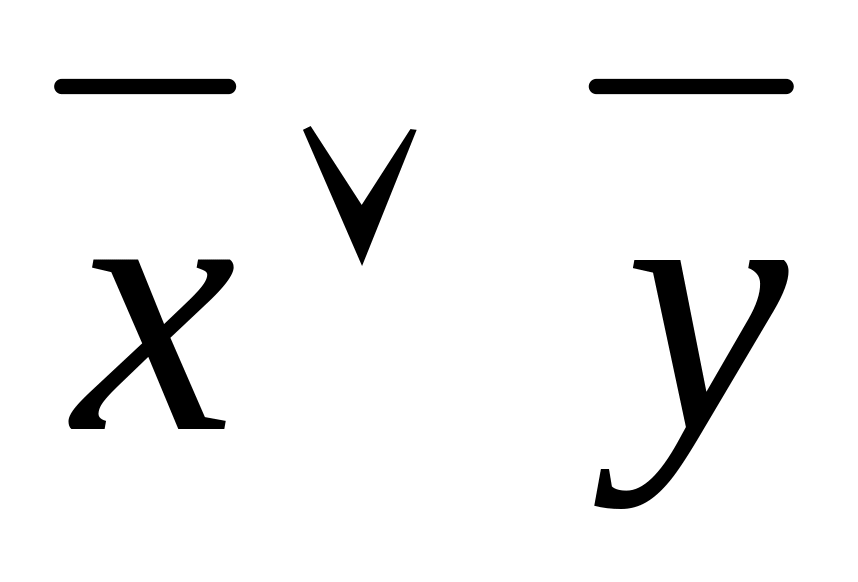
xx yz
x y z
x y z
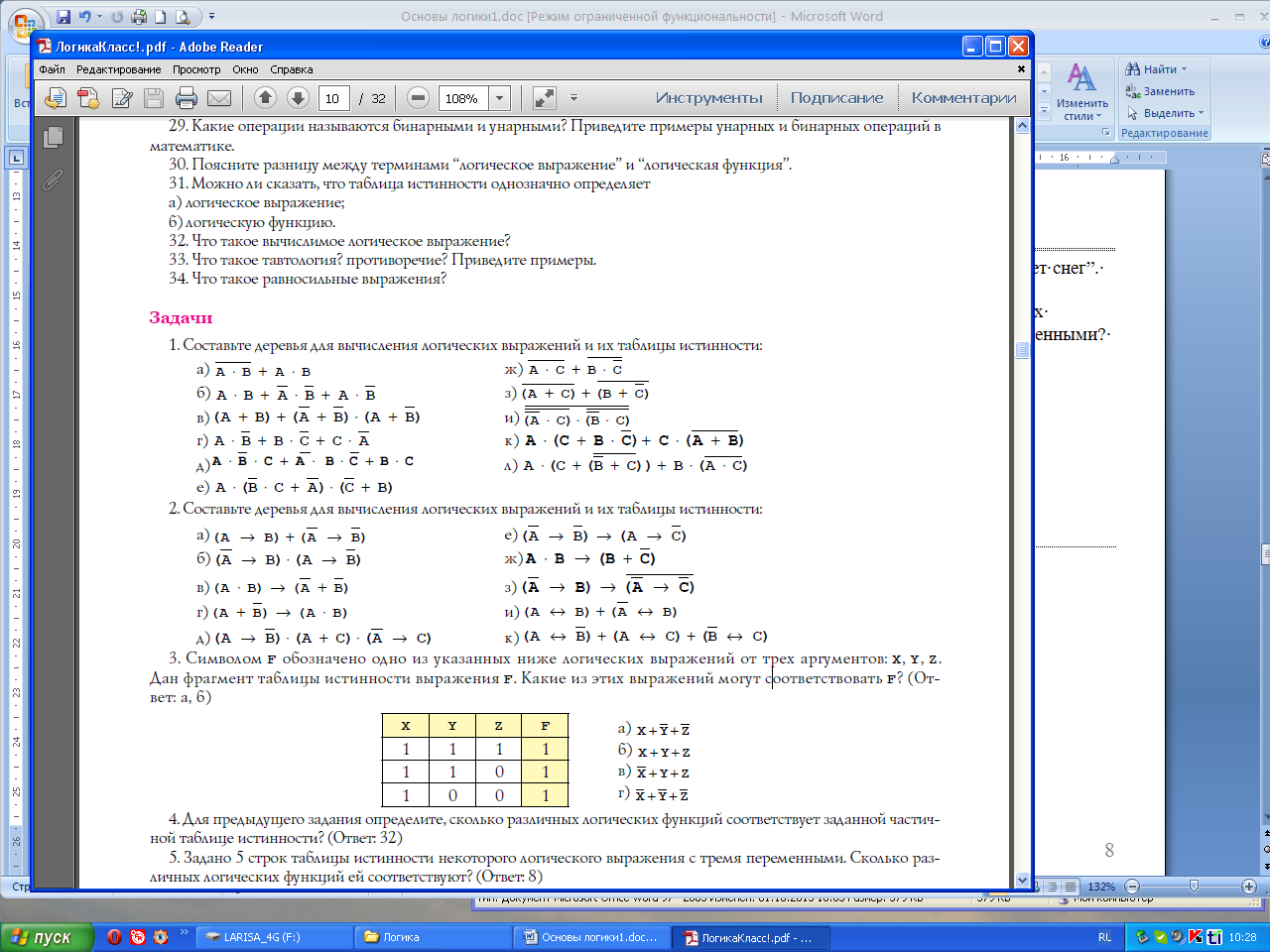
Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z. Дан фрагмент таблицы истинности выражения F. Какие из этих выражений могут соответствовать F? (Ответ: а, б)
X |
Y |
Z |
F |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
а)
X ![]()
![]()
б) X YZ
в)
![]() YZ
YZ
г)
![]()
Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z. Дан фрагмент таблицы истинности выражения F. Какие из этих выражений могут соответствовать F? (Ответ: б, г)
X |
Y |
Z |
F |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
б)
X![]() Y
Y![]()
в)
![]() Z
Z
г)
X ![]() Z
Z
Определите значение логического выражения (X > 2)→(X > 3) для X = 1, 2, 3, 4.
(Ответ: 1, 1, 0, 1)
Определите значение логического выражения
((X < 5)→(X < 3)) ((X < 2)→(X < 1)) для X = 1, 2, 3, 4.
(Ответ: 0, 1, 0, 0)
Определите значение логического выражения
((X > 3)+(X < 3))→(X < 1) для X = 1, 2, 3, 4.
(Ответ: 0, 0, 1, 0)
Определите значение логического выражения
((X < 4)→(X < 3)) ((X < 3)→(X < 1)) для X = 1, 2, 3, 4.
(Ответ: 0, 0, 0, 1)
Найдите все целые значения X, при которых логическое выражение
(X > 2)→(X > 5) ложно.
(Ответ: 3, 4, 5)
Найдите все целые значения X, при которых логическое выражение
((X > 0)+(X > 4))→(X > 4) ложно.
(Ответ: 1, 2, 3, 4)
Каково наибольшее целое положительное число X, при котором истинно высказывание:
(X2-1>100) → (X(X-1)<100)?
(Ответ: 10)
Известно, что для чисел A, B и C истинно высказывание
![]() ((B
<A)(2C
>A))((A
<B)
(A>2C)).
((B
<A)(2C
>A))((A
<B)
(A>2C)).
Чему равно A, если C = 10 и B = 22? (Ответ: 21)
Логические законы.
Закон
двойного отрицания: ![]() =A
=A
Закон не противоречия. Высказывание не может быть истинным и ложным одновременно. А & = 0 Закон исключенного третьего. Высказывание может быть истинным или ложным, третьего не дано. А =1 Закон дистрибутивности: (A & B) (A & C) = A & (B C), (A B) & (A C) = A (B & C), Законы поглощения: A (A & B) = A A &(A B) = A Законы исключения:
Как видим, законы логики симметричны относительно операций “И”, “ИЛИ”:
|
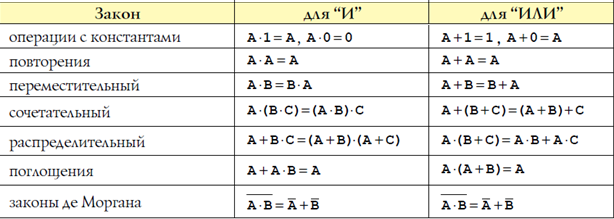
Любое из этих соотношений можно доказать построением таблицы истинности. Например, докажем закон поглощения A (A & B) = A.
А |
В |
A & B |
F |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
Доказать законы Де Моргана, закон дистрибутивности, законы исключения.
Упражнения:
Если я поздно приду на остановку и не смогу сесть в автобус, то опоздаю на занятия и пропущу интересную лекцию. Записать выражение. Сформулировать отрицание.
Если завтра будет воскресенье или в институте не будет занятий, то ко мне придут друзья, и мы послушаем музыку. Записать выражение. Сформулировать отрицание.
После обеда я отправлюсь на прогулку в парк, и если ко мне зайдет приятель, буду играть с ним в шахматы или мы посмотрим кино. Записать выражение. Сформулировать отрицание.
Преобразование логических выражений.
Применяя законы логики можно выполнять преобразования логических выражений. Например, докажем законы исключения:
![]()
(A & B) ( & B) = B &(A )= B & 1 = B
(A B) & ( B) = B (A & )= B 0 = B
Теперь с помощью приведенных законов алгебры логики упростим полученное ранее логическое выражение для объединения областей 3 и 4 на диаграмме Венна с тремя переменными (стр.3):
![]() +
+![]() .=(A
+
.=(A
+ ![]() )
)![]() .=
.=![]()
Здесь мы сначала вынесли общий множитель двух слагаемых за скобки, а затем применили закон исключения третьего.
В общем случае можно рекомендовать такую последовательность действий:
1. Заменить все “небазовые” операции (исключающее ИЛИ, импликацию, эквивалентность и др.) на их выражения через базовые операции “НЕ”, “И” и “ИЛИ”.
2. Раскрыть отрицания сложных выражений по законам де Моргана так, чтобы операции отрицания остались только у отдельных переменных.
3. Используя вынесение общих множителей за скобки, раскрытие скобок и другие законы алгебры логики, упростить выражение.
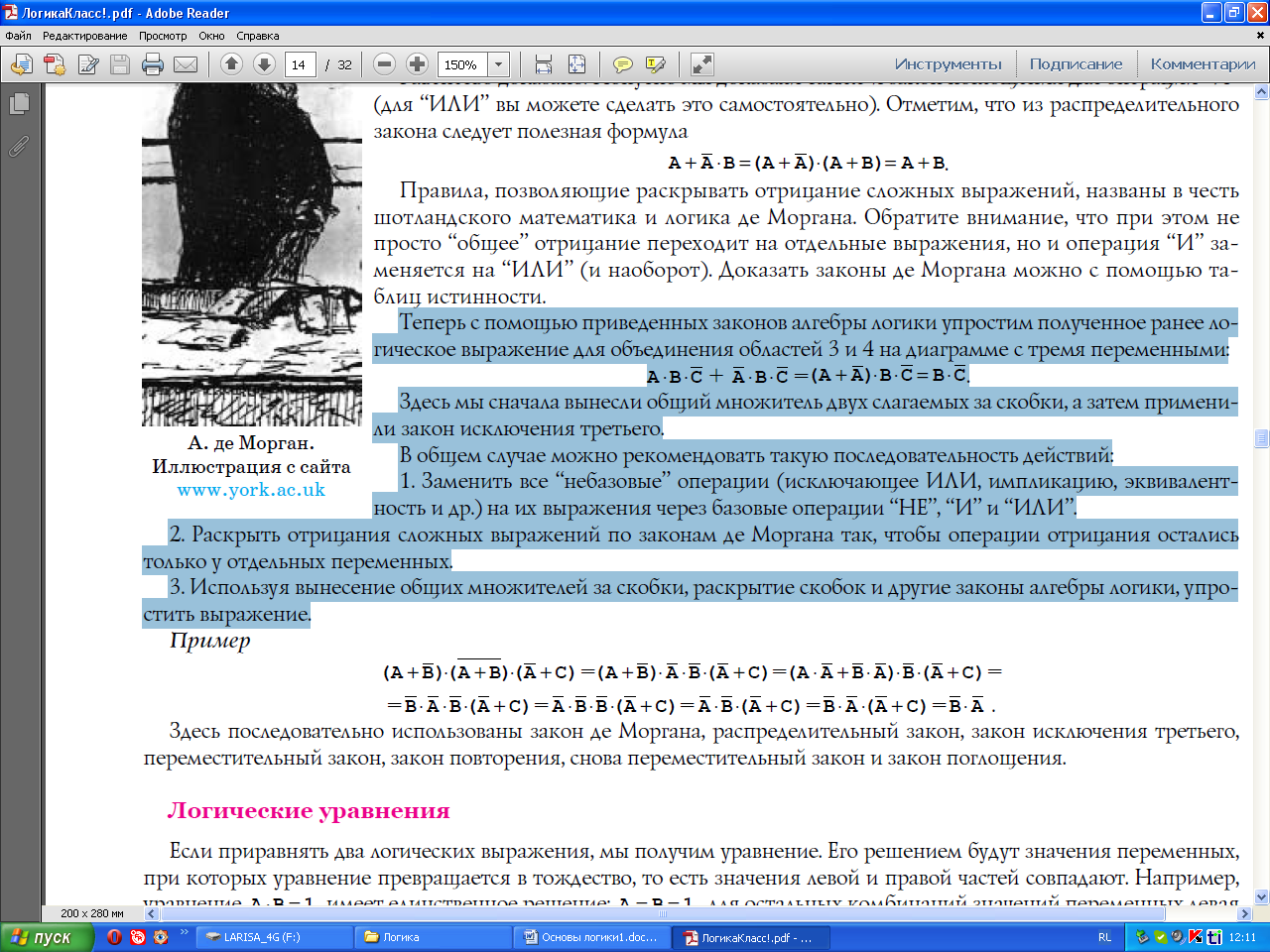
Упражнения. Упростить выражения. Проверить построением таблицы истинности.

A ( & B);
A & ( B);
(A & B & ) (A & ) (B & C &
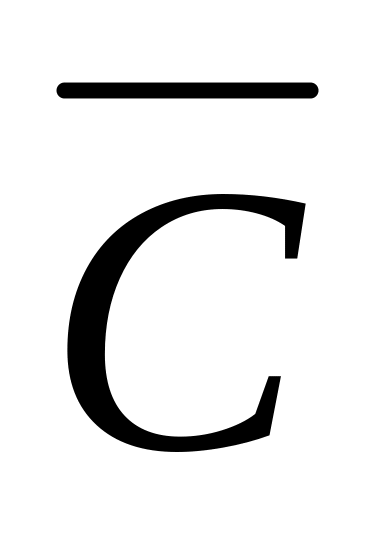 );
);(A & B & ) (A & B& C)
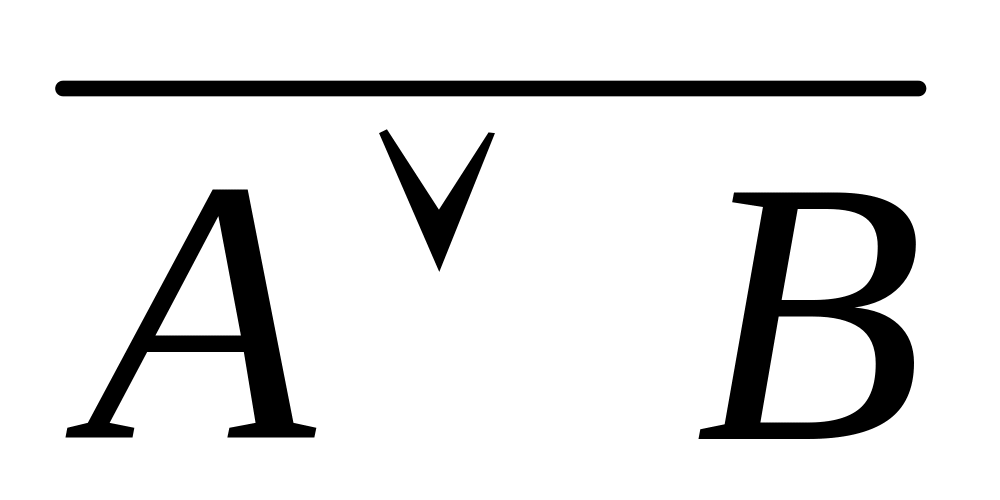 ;
;(A B) & ( A) & ( B);
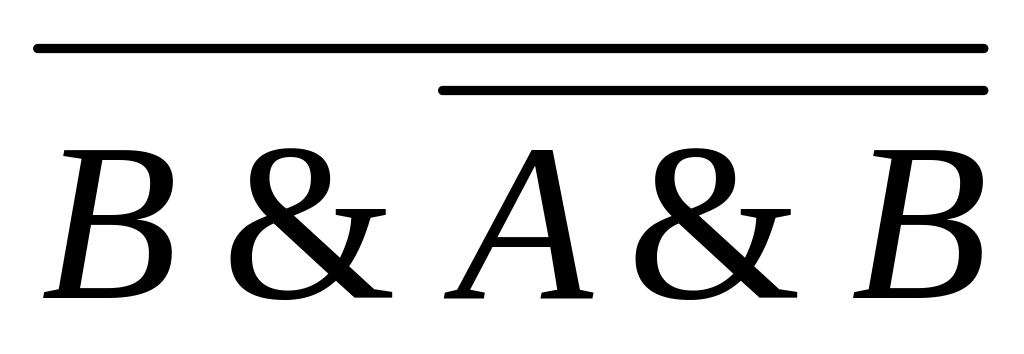 ;
;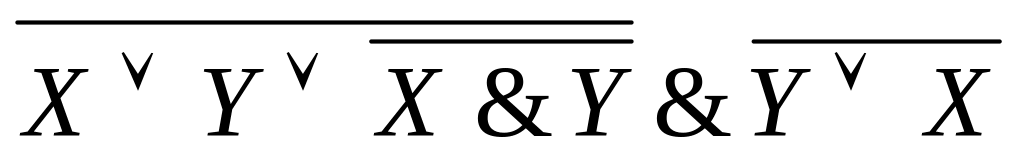 ;
;XXY;
(XY) XY;
(A & B) (A B);
((C B) B) &(A & B) B;
((C B) B) &(A B) B;
(A B) & A .
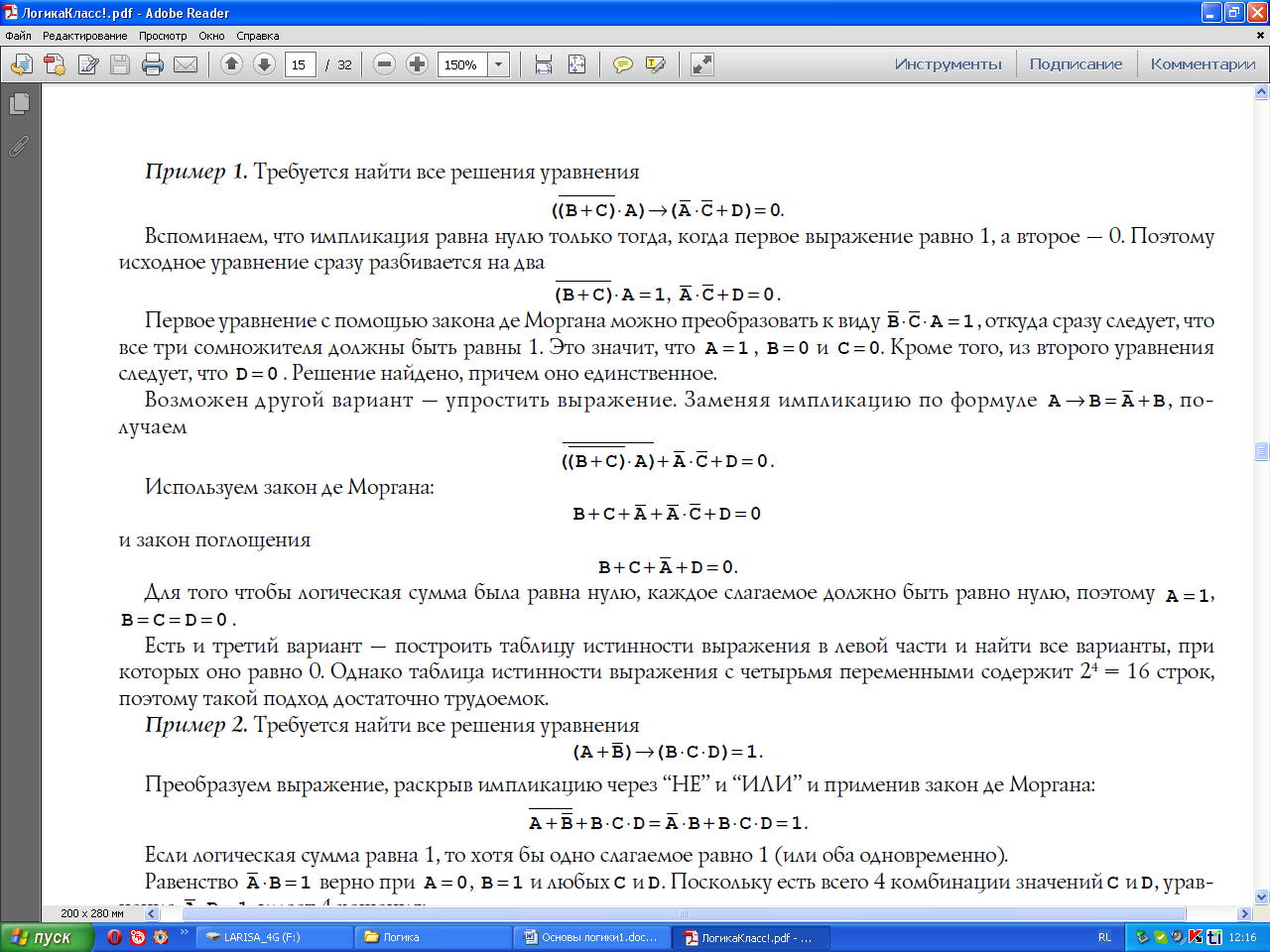
Решение логических уравнений
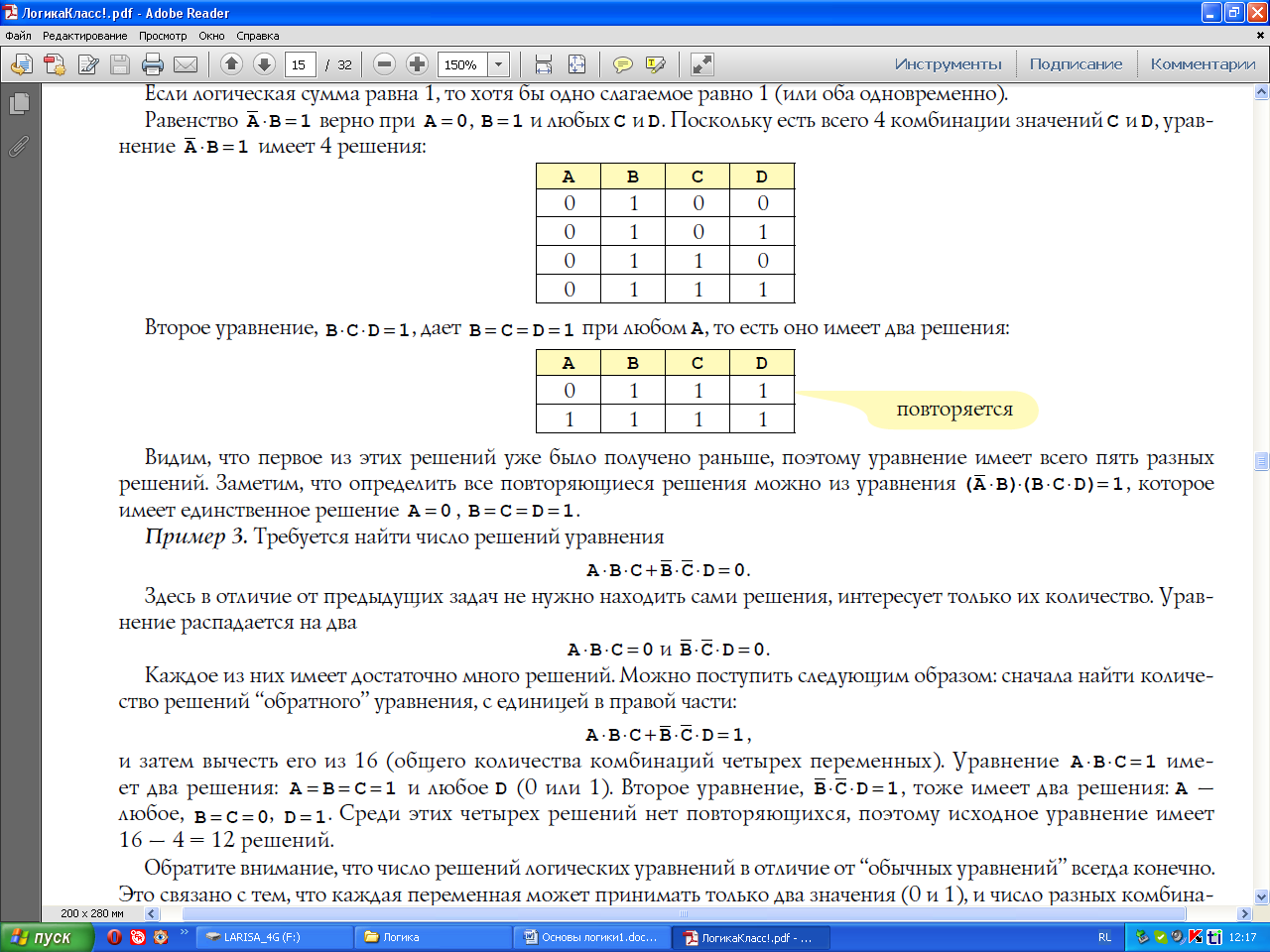
Если приравнять два логических выражения, мы получим уравнение. Его решением будут значения переменных, при которых уравнение превращается в тождество, то есть значения левой и правой частей совпадают. Например, уравнение AB = 1 имеет единственное решение: A = B = 1, для остальных комбинаций значений переменных левая часть равна нулю.
В то же время. уравнение A + B = 1 имеет три решения: ( A = 0, B = 1, A = 1, B = 0 и A = B = 1).

Решение логических задач.

Кто из учеников A, B, C, D играет, а кто не играет в шахматы, если известно следующее:
если A или В играет, то С не играет;
если В не играет, то играют С и D;
С играет.
Ответ: играют ученики С и D, а А и В не играют.
Кто из трех студентов изучает логику, если известно:
Если изучает первый, то изучает и третий, но неверно, что если изучает второй, то изучает третий.
Ответ: Второй.
На вопрос, какая завтра будет погода, синоптик ответил:
если не будет ветра, то будет пасмурно без дождя;
если будет дождь, то будет пасмурно и без ветра;
если будет пасмурная погода, то будет дождь и не будет ветра.
Ответ: будет ясная погода, но с ветром.
Определить, кто из четырех студентов сдал экзамены, если известно:
Если первый сдал, то и второй сдал;
Если второй сдал, то третий сдал или первый не сдал;
Если четвертый не сдал, то первый сдал, а третий не сдал;
Если четвертый сдал, то и первый сдал.
Ответ: все сдали.
