2. Диаграммы

Выражения, зависящие от небольшого количества переменных (обычно не более четырех), удобно изображать в виде диаграмм, которые называют диаграммами Венна, или кругами Эйлера.

На такой диаграмме каждой переменной соответствует круг, внутри которого она равна единице, а вне его — нулю. Круги пересекаются, каждый с каждым. Области, в которых рассматриваемое логическое выражение истинно, закрашиваются каким-либо цветом. Ниже приведены диаграммы для простейших операций с одной и двумя переменными. Серым цветом залиты области, где рассматриваемое выражение равно единице.

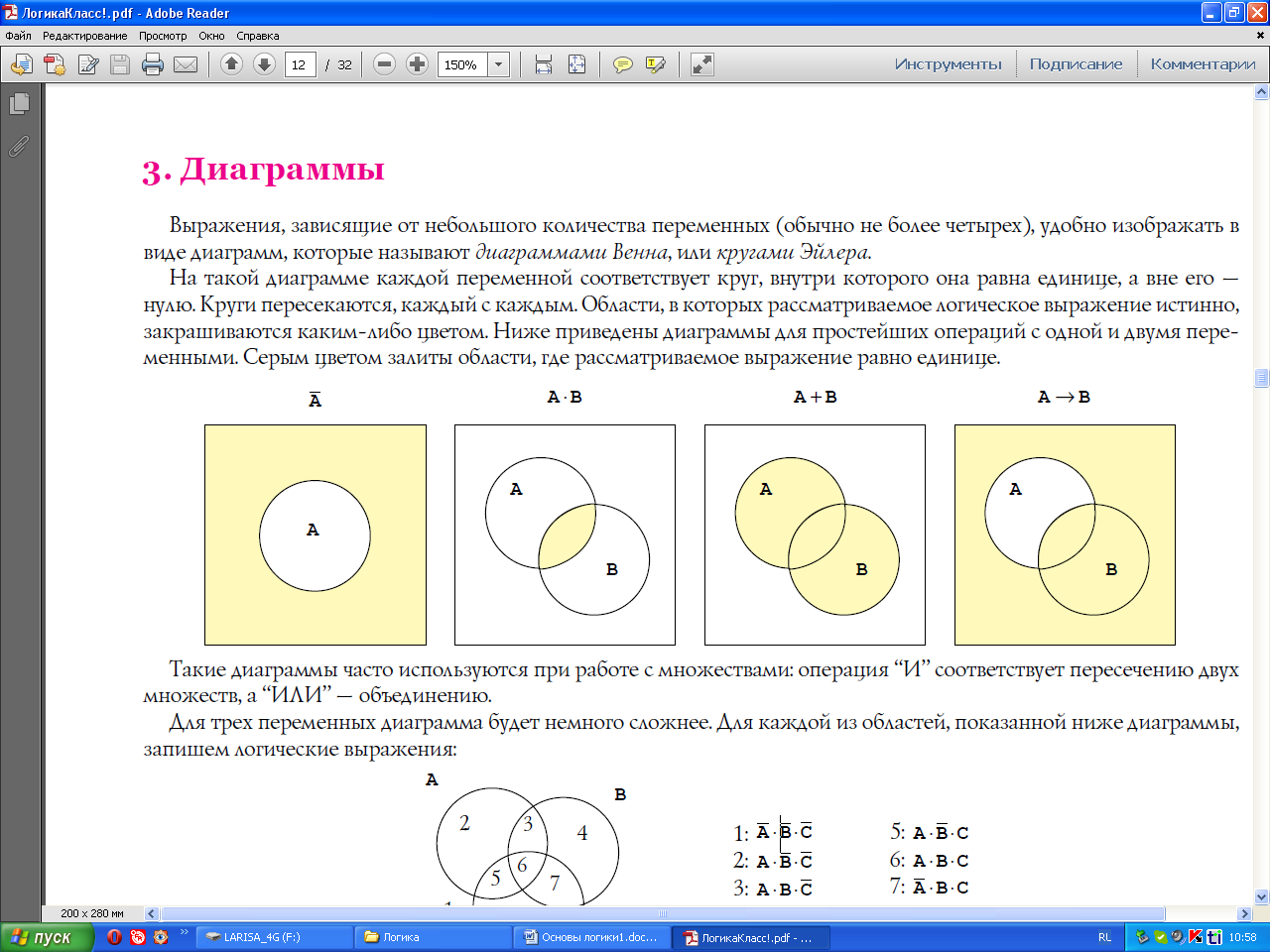
Такие диаграммы часто используются при работе с множествами: операция “И” соответствует пересечению двух множеств, а “ИЛИ” — объединению.

Для трех переменных диаграмма будет немного сложнее. Для каждой из областей, показанной ниже диаграммы, запишем логические выражения:

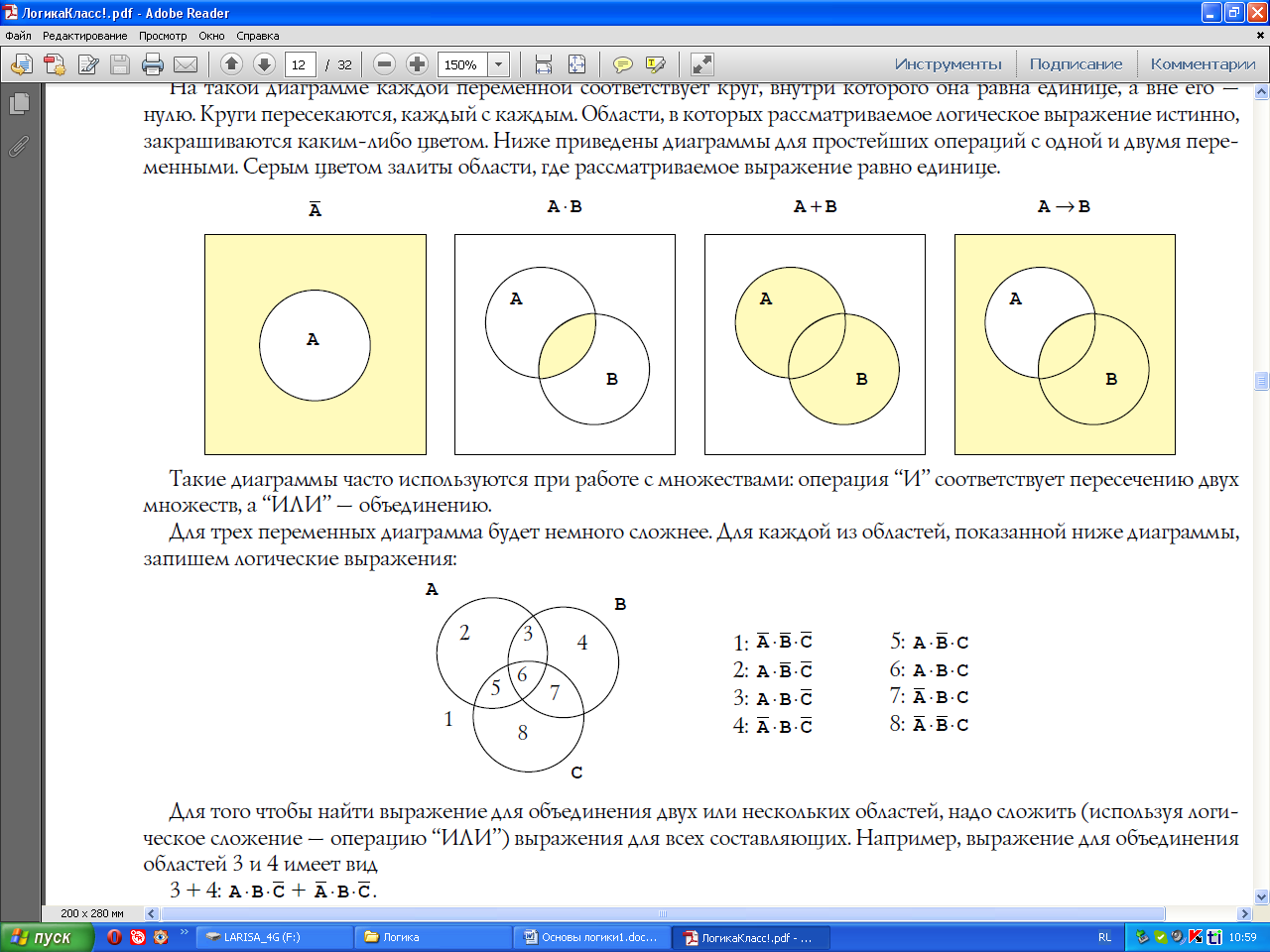
Для того чтобы найти выражение для объединения двух или нескольких областей, надо сложить (используя логическое сложение — операцию “ИЛИ”) выражения для всех составляющих. Например, выражение для объединения областей 3 и 4 имеет вид

3 + 4: + .

С другой стороны, можно заметить, что справедлива формула

3 + 4: .

Это означает, что логические выражения в некоторых случаях можно упростить.

Диаграммы удобно применять для решения задач, в которых используются множества, например, множества ссылок, полученных от поисковой системы в ответ на какой-то запрос. Рассмотрим такую задачу:

16. Известно количество ссылок, которые находит поисковый сервер по следующим запросам (здесь символ “&” обозначает операцию “И”, а “|” — операцию “ИЛИ”):

собаки 200

к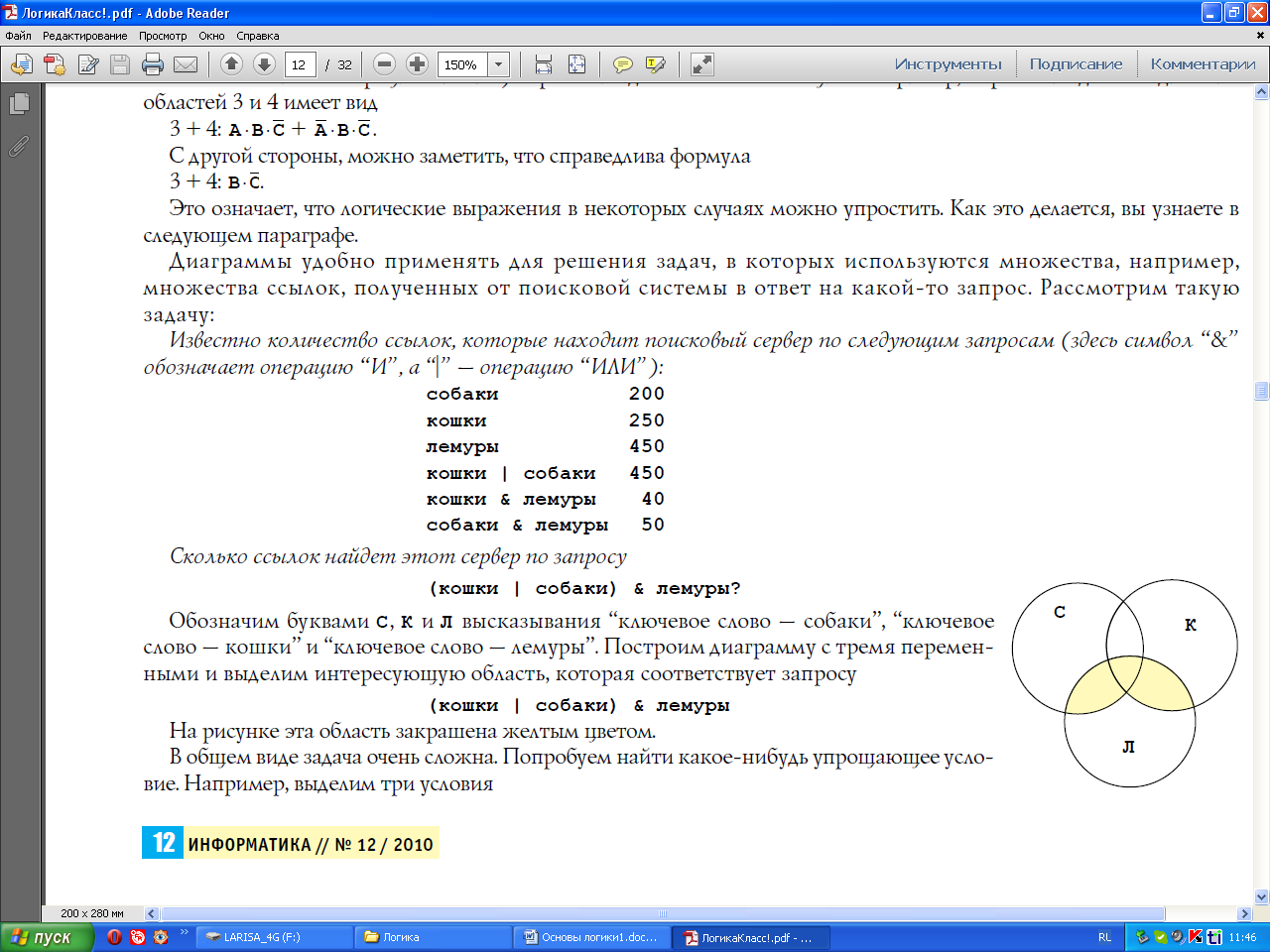 ошки 250

лемуры 450

кошки | собаки 450

кошки & лемуры 40

собаки & лемуры 50

Сколько ссылок найдет этот сервер по запросу (кошки | собаки) & лемуры?

Обозначим буквами С, К и Л высказывания “ключевое слово — собаки”, “ключевое слово — кошки” и “ключевое слово — лемуры”.

Построим диаграмму с тремя переменными и выделим интересующую область, которая соответствует запросу

(кошки | собаки) & лемуры

На рисунке эта область закрашена желтым цветом.

В общем виде задача очень сложна. Попробуем найти какое-нибудь упрощающее условие. Например, выделим три условия

собаки 200

кошки 250

к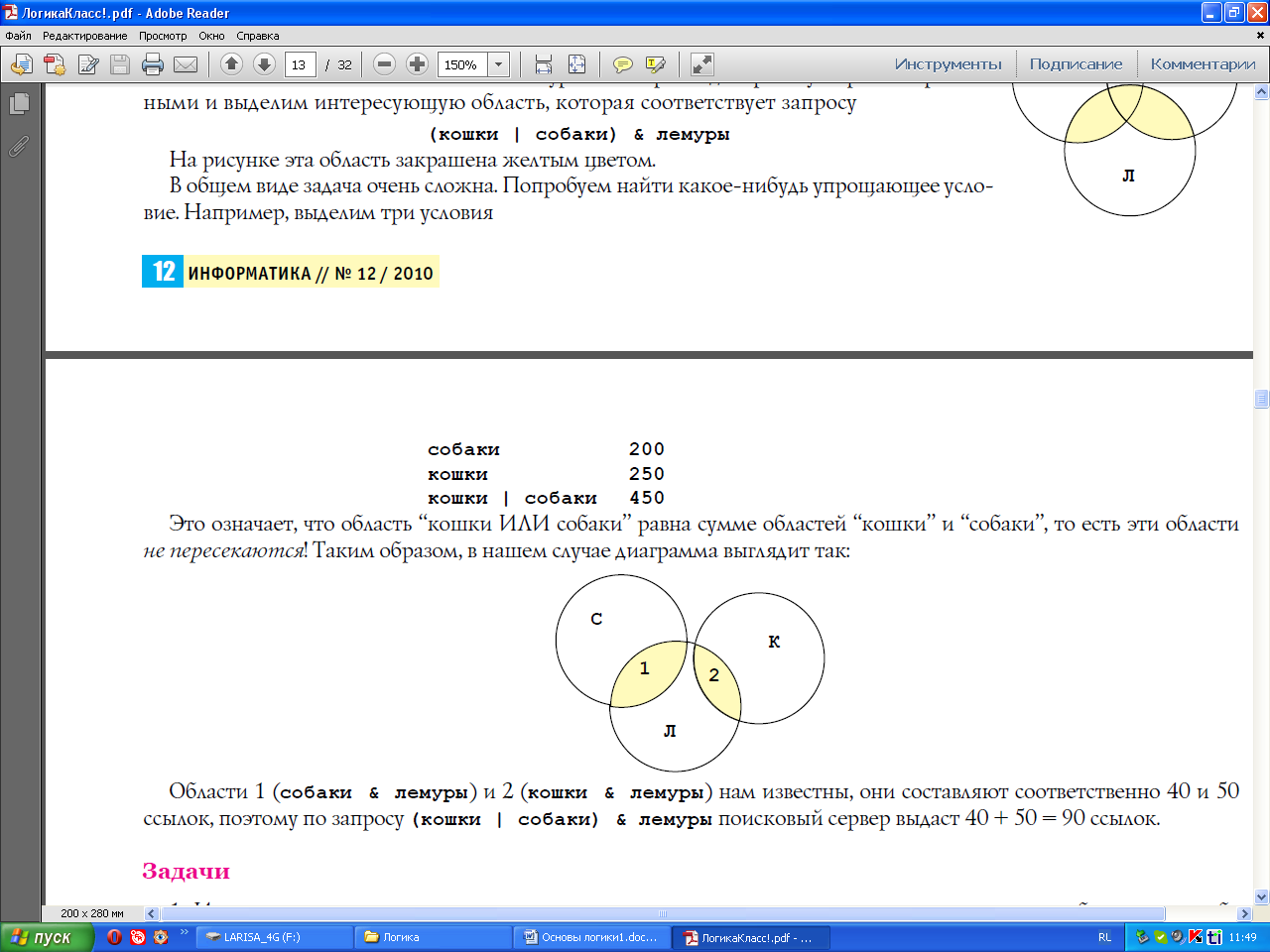 ошки | собаки 450

Это означает, что область “кошки ИЛИ собаки” равна сумме областей “кошки” и “собаки”, то есть эти области не пересекаются! Таким образом, в нашем случае диаграмма выглядит так:

Области 1 (собаки & лемуры) и 2 (кошки & лемуры) нам известны, они составляют соответственно 40 и 50 ссылок, поэтому по запросу (кошки | собаки) & лемуры поисковый сервер выдаст 40 + 50 = 90 ссылок.

17. Известно количество ссылок, которые находит поисковый сервер по следующим запросам:

собаки 250

кошки 200

лемуры 500

собаки & лемуры 0

собаки & кошки 20

кошки & лемуры 10

Сколько ссылок найдет этот сервер по запросу

кошки | собаки | лемуры?

(Ответ: 920)

18. Известно количество ссылок, которые находит поисковый сервер по следующим запросам:

собаки 120

кошки 270

лемуры 100

кошки | собаки 390

кошки & лемуры 20

собаки & лемуры 10

Сколько ссылок найдет этот сервер по запросу

кошки | собаки | лемуры?

(Ответ: 460)

3. Логические функции.

Любое составное высказывание можно рассматривать как логическую функцию F(x₁,x₂, …x_n), аргументами которой являются логические переменные x₁,x₂, …x_n- простые высказывания. Сама функция, и ее аргументы принимают только логические значения.

Для двух переменных существует 16 (2⁴) различных логических функций двух аргументов. Некоторые из них имеют свое название.

Аргументы		Функции
А	В	F1	F2	F3	F4	F5	F6	F7	F8	F9	F10	F11	F12	F13	F14	F15	F16
0	0	0	0	0	0	0	0	0	0	1	1	1	1	1	1	1	1
0	1	0	0	0	0	1	1	1	1	0	0	0	0	1	1	1	1
1	0	0	0	1	1	0	0	1	1	0	0	1	1	0	0	1	1
1	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1
		Ноль	Конъюнкция	Не импликация	А		В	Исключающее ИЛИ	Дизъюнкция	Не Или Стрелка Пирса	Эквиваленсия	Не В		Не А	Импликация	Не И Штрих Шеффера	Единица

Импликация (логическое следование).

Обозначение:

• в естественном языке соответствует обороту если …, то …;

• в алгебре высказываний обозначение ;

• в языках программирования обозначение Imp.

Импликация – это логическая операция, которая каждым двум простым высказываниям ставит в соответствие составное высказывание, являющееся ложным тогда и только тогда, когда условие (первое высказывание) истинно, а следствие (второе высказывание) ложно.

Таблица истинности

X	Y	X  Y
0	0	1
0	1	1
1	0	0
1	1	1

Свойства операции:

A  B  B  A

A  A = 1

A  0 =

A  1 = 1

0  A=1

1  A= A

Примеры:

19. Если сегодня четверг, то 2*2=5 (кроме четверга - истина)

20. Отец сказал сыну: «Если я получу премию, то куплю тебе велосипед».

21. Если белые медведи живут в Африке, то 2*2=5

22. Если три стороны одного треугольника равны трем сторонам другого треугольника, то такие треугольники равны.

23. Для того, чтобы треугольники были равны, необходимо, чтобы они были подобны.

24. Для того, чтобы были лужи, достаточно, чтобы пошел дождь. (Обратное неверно, потому что лужи могут возникнуть из за водопроводной аварии)

Упражнения

19. (12/ 6)  (12/3)

20. (15/ 6)  (15/3)

21. Определить истинность А: А  (4 – нечетное число)=1

22. Определить истинность А: (2 – четное число )  А=0

Эквивалентность (равнозначность).

Обозначение:

• в естественном языке соответствует обороту речи тогда и только тогда;

• в алгебре высказываний обозначение , ;

• в языках программирования обозначение Eqv.

Эквивалентность – это логическая операция, которая каждым двум простым высказываниям ставит в соответствие составное высказывание, являющееся ложным тогда и только тогда, когда оба исходных высказывания одновременно истинны или одновременно ложны.

Таблица истинности

X	Y	X  Y
0	0	1
0	1	0
1	0	0
1	1	1

Свойства операции:

A  B = B  A

 = А  В

A  0 =

A  1 = А

АА=А