Программа выполнения работы

1. Подготовить протокол работы, содержащий название работы, цель работы, схемы экспериментов и таблицы для записи результатов.

2. Пользуясь программой «Electronics Workbench» собрать схемы установок и выполнить измерения сопротивлений. Все установки состоят из различным образом соединенных резисторов и мультиметров, включенных в режиме измерения сопротивлений. Параметры элементов (сопротивления резисторов) указаны на схеме. Параметры мультиметра соответствуют принятым по умолчанию (ток омметра равен 0,01 мкА).

3. Выполнить расчеты сопротивлений схем и сравнить с измеренными значениями.

Порядок выполнения работы

1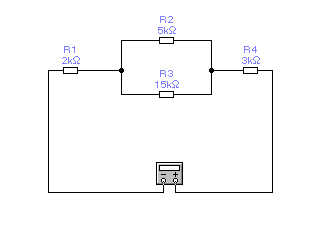 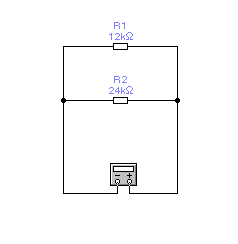. Собрать в программе Electronics Workbench схемы, изображенные на рис. 1.7, а.

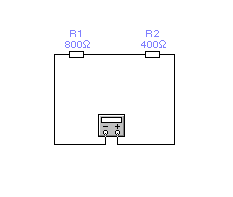
а)

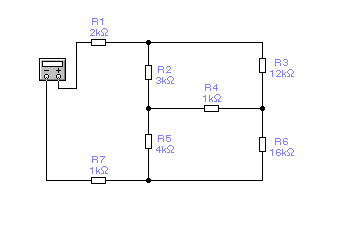
Рис. 1.7

2. Используя правила эквивалентных преобразований цепей, аналитически рассчитать эквивалентное сопротивление цепи относительно точек, к кото­рым подключен мультиметр.

3 . Включить схему и измерить эквивалентное сопротивление цепи. Сравнить результат измерения с результатом аналитического расчета (пункт 2).

4. Повторите пункты 1 - 3 для установок, изображенных на рисунках 1.7, б – 1.7, д.

5. Заполнить отчет. Отчет должен содержать титульный лист, цель работы, схемы исследуемых цепей, результаты эквивалентных преобразований це­пей со всеми промежуточными выкладками и результаты измерений эквива­лентных сопротивлений, выводы.

Контрольные вопросы

1. Какие преобразования электрических цепей называют эквивалентными? Для чего их применяют?

2. Как найти эквивалентные сопротивление, индуктивность, емкость для по­следовательно соединенных элементов?

3. Перечислите основные правила последовательного соединения.

4. Как найти эквивалентные сопротивление, индуктивность, емкость для па­раллельно соединенных элементов?

5. Перечислите основные правила параллельного соединения.

6. Как преобразовать треугольник сопротивлений в эквивалентную звезду? Как преобразовать звезду в эквивалентный треугольник?

Лабораторная работа №2 экспериментальная проверка законов ома и кирхгофа.

Цель работы: Экспериментально подтвердить справедливость законов Ома и Кирхгофа. Научиться составлять уравнения по законам Ома и Кирхгофа. Освоить методику расчета электрических цепей с использованием этих законов. Овладеть методикой построения потенциальной диаграммы.

Краткие теоретические сведения

Законы Ома и Кирхгофа являются основными законами, используемыми при расчетах электрических цепей. Они позволяют установить соотношения между э.д.с., напряжениями, токами и сопротивлениями в этих цепях.

Ток – это направленное движение заряженных частиц, как положительных, так и отрицательных. Количественно величина тока определяется скоростью изменения заряда, переносимого через поперечное сечение проводника

.

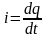Закон Ома выражает связь между током, напряжением и сопротивлением. Для участка цепи, представленного на рис. 2.1, согласно закону Ома ток прямо пропорционален напряжению, приложенному к этому участку и обратно пропорционален сопротивлению этого участка

.

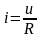Н апряжение, приложенное к точкам 1-2, представляет собой разность потенциалов между этими точками .

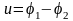Потенциалы точек могут быть определены относительно какой-либо точки цепи измерением с помощью вольтметра или расчетом, если известны значения э.д.с., и сопротивлений, а также величина и направление токов в ветвях. При расчете потенциалов точек необходимо учитывать, что на участке цепи, не содержащем э.д.с., ток течет от точки с большим потенциалом к точке с меньшим потенциалом. Следовательно, если направление обхода совпадает с направлением тока, то происходит уменьшение потенциала на величину падения напряжения на данном участке цепи, например,

.

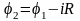При обходе против тока происходит увеличение потенциала на величину падения напряжения.

Если участок цепи содержит источник э.д.с. (рис. 2.2), то следует учитывать, что при переходе от отрицательного зажима источника э.д.с. к положительному потенциал повышается на величину э.д.с. источника. При переходе в обратном направлении потенциал понижается на величину э.д.с. источника независимо от направления тока, например,

.

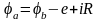
Следовательно, закон Ома для данного участка цепи запишется

.

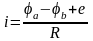Для замкнутой цепи, содержащей один источник э.д.с. (рис. 2.3), ток источника определится законом Ома для полной цепи

,

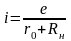
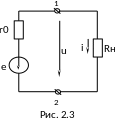где е – э.д.с. источника; r₀ – внутреннее сопротивление источника; R_н – общее сопротивление внешней цепи. Если известны ток в цепи и э.д.с. источника, внутреннее сопротивление можно рассчитать, исходя из внешней характеристики источника

.

Отсюда

,

где и – напряжение на зажимах источника.

Законы Кирхгофа состоят в следующем.

Первый закон Кирхгофа относится к узлам электрической цепи и характеризует баланс токов в них. Первый закон Кирхгофа формулируется следующим образом: алгебраическая сумма токов в узле электрической цепи равна нулю. При этом токи, направленные к узлу, берутся с одним знаком, например, с плюсом, а токи, направленные от узла с противоположным знаком.

Второй закон Кирхгофа относится к контурам электрической цепи и характеризует баланс напряжение в них. Второй закон Кирхгофа формулируется следующим образом: алгебраическая сумма э.д.с., действующих в замкнутом контуре электрической цепи, равна алгебраической сумме падений напряжения на элементах этого контура. При этом следует учитывать, что при совпадении направления обхода контура с направлением э.д.с. источника э.д.с. берется со знаком плюс, в противном случае – со знаком минус. Если направление обхода контура совпадает с направлением тока в элементе, то падение напряжения берется со знаком плюс, в противном случае – со знаком минус.