Лабораторная работа №1 экспериментальное подтверждение справедливости правил преобразования электрических цепей

Цель работы: экспериментально подтвердить справедливость правил преоб­разования пассивных электрических цепей. Получить практические навыки пре­образования электрических цепей.

Краткие теоретические сведения

Анализ электрических цепей часто может быть существенно упрощен пу­тем использования различных преобразований, которые позволяют заменить одни участки идеализированных цепей другими, более удобными для анализа.

Два участка идеализированной электрической цепи называются эквива­лентными, если при замене одного из этих участков другим токи и напряжения остальной части цепи не изменяются. Очевидно, эквивалентные участки имеют одинаковое число внешних выводов, причем токи этих выводов и напряжения между ними должны при преобразованиях оставаться неизменными. Преобра­зования электрических цепей, при которых некоторые участки цепи заменяются эквивалентными участками, также называются эквивалентными.

Если эквивалентность двух участков электрических цепей выполняется при любых значениях внешних воздействий, то такие участ­ки являются полностью эквивалентными. Если же эквивалентность двух участ­ков выполняется только при определенных значениях параметров внешних воздействий (например, при заданной частоте), то такие участки являются час­тично эквивалентными (эквивалентными при заданных условиях).

Эквивалентные преобразования электрических цепей основаны на экви­валентных (равносильных) преобразованиях соответствующих систем уравне­ний электрического равновесия. Соответственно изменяется и вид схемы цепи. На практике эквивалентные преобразования электрических цепей проводят пу­тем непосредственного преобразования схем по определенным правилам без составления систем уравнений электрического равновесия. При дальнейшем анализе систему уравнений электрического равновесия записывают уже для преобразованной цепи.

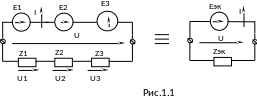
Последовательным соединением элементов называют такое соединение, при котором между элементами нет ответвлений (рис.1.1).

При последовательном соединении выполняются следующие правила:

1. через все элементы протекает один и тот же ток;

2. напряжение на последовательном участке цепи равно сумме напряжений на элементах этого участка

3. участок цепи, содержащий N последовательно соединенных комплекс­ных сопротивлений Z, может быть заменен одним комплексным сопротивлением Z_эк

.

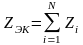В частности, для последовательных соединений двух резисторов (рис. 1.2, а), двух катушек (рис. 1.2, б) и двух конденсаторов (рис. 1.2, в) можно записать:

;

;

; .

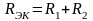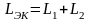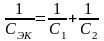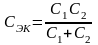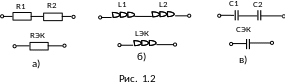
Параллельным соединением элементов (или ветвей) называют такое соединение, при котором несколько элементов (или ветвей) подключены к одной паре узлов.

Для параллельного соединения справедливы следующие правила:

1. напряжение на всех элементах одинаково;

2. общий ток параллельного участка равен сумме токов в ветвях;

.

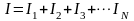3. участок цепи, содержащий N параллельно соединенных комплексных со­противлений Z_i (рис. 1.3), может быть заменен одним комплексным сопро­тивлением Z_эк:

.

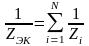
В частности, для параллельных соединений двух резисторов (рис 1.4, а), двух катушек (рис. 1.4, б) и двух конденсаторов (рис. 1.4, в) можно записать:

.

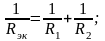
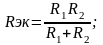
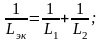
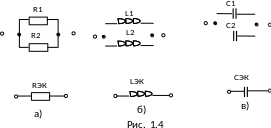
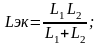
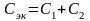Если преобразуемый участок цепи представляет собой смешанное со­единение комплексных сопротивлений, то для эквивалентных преобразований такого участка можно применять рассмотренные правила для последователь­ного и параллельного соединения, т.к. смешанное соединение представляет собой сочетание групп параллельно и последовательно соединенных элемен­тов. В многоэлементных электрических цепях со смешанным соединением иногда бывает невозможно сразу выделить участки с последовательным или параллельным соединением. В этом случае эквивалентное сопротивление всей цепи находят поэтапно, рассчитывая эквивалентные сопротивления отдельных участков, последовательно упрощая схему, свертывая ее.

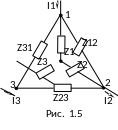
В некоторых случаях в электрических цепях существуют такие соединения элементов, которые не поддаются расчетам по методу свертывания, так как не содержат ни последовательно, ни параллельно соединенных элементов. Для того, чтобы найти эквивалентное сопротивление такой схемы применяют преобразование треугольника сопротивлений в эквивалентную звезду.

В приводимых ниже формулах приняты обозначения, введенные на ри­с. 1.5. Для преобразования треугольника в эквивалентную звезду можно воспользоваться формулами:

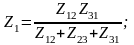
Для преобразования звезды в треугольник можно воспользоваться фор­мулами:

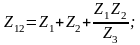
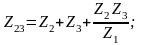
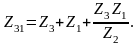
Иногда при эквивалентных преобразованиях удобнее пользоваться вы­ражениями не для сопротивлений, а для проводимостей.

Любая N-лучевая звезда может быть преобразована в эквивалентный N-угольник по формулам:

,

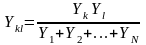где Y_kl - проводимость стороны N-угольника, соединяющей узлы k и l; Y₁, Y₂, ....Y_N- проводимости элементов, образующих лучи звезды. Обратное пре­образование полного N-угольника в N-лучевую звезду в общем случае невоз­можно.

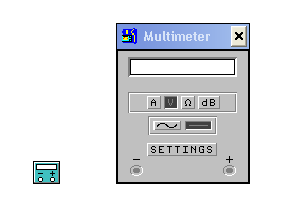
В программе Electronics Workbench имеется модель универсального из­мерительного прибора - мультиметра (рис. 1.6).

Мультиметр позволяет измерять следующие величины: среднеквадратичное значение синусоидально­го тока или напряжения, значение постоянного тока или напряжения, сопротивление цепи постоянному току и падение напряжения между двумя точками схе­мы, выраженное в децибелах. Мультиметр располагается на панели приборов. Для его использования следует переместить значок мультиметра (рис. 2.6, а) в нужное место схемы и выполнить необходимые электрические со­единения. Лицевая панель мультиметра (рис. 2.6, б) раскрывается после двойного щелчка левой кнопкой мыши по значку.

а) б)

Рис. 2.6

Все органы управления мультиметром размещены на лицевой панели. В верхней части панели расположен индикатор, где отображаются результаты измерений. Ниже расположены кнопки выбора режима работы, обозначенные символами: А - измерение тока (амперметр), V - измерение напряжения (вольтметр), Ω - измерение сопротивления (омметр) и dB - измерение разности потенциалов (напряжения) в децибелах (вольтметр с логарифмической шка­лой). Под кнопками выбора режима работы расположены кнопки выбора рода тока: переменного или постоянного, обозначенные соответственно волнистой и прямой линиями. Еще ниже расположена кнопка «SETTINGS», нажатие на ко­торую приводит к открытию диалогового окна, где можно задать параметры из­мерителей: внутренние сопротивления вольтметра и амперметра, измеритель­ный ток омметра и стандартный уровень напряжения для измерения разности потенциалов в децибелах. В нижней части лицевой панели расположены две клеммы внешних соединений прибора, обозначенные «-» и «+». При измерении постоянных токов или напряжений следует соблюдать полярность подключения прибора, при измерении переменных токов или напряжений и при измерении сопротивлений полярность подключения прибора значения не имеет. При из­мерении сопротивлений необходимо установить режим постоянного тока и сле­дить за тем, чтобы измеряемый участок цепи был обесточен.