Четвертая лекция Карты Карно

y=f(x1,x2), т.е. при изменении сигнала на входе, проис­ходит изменение сигнала на выходе. Теоретически сигнал мгно­венно изменяется на выходе, на самом деле существуют пере­ходные процессы.

Схема, в которой набор выходных переменных в каждый дискретный момент времени однозначно определяется по входно­му слову, поданному в тот же момент времени, называется ком­бинационной.

Для комбинационных схем результат обработки зависит только от комбинации входных сигналов и вырабатывается сразу же после появления энергии на входах.

Переходные процессы влияют на распределение информации, для устранения этого недостатка используют тактирование.

Примеры комбинационных схем:

(сумматоры, дешифраторы, компараторы, мультиплексоры...)

Устройство, входное слово которого в дискретные моменты времени определяется не только по входному слову, но и по его внутреннему состоянию, обусловленному его предшествующи­ми этапами работы, называется конечным автоматом.

Порядок синтеза

1. На основе технического задания составляется таблица истинности, где отражаются значения выходной функции в зависимости от комбинации входных.

X1	X2	X3	Y
0 0 0 0	0 0 1 1	0 1 0 1	0 1 1 1
1 1 1 1	0 0 1 1	0 1 0 1	0 0 1 0

2. Выделяем строки когда выходная функция равна 1.

3. Составляем карту Карно, которая отражает единичное значение выходной функции при заданных значениях входных аргументов.

X 1X2 X3	00	01	11	10
0		1	1
1	1	1

4. На карте Карно выделяем контура в которых выходная функция несет единичное значение, при чем:

А) число контуров должно быть минимум,

Б) число единиц входящих в контур максимум,

В) контура должны быть прямоугольной формы,

Г) карта Карно представляет сферу,

Д) одна и та же единица может несколько раз входить в различные контура,

Е) число единиц в контуре должно соответствовать 2ⁿ.

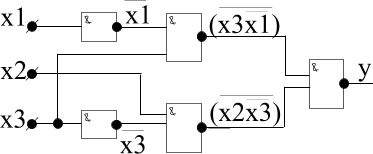
5. В минимальную дизъюнктивную нормальную функцию записываются те аргументы которые не меняют своего знака при обходе по контуру:

6. Для реализации схемы на элементах Шеффера или Пирса применяем теорему Де Моргана:

отрицание дизъюнкции равно конъюнкции отрицания

Теорема Котельникова

При преобразовании аналогового сигнала в цифровой без потери информации время выборки должно быть меньше или равно:

t_в=1/2f_в, где f_в – верхняя граничная частота спектра входного сигнала.

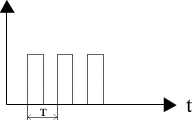, f=50МГц, T=0,02 мкс – продолжительность такта.

Например, чем больше f компьютера, тем быстрее он работает.

Синтез последовательностных схем

У последовательностных схем выходная функция зависит от значения выходной функции в предыдущий момент времени. Последовательностная схема на основе определения обладает обратной связью.

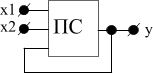
Для получения устойчивого положения используют ООС. При введение обратной связи часть выходной энергии подается на вход синтезируемой схемой и поддерживает значение выходной функции в устойчивом состоянии сколь угодно долго, если не отключать источник питания. Поэтому последовательностная схема обладает памятью. Основным устройством последовательного типа является триггерная схем.