2. Наращение процентов и инфляция.

Во всех выше рассмотренных примерах наращенные величины применялись по номиналу, т.е. не принималась во внимание реальная покупательная способность денег, однако инфляция является неотъемлемым элементом экономического развития и её следует учитывать при проведении финансовых операций. Изменение покупательной способности денег характеризуется с помощью индекса покупательной способности рубля. Обозначается I_пср. Этот индекс равен обратной величине индекса цен.

,

тогда реальная наращенная сумма денег с учётом её обесценивания будет равна

.

Если наращение производится по простой учётной ставке, то реально наращенная сумма с учётом инфляции равна:

.

Из этого выражения можно увидеть, что увеличение наращенной суммы денег – сохранение покупательной способности имеет место, если

При наращении по сложным процентным ставкам реальная наращенная сумма определяется:

.

В обеих формулах I_p – это индекс цен за весь период наращения. Обычно I_p определяется на месяц и тогда I_p за какой – то срок (несколько месяцев) определяется как I_p =П (i_pi + 1),

П – произведение;

i_pi – индекс цен за i – й месяц.

Пример:

На сумму 15000 р. В течение трех месяцев начисляется % по ставке 30% годовых. Ежемесячно инфляция - 3% . Определить реальную погашаемую сумму.

,

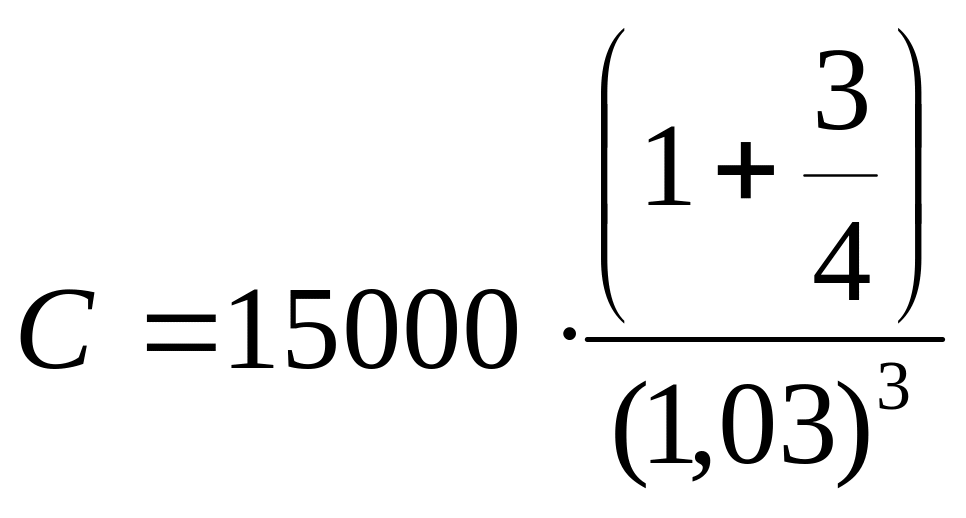С = 14752.

Ответ:14752.

2.1. Консолидация платежей

В практической деятельности возникает необходимость изменения условий контракта на предмет объединения (консолидации) нескольких платежей или замена единовременного платежа рядом последовательных с разными сроками. Условным требованием является финансовая эквивалентность платежей. Общим методом решения таких задач является построение уравнения эквивалентности, что означает при объединении платежей, приведённых к одной дате, их сумма приравнивается к новому обязательству. Уравнение эквивалентности при применении простых процентных ставок имеет вид:

t_j = n₀ +n_j;

n₀ – срок консолидации платежей;

n_j – срок объединяемых платежей;

n₀ > n_j.

Пример:

Решено консолидировать три платежа по срокам: 17 мая, 17 июня, 17 августа. Соответствие суммы 10, 20, 30 тыс. руб. Срок консолидации платежей 31 августа. Определить сумму консолидированного платежа, если годовая процентная ставка 10%.

t₁ = 106; t₂ = 75; t₃ = 31 - 17 = 14.

S₀ = 10⁴ (1 + 106/360*0,1) + 20000(1 + 75/360*0,1) + 30000(1 + 14/360*0,1) = 60827,76

Ответ: 60827,76

2.2 Методы составления планов погашения обязательств

Современные финансово-кредитные операции часто предусматривают не отдельные или разовые платежи, а какую – то их последовательность. Такие последовательности платежей называется потоками платежей, а их отдельные элементы – членами потока.

Поток платежей, все члены которого одинаковой величины, а временные интервалы между платежами одинаковы, называются финансовыми рентами, или аннуитетом. Например, выплата в рассрочку страховой премии, процентов по облигациям и т.д. По количеству выплат (членов ренты) в течение года ренты делят на годовые (выплаты раз в год) и р – срочные (выплаты р – раз в год). По количеству начисления процентов на протяжении года различают ренты с начислением m раз в году и с непрерывным начислением. Если платежи осуществляются в конце периодов, то такие ренты называется обыкновенными, или постнумерандо, если платежи производятся в начале периодов, то такая рента называется пренумерандо.