9.7. Практическая часть

9.7.1 Оптимальный размер заказа

1. На фирме используется 400 единиц материала в месяц, стоимость каждого заказа равна 200 тыс. руб., стоимость хранения каждой единицы материала – 10 тыс. руб.

Ответьте на следующие вопросы:

1. Чему равен оптимальный размер заказа?

1. Сколько заказов следует делать в месяц?

2. Как часто необходимо делать каждый заказ?

При решении используются формулы модели Уилсона.

Р е ш е н и е:

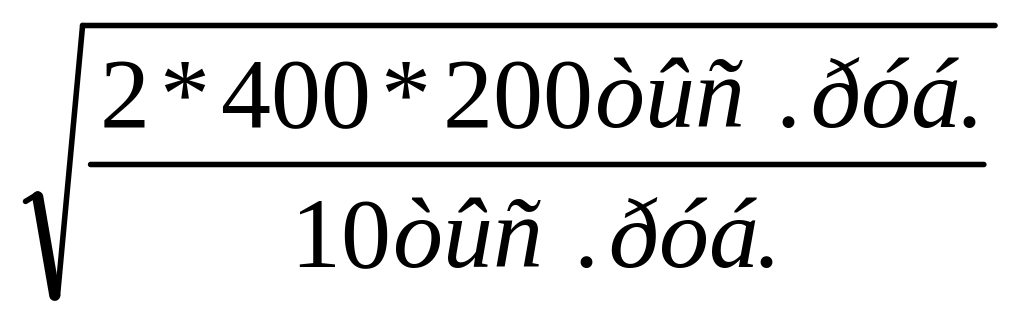1. = 127 шт.

2. 400 шт. / 127 шт. = 3 (заказа в месяц).

3. 30 дней / 3 раза = каждые 10 дней.

9.7.2 Управление запасами

2. Магазин продает в среднем в месяц 150 единиц товара. Каждый размещаемый заказ (заказанное одновременно количество товара) составляет 300 единиц товара. Стоимость каждой единицы товара равна 5 тыс. руб., стоимость одного заказа – 10 тыс. руб., стоимость хранения – 10 % от капиталовложений в запасы. Уровень процентной ставки составляет 20 %, налоговых выплат – 40 %.

О п р е д е л и т е:

1. капиталовложения в запасы;

2. годовую стоимость заказа;

3. годовую стоимость капиталовложений в запасы;

4. альтернативную стоимость капиталовложений;

5. полную нетто-стоимость запасов (за вычетом покупной цены).

Р е ш е н и е:

1. 150 шт.*5 тыс. руб. = 750 тыс.руб.

2. (150 шт.*12) / 300 * 10 тыс. руб. = 60 тыс.руб.

3. 750 тыс. руб.*0,1 = 750 тыс.руб.

4. 750 тыс. руб. * 0,2 = 150 тыс. руб.

5. (100 % – 40 %) / 100 % * (60. тыс. руб. + 75 тыс. руб.) + 150 тыс. руб. = = 231 тыс. руб.

3. Открытое акционерное общество «Ротор» – дистрибьютор воздушных фильтров розничным магазинам. Оно покупает фильтры у нескольких производителей. Фильтры заказываются партиями по 100 шт., и каждый заказ стоит 40 руб. Розничные магазины предъявляют спрос на 20 000 фильтров в месяц, а удельные затраты по содержанию запасов – 10 коп. на фильтр в месяц.

а. Каков оптимальный объем заказа при таком большом размере партий?

б. Каков был бы оптимальный размер заказа, если бы удельные затраты по содержанию запасов были бы 5 коп. в месяц?

в. Каков был бы оптимальный размер заказа, если бы стоимость выполнения заказа была 10 руб.?

Р е ш е н и е:

а. Q* =

Затраты по содержанию запасов = 0,10 руб. *1 000 = 100 руб. Оптимальный размер заказа будет равен 4 000 фильтров, что представляет собой 5 заказов в месяц.

б. Q* =

Поскольку размер партии 1 000 фильтров, компания будет заказывать 6 000 фильтров каждый раз. Чем ниже затраты по содержанию запасов, тем относительно более важной становится стоимость выполнения заказа и тем больше оптимальный размер заказа.

в. Q* =

Чем меньше стоимость выполнения заказа, тем относительно более важными становятся затраты по содержанию запасов и тем меньше оптимальный размер заказа.

4. Чтобы сократить стартовые издержки, предприятие «Транзит» может сделать пробеги своих машин более длинными. Приблизительно подсчитанные сбережения от возросшей эффективности равны 260 000 руб. в год. Однако оборачиваемость запасов сократиться с 8 раз в год до 6. Годовая себестоимость реализованной продукции составляет 48 млн. руб. Следует ли компании поощрять введение нового плана производства, если требуемая норма прибыли на капитал, вложенный в запасы – 15%.

Р е ш е н и е:

Запасы после изменения = 48 млн. руб. / 6 = 8 млн. руб.

Нынешние запасы = 48 млн. руб. / 8 = 6 млн. руб.

Дополнительные запасы = 2 млн. руб.

Альтернативные издержки = 2 млн. руб. 15 = 300 000 руб.

Альтернативные издержки больше, чем экономия. Следовательно, не нужно принимать новый производственный план.

5. Объем продаж магазина – 500 пакетиков супа в год. Величина спроса равномерна во времени. Закупочная цена пакетика – 2 $. За один заказ продавец должен заплатить 10 $. Время поставки – 12 рабочих дней (в неделе 6 дней). По оценкам специалистов издержки хранения составляют 20 % от среднегодовой стоимости запасов. Сколько пакетов владелец магазина должен взять за раз, чтобы минимизировать затраты.

Р е ш е н и е:

1. Стоимость одного заказа = 10 $;

стоимость хранения одного пакетика = 0,2 *2 $ = 0,4 $.

Q_опт = = 158 пакетов;

Количество заказов = 500 / 158 = 3,16 зак. / год.

2. Периодичность заказа = Q_опт / Спрос = 158 / 500 = 0,316 г. = 15,8 недель = 94,8 дня.

3. Поскольку время поставки составляет 12 рабочих дней, то заказ производится на 2 недели до истощения запасов.

Уровень повторного заказа = еженедельный расход*2 недели = (158/15,8)*2 = 20 шт.

4. Стоимость обслуживания запасов = (Стоимость закупки + Стоимость хранения) = 10*(500/158) + 0,4*(158/2) = 63,2 $.

Общая годовая стоимость запасов = Стоимость обслуживания + Стоимость товара = 63,2 + 500*2 = 1 063,2 $.

Предположим, что производятся закупки не по 158, а по 160 шт. тогда стоимость обслуживания запасов составит:

10*(500/160) + 0,4*(160/2) = 63,25 $ ( > 63,2, но потери небольшие).

При объеме заказов 200 шт. стоимость обслуживания запасов:

10*(500/200) + 0,4*(200/2) = 65 $ ( > 63,2, но потери небольшие).

При объеме заказа 140 шт. стоимость обслуживания запасов:

10*(500/140) + 0,4*(140/2) = 63,7 $ ( > 63,2, но потери возрастают быстрее).

Следовательно, желательнее увеличивать оптимальный размер заказа, так как кривая стоимости обслуживания имеет более пологий вид (см. теорию).

6. Некоторой фирме необходимо иметь в составе 1 000 человек. Увольняются с работы в среднем 150 человек в год. Люди должны пройти обучение, стоимость которого 25 000 руб. Каждому человеку, который прошел обучение, но еще не работает, должны платить по 500 руб. в месяц. Надо определить сколько человек надо принимать на курсы и как часто их организовывать. Какова общая переменная стоимость обучения и принятия людей?

Р е ш е н и е:

1. Стоимость обучения («одного заказа») = 25 000 руб.; годовые выплаты прошедшим обучение, но не работающим сотрудникам («стоимость хранения единицы запасов») = 500*12 = 6 000 руб.; необходимое число новых сотрудников («объем спроса») = 150 чел.

2. Рассчитаем сколько человек надо принимать на курсы по формуле оптимального размера заказа:

Q = = 35 человек;

Число курсов в год = 150/35 = 4,3.

3. Общая переменная стоимость обучения и принятия людей = 25 000*4,3 + (6 000/4,3)*(35/2) = 131 918,6 руб.

7. Компания ежегодно продает 45 000 мешков удобрений. Оптимальный резервный запас (имеющийся у компании с самого начала) равен 2 000 мешков. Каждый мешок обходится компании в 1 долл., издержки хранения составляют 20 %, а размещение заказа у поставщиков компании обходится в 20 долл.

а. Каков оптимальный размер заказа?

б. Каков максимальный запас удобрений?

в. Каким будет средний запас компании?

г. Как часто компания должна размещать заказы?