Плоскость и прямая в пространстве
Обобщением уравнения прямой на плоскости является уравнение плоскости в пространстве
Ax+By+Cz+D=0.
обобщением которого, в свою очередь, является уравнение гиперплоскости в n-мерном пространстве, рассматриваемое в прикладных математических курсах.
Различные виды уравнения плоскости в пространстве:
1) уравнение
прямой, перпендикулярной данному вектору
и проходящей через данную точку
(рис. 20)
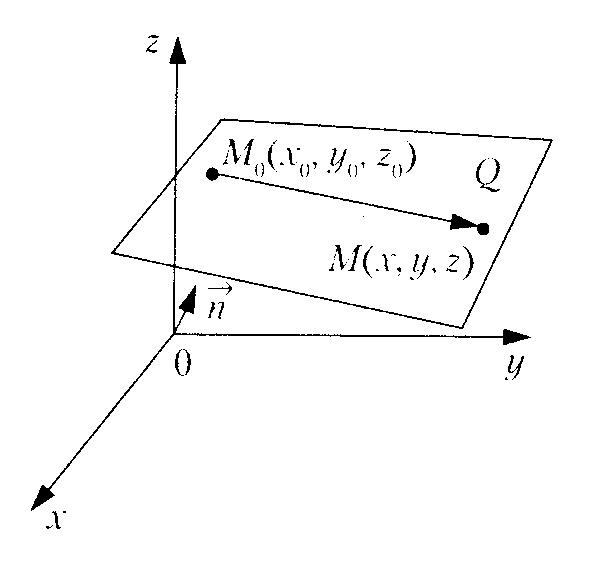
Рис. 20.
2) Общее уравнение плоскости
Ax+By+Cz+D=0,
при этом – вектор нормали (перпендикуляра) к плоскости.
Некоторые частные случаи общего уравнения плоскости:
1) плоскость, проходящая через начало координат
Ax+By+Cz=0 (D=0);
2) плоскость, параллельная оси Ox (Oy, Oz):
By+Cz+D=0 (Ax +Cz+D=0, Ax+By+D=0);
3) плоскость, параллельная плоскости Oxy (Oxz, Oyz);
Cz+D=0 (By +D=0, By +D=0);
4) плоскость Oxy (Oxz, Oyz):
z=0 (y=0, x=0).
Условие параллельности двух плоскостей
.
Условие перпендикулярности двух плоскостей
.
Пример. Составить уравнение плоскости, проходящей через точку M(1;-2;3) и:
а) перпендикулярной
вектору
;
б) параллельной плоскости 3x-4y+5z+6=0;
в) точку
и параллельной оси Oy.
Решение.
а) 3(x-1)-4(y+2)+5(z-3)=0 или 3x-4y+5z-26=0;
б) плоскость Ax+By+Cz+D=0 параллельна плоскости 3x-4y+5z+6=0, если
,
при коэффициенте пропорциональности,
равном 1, A=3,
B=-4,
C=5,
тогда получим
уравнение 3x-4y+5z+D=0;
D найдем, используя координаты точки M(1;-2;3):
3*1-4*(-2)+5*3+D=0, D=-26.
Окончательное уравнение 3x-4y+5z-26=0.
в) так как плоскость параллельна оси Oy, то в ее уравнении коэффициент В=0, т.е. уравнение плоскости имеет вид Ax+Cz+D=0. Используя координаты данных точек, получим:
,
.
Окончательно:
.
Различные виды уравнения прямой в пространстве
1) прямая как линия пересечения двух плоскостей
2) канонические
уравнения прямой, проходящей через
данную точку
с направляющим вектором
3) уравнение
прямой, проходящей через две данные
точки
и
.
Условия параллельности и перпендикулярности, углы
1. Пусть
даны две прямые
с направляющими векторами
и
:
угол между двумя прямыми
;
условие параллельности прямых в пространстве
;
условие перпендикулярности прямых в пространстве
.
2. Даны прямая и плоскость Ax+By+Cz+D=0:
угол между прямой и плоскостью
условие параллельности прямой и плоскости
Am+Bn+Cp=0
условие перпендикулярности прямой и плоскости
.
Пример.
Составить
уравнение плоскости, проходящей через
точку M(2;0;1)
и прямую
.
Решение. Используем уравнение плоскости, проходящей через точку
A(x-2)+By+C(z-1)=0.
Направляющий
вектор прямой
и нормальный вектор плоскости
перпендикулярны,
следовательно,
A+2B-C=0.
Точка A(1;-1;-1) лежит на прямой, следовательно, и на плоскости
A(1-2)+B(-1)+C(-1-1)=0 или –A-B-2C=0.
Решая систему,
получим A=-5C; B=3C.
Тогда
(-5(x-2)+3y+(z-1))С=0 или 5x-3y-z-9=0 .
1
Угол
получается при повороте прямой с
к прямой с
против часовой стрелки.