2.1. Вопросы для самопроверки

1. Поясните смысл величин, входящих в канониче­ские уравнения метода перемещений, а также смысл самого уравнения.

2. Как проверить окончательную эпюру моментов при расчете методом перемещений или смешанным методом?

3.Поясните смысл теоремы о взаимности реакций.

_4.Поясните теорему о взаимности коэффициентов

2.2. Расчетое задание №2. Расчет рамы методом перемещений

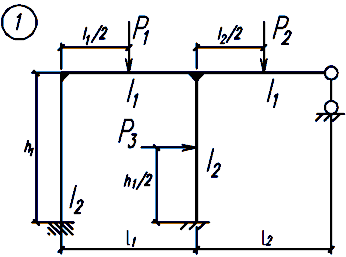
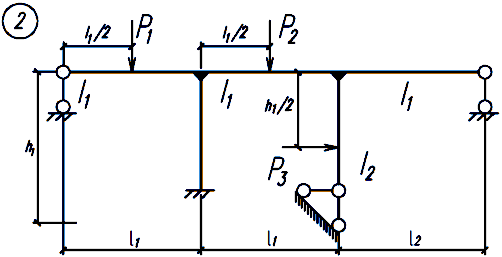
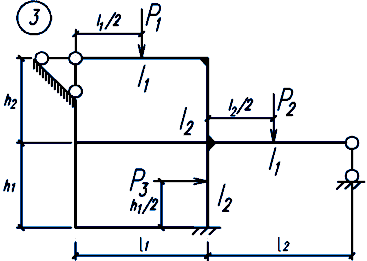
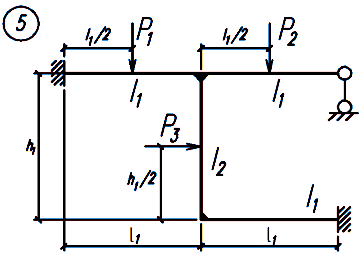
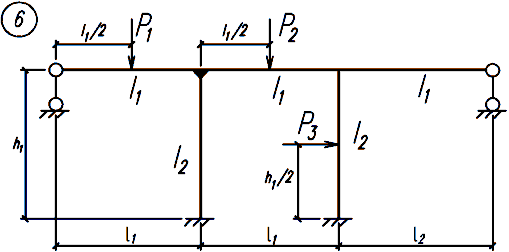
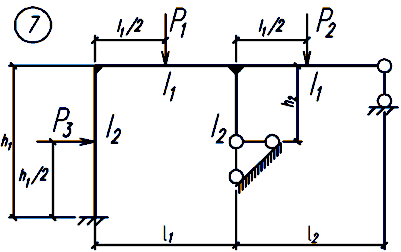
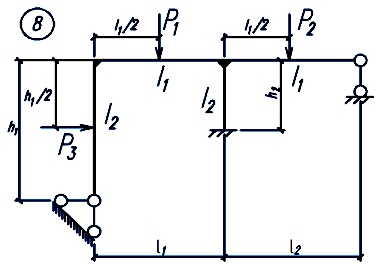
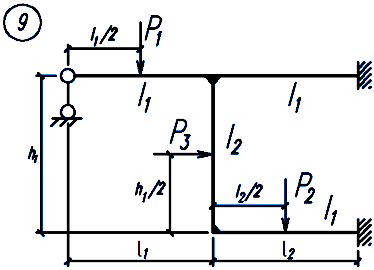
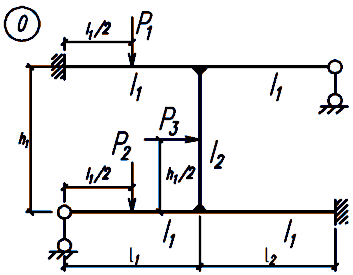
Задание. Для заданной статически неопределимой рамы (рисунок 18), с выбранными по шифру из таблицы 2 размерами и нагрузкой, требуется построить эпюры изгибающих моментов, поперечных и продольных сил.

Таблица 2

Первая цифра шифра	l1, м	l2, м	Вторая цифра шифра	h1 м	P1	P1	P1	Последняя цифра шифра (№ схемы)	h2 м	l1:l2
					Т
1	4	6	1	3	4	0	0	1	0	1:2
2	5	5	2	4	0	4	0	2	0	2:1
3	6	4	3	5	0	0	4	3	5	2:3
4	3	3	4	9	5	0	0	4	6	3:2
5	7	8	5	6	0	5	0	5	0	1:3
6	8	7	6	7	0	0	5	6	0	3:1
7	9	10	7	8	6	0	0	7	9	3:4
8	10	9	8	2	0	6	0	8	10	4:3
9	12	2	9	12	0	0	6	9	0	4:1
0	2	12	0	10	7	0	0	0	0	1:4

Рисунок 18

Методические указания

Решению задачи должно предшествовать изучение темы 2.

При выборе основной системы метода перемещений необходимо учитывать, что линейные связи должны быть поставлены не только по направлению возможных линейных перемещений, но и для устранения мгновен­ной изменяемости системы, образованной после поста­новки шарниров во все узлы (включая опорные).

При построении единичных и грузовых эпюр момен­тов используются таб-

лицы реакций, имеющиеся в учеб­никах по строительной механике (таблица 3).

Прежде чем приступать к подсчету коэффициентов канонических уравнений, необходимо значения ординат на всех единичных эпюрах выразить через какую-либо одну жесткость (ЕI₁ или ЕI₂). Удобно также перейти к погонным жесткостям стержней (i=EI:l). При опре­делении коэффициентов следует внимательно следить за их знаками.

Решение канонических уравнений необходимо про­верить путем подстановки найденных значений неиз­вестных в исходные уравнения.

После определения значений неизвестных рекомен­дуется построить окончательную эпюру момен­тов М по формуле:

(5)

В формуле (5) знаки ординат изгибающих моменнтов грузовой М_р и единичных принимаются по условному правилу, неизвестные Z₁….Z_n подставляются в формулу (5) со своим знаком.

Окончательную эпюру изгибающих моментов М необходимо проверить, используя:

- ста­тическую проверку (рассматривая равновесие узлов рамы и рамы в це­лом);

- деформационную проверку, которая выполняется как в методе сил. Для последней проверки необходимо выбрать основную систему метода сил и построить хотя бы одну единичную эпюру, которую следует «перемножить» с окочательной эпюрой мо­ментов.

Результат деформационной проверки должен быть равен нулю или быть близким к нулю (из-за неточ­ности в подсчетах- округлениях), при этом разница между положи­тельными и отрицательными слагаемыми, отнесенная к боль-шему из них, не должна превышать 3%.

Эпюру поперечных сил необходимо строить по эпюре мо­ментов так же,

как и в методе сил. Эпюра продольных сил строится как в методе сил.