1.1. Вопросы для самопроверки

1. Достоинства и недостатки статически неопределимых систем.

2. Определение числа лишних неизвестных в статически неопределимых систе­мах.

3.Выберите несколько основных систем в статически неопределимой раме и укажите лишние неизвестные.

4.Объясните смысл отдельных членов и всего уравнения:

5.Почему при деформационной проверке окончатель­ной эпюры момен-тов путем перемножения ее с одной из единичных эпюр или суммарной единичной эпюрой, должен получиться нуль?

6.Почему в пределах замкнутого контура рамы должно соблюдаться условие:

7.В чем заключается преимущество группировки неизвестных при расчете симметричных рам.

1.2. Расчетое задание 1. Расчет рамы методом сил

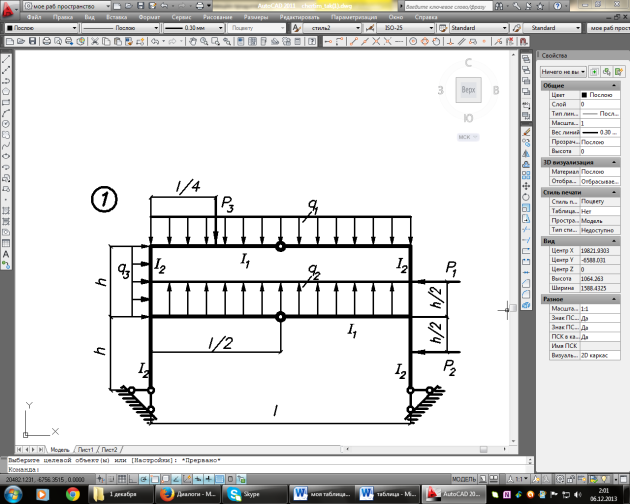
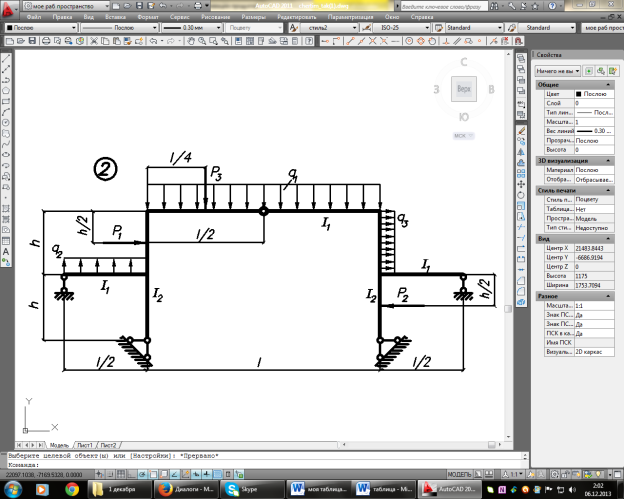
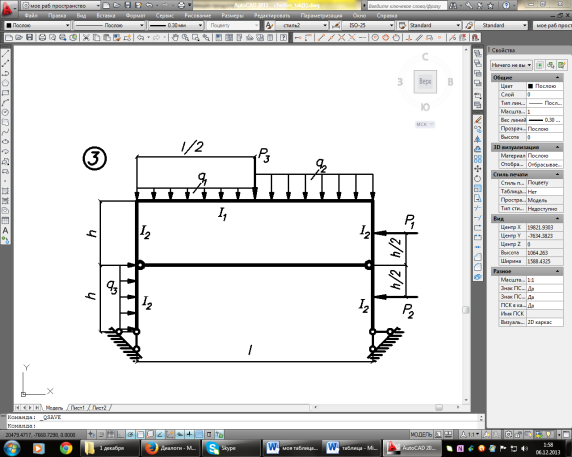
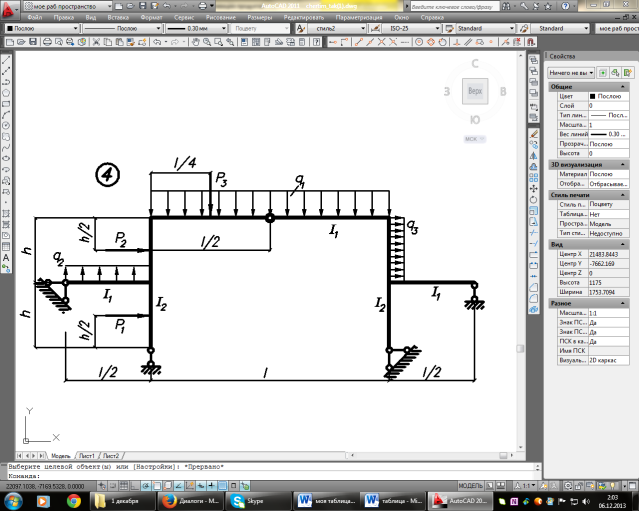
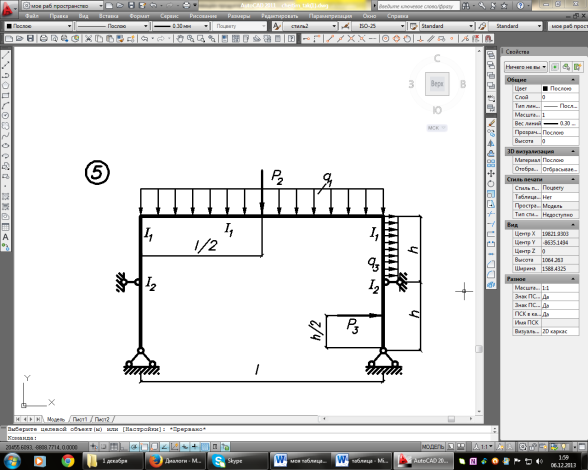
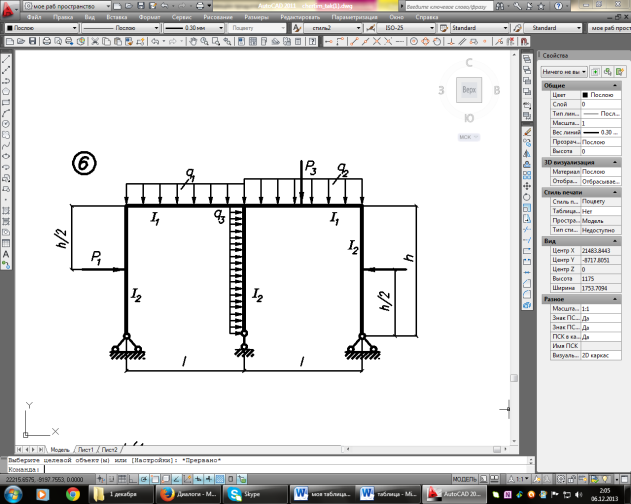
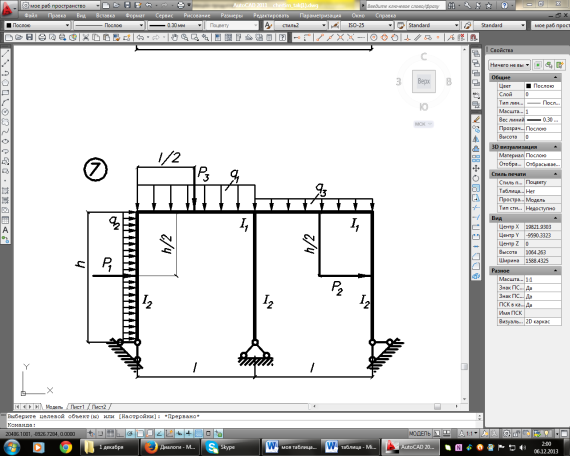
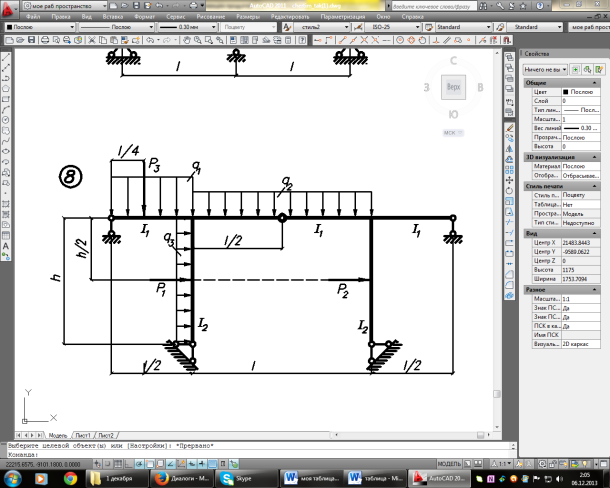
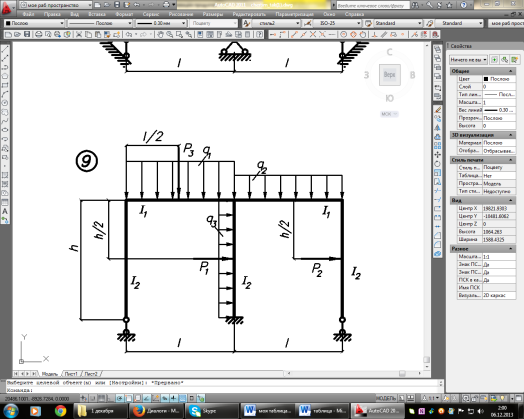
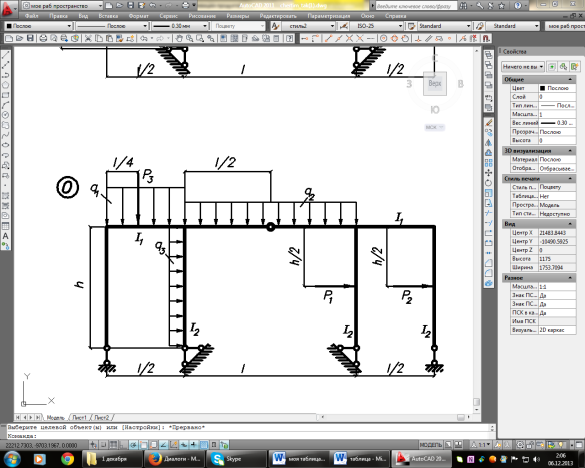
Задание. Для рамы (рисунок 1), с выбранными по шифру из таблицы 1 размерами и нагрузкой, требуется:

а) построить эпюры изгибающих моментов, попереч­ных и продольных сил;

б) проверить правильность построенных эпюр.

Методические указания

Решению задач должно предшествовать изучение темы «Расчет рамы методом сил»

Для упрощения расчета рекомендуется принимать для симметричных рам сим­метричную основную систему. Можно применить раз­ложение внешней нагрузки на симметричную и кососимметричную.

Рисунок 1

При построении единичных и грузовых эпюр орди­наты надо откладывать со стороны растянутых воло­кон, а при их «перемножении» не забывать о правиле знаков и разных жесткостях. Определив значения коэффициентов и сво- бодных членов, рекомендуется про­извести их проверку путем подсчета интегралов (по Верещагину):

,

где . Результат должен совпадать с суммой

Проверка правильности определения грузовых членов выполняется по формуле

Таблица 1

Первая цифра шифра	P1	P2	P3	l, м	Вторая цифра шифра	q1	q2	q3		h, м		Последняя цифра шифра (№ схемы)		l1: l2
	Т					Т/м
1	4	0	0	8	1	0	2	0		10		1		1:2
2	0	5	0	12	2	0	0	2		8		2		2:3
3	0	0	6	9	3	0	0	4		6		3		1:3
4	5	0	0	10	4	4	0	0		9		4		1:3
5	0	6	0	7	5	0	2	0		4		5		2:3
6	0	0	4	6	6	0	0	1		5		6		1:3
7	6	0	0	5	7	2	0	0		7		7		2:1
8	0	4	0	11	8	0	1	0		11		8		3:2
9	0	0	5	4	9	0	0	4		12		9		3:4
1 0	4	0	0	13	0	1	0	0		13		0		1:2

Решив систему уравнений, полученные значения не­известных подставляем в выражение для определения результирующих значений изгибающих моментов, умножая ординаты каж­дой единичной эпюры на соответствующее значение неизвестного. Тогда момент в любой точке исходной системы будет опре­деляться формулой

(2)

В формуле (2) знаки ординат изгибающих моменнтов грузовой М_р и единичных принимаются по условному правилу, неизвестные Х₁….Х_n подставляются в формулу (2) со своим знаком.

Окончательная эпюра изгибающих моментов M (для заданной системы) должна быть обя­зательно проверена путем «умножения» ее на любую из единичных эпюр или на сум­марную эпюру . Результат перемножения эпюр должен быть равен нулю или быть близким к нулю (из-за неточ­ности в подсчетах). При этом разница между положи­тельными и отрицательными слагаемыми, отнесенная к большему из них, не должна превышать 3%.

Построение эпюры поперечных сил (по эпюре мо­ментов) необходимо сопровождать расчетами. При этом особое внимание надо уделить правилу знаков и уча­сткам с криволинейным очертанием эпюры момен­тов. Знаки ординат эпюры поперечных сил опреде­ляются по правилам, принятым в курсе сопротивления материалов (при возрастании момента поперечная си­ла положительна). При построении эпюры моментов со стороны растянутых волокон возрастание момента будет характеризоваться наклоном вниз (слева — на­право). Можно записать следующее правило для определения знаков поперечной силы: Поперечная сила на участке считается положительной, если ось стержня совмещается с касательной, проведенной к эпюре изгибающих моментов на острый угол по часовой стрелке.

На участках, где эпюра моментов прямолинейна, значение Q определяется как тангенс угла наклона эпюры М. На криволинейных участках эпюры М по­строение эпюры Q производится по формуле

или Q^лев= ± + qℓ∕ 2*cosφ;

Q^прав= ± - qℓ∕ 2*cosφ, (3)

где φ – угол наклона стержня по отношению горизонтальной или вертикальной

оси; если распределенная нагрузка является поперечной по отношению

к рассматриваемому стержню, то φ=0; l – длина участка.

Эпюра N строится по эпюре поперечных сил путем вырезания узлов (как принято при расчете ферм), на­чиная с узла, в котором количество неизвестных про­дольных сил не превышает двух. При вырезании каж­дого узла необходимо учитывать, что положительная поперечная сила вращает узел по ходу часовой стрел­ки, а отрицательная — против.

После построения всех эпюр необходимо провести полную проверку, рассмотрев равновесие рамы це­ликом.