3.1. Вопросы для самопроверки

1. В чем состоит энергетический критерий потери устойчивости?

2. Поясните последовательность определения критиче­ской силы при расчете рам методом перемещений.

3. Какие требования предъявляются к основной си­стеме метода перемещений при расчете рам на устойчивость?

3.2. Расчетное задание 3. Расчет рамы на устойчивость

методом перемещений.

Задание. Для статически неопределимой рамы (рисунок 42), с выбранными по шифру из таблице 4 разме­рами и нагрузкой, требуется:

1.Определить значения кри­тических сил, используя метод перемещений.

2.Найти коэффициенты приведения длины и расчетные длины сжатых стержней.

3.Изобразить схему деформирования рамы при потере устойчивости.

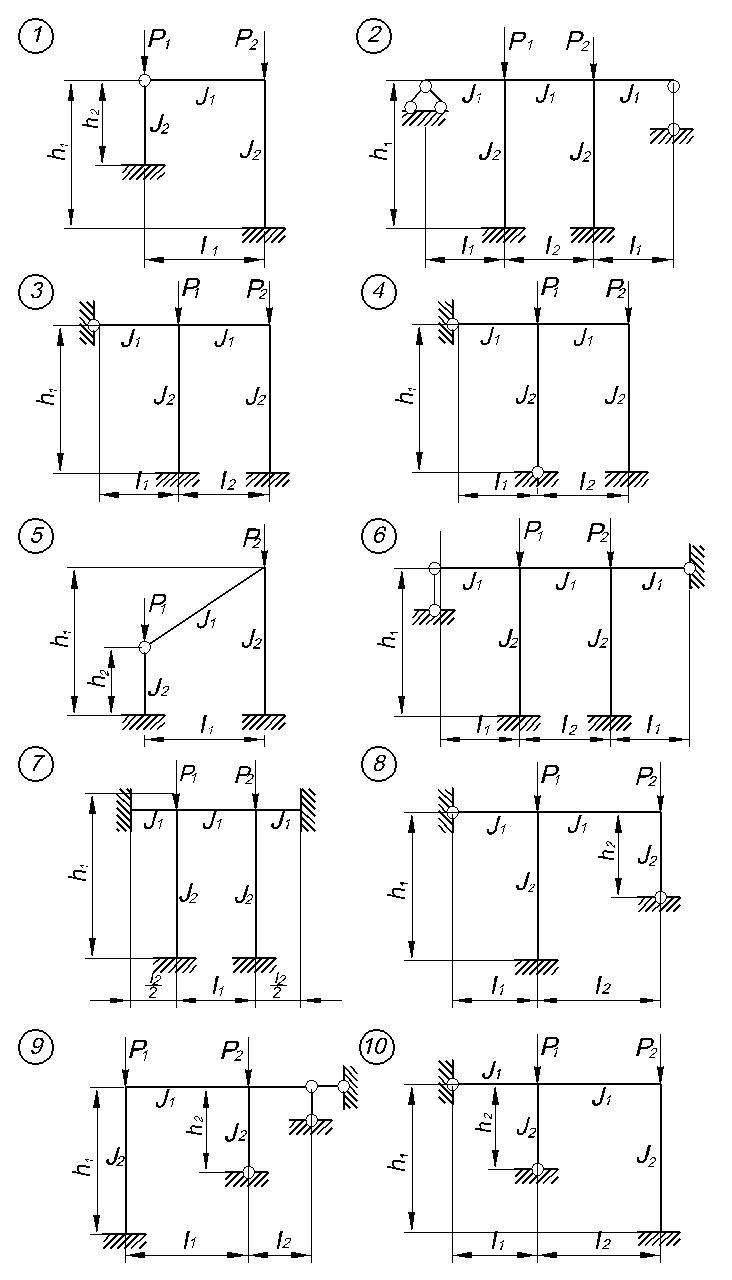
Рисунок 42

Таблица 4

Первая цифра шифра	l1 м	h1 м	Вторая цифра шифра	α=P1/P2	l2	Последняя цифра шифра (№ схемы)	h2 м	l1:l2
1	4	4	1	1,2	4	1	2	0,9
2	5	10	2	1,3	5	2	0	0,8
3	6	9	3	1,4	6	3	0	0,7
4	7	8	4	1,5	7	4	0	0,6
5	8	7	5	1,6	8	5	3	0,5
6	9	6	6	1,7	9	6	0	1,2
7	10	5	7	1,8	10	7	0	1,4
8	11	3	8	1,9	11	8	4	1,5
9	12	11	9	2,0	12	9	5	1,6
0	13	12	0	2,5	13	0	6	1,8

Методические указания

Решению задачи должно предшествовать изучение раздела устойчивости упругих систем [2], [8].

Все предлагаемые рамы целесообразно решать ме­тодом перемещений. Так как внешние нагрузки дейст­вуют вдоль оси сжатых стержней, то, очевидно, грузовых эпюр в основ­ной системе не будет и, следовательно, свободные члены канонических уравнений обратятся в нуль.

Построение единичных эпюр для сжатых стоек (от приложен­ных к узлам сил Р) следует проводить по специальным таблицам 5, а для ригелей — по обычным таблицам метода перемещений (3).

Специальные таблицы эпюр мо­ментов и необходимых функций для метода перемеще­ний лучше всего взять в пособии проф. А.Ф.Смирнова «Таблицы функций для расчета стержневых систем на устойчивость», таблица 2 (изд. МИИ. 1965 г.). Такие же таблицы можно найти в других источ­никах. Можно пользоваться более сокращенной таблицей 2, приложения 2 [2].

Коэффициенты канонических уравнений будут вклю­чать в себя некоторые функции и от параметров

где P_i и P_k – силы, действующие вдоль осей сжатых элементов h_i и; h_i; EJ_i и EJ_k

– жесткости стоек.

По заданию силы P_i и P_k связаны между собой коэффициентом α, поэтому параметры v и v_k окажутся связанными соотношением:

Для нахождения Р_Кр составляется и приравнивает­ся нулю определитель из коэффициентов канонических уравнений

Это уравнение решается подбором относительно v. Например, задавшись значением v_k, по зависимости между v_k и v_i определяют v_i. Затем из таблиц выписывают значения функций и , входящих в уравнение устойчивости. Если данные, значения φ не удовлетворяют уравнению, т. е. левая часть его не обращается в нуль, то нужно задаться другим значением и проделать все вычисления вторично и т. д. Когда будут найдены величины v_i и v_k, удовлетворяющие уравнению устойчивости, то по формулам

определяются значения критических сил.