5.Решение системы канонических уравнений (нахождение и ).

Опуская жесткость , система канонических уравнений имеет вид

Решая систему уравнений, получаем:

; .

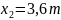6.По формуле: вычисляем значения изги-

бающих моментов и строим окончательную эпюру М.

;

; ;

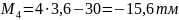Окончательная эпюра моментов М показана на рисунке 36

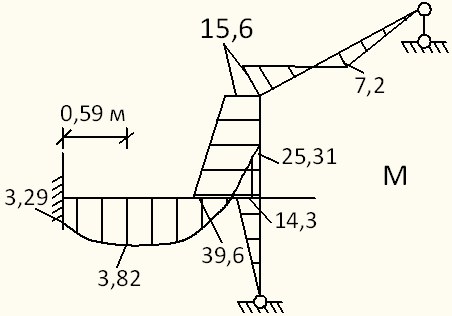
Рисунок 36

7. Проверки правильности построения эпюры м:

-статическая проверка. Рассматриваем равновесие узла 1.

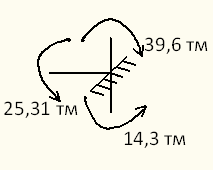
Узел находится в равновесии.

-деформационная проверка. Выбираем основную систему по методу сил (рисунок 37). На рисунке 38 представлена эпюра от действия силы

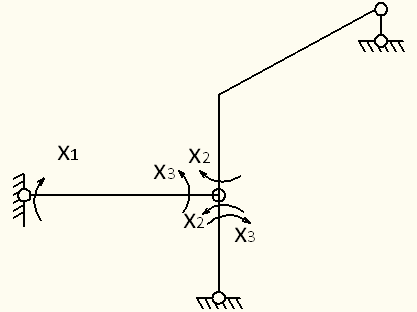
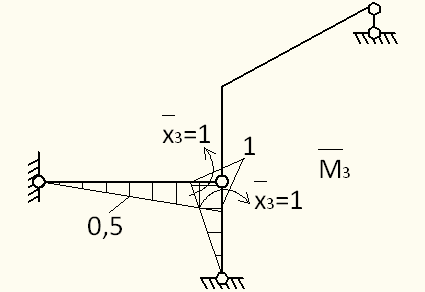
Рисунок 37 Рисунок 38

Вычисляем интеграл

.

7.Построение эпюры q и n.

Вычисляем значение Q на участках рамы.

; ;

;

;

; .

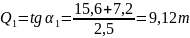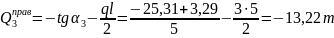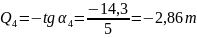Эпюра Q представлена на рисунке 39.

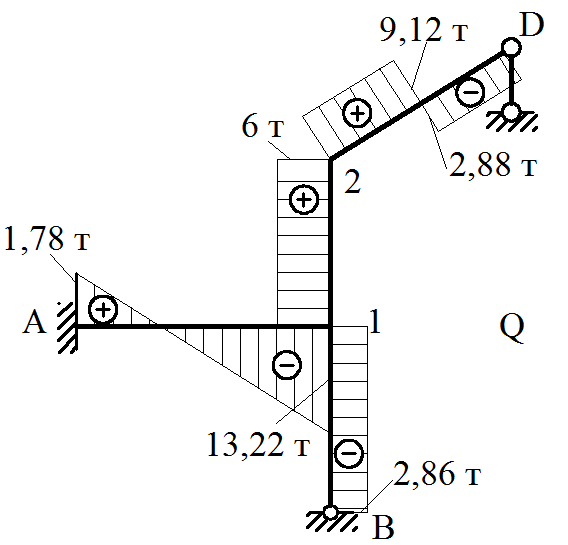
Рисунок 39

Находим сечение в раме с экстремальным изгибающим моментом.

Сечение на участке с равномерно распределенной нагрузкой, где Q=0, определяется следующим образом

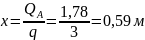
Максимальный изгибающий момент в этом сечении равен

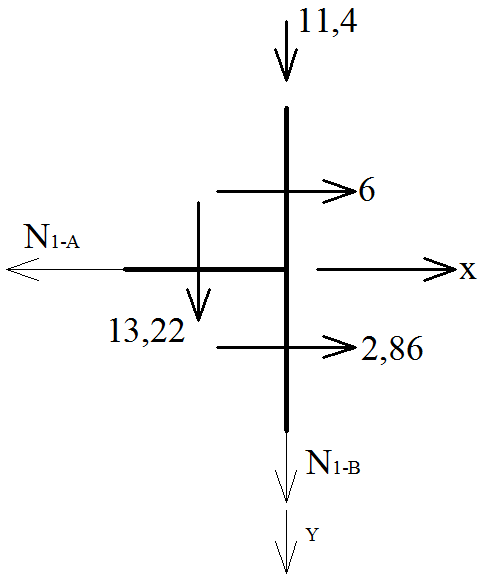
Значение продольной силы на участках определяем из равновесия вырезанного узла, рассматривая первоначально равновесие двухстержневого узла.

Узел 2.

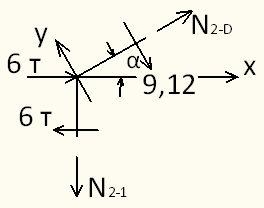
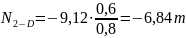
Узел 1

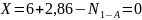
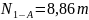
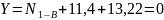
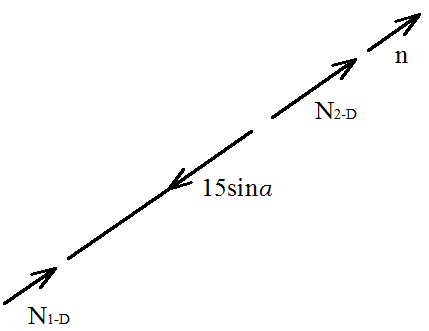Для определения продольной силы N_2-D рассмотрим равновесие стержня 2-D.

Эпюра продольных сил представлена на рисунке 40.

9.Проверка правильности построения эпюр M, Q, N.

Отделяем раму от опор. Вместо отброшенных связей в опорных сечениях прикладываем реакции, которые берем с эпюр M, Q, N. К выделенной части рамы прикладываем внешнюю нагрузку. Составляем уравнения равновесия рамы (рисунок 41):

;

;

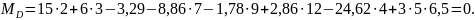
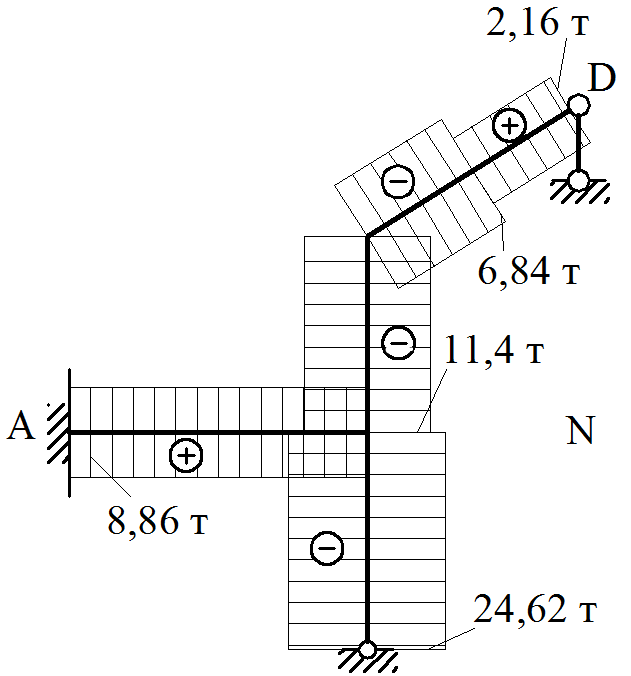
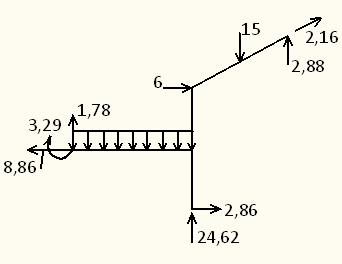
Рисунок 40 Рисунок 41

Глава 3. Расчет плоской рамы на устойчивость

Методические указания

Строительные конструкции, а также сооружение в целом, должны быть прочными, устойчивыми. Вопросы прочности и устойчивости простых сжатых стержней рассматри­вались в курсе сопротивления материалов. В строитель­ной механике изучаются более сложные случаи потери устойчивости стержней с любыми граничными усло­виями, стержней в упругосопротивляющейся среде, со­ставных и многопролетных стержней, а также устой­чивость рам, арок, пространственная устойчивость тон­костенных упругих стержней.

При изучении потери устойчивости инженерных сооружений необходимо хорошо представлять явление потери устойчивости, владение метода-ми, позволяющими определять значение критических нагрузок.

Основными методами расчета упругих систем на устойчивость приняты: динамический метод, как наиболее общий, применим для всех задач устойчивости; статический, приводящий к ре­шению дифференциальных уравнений изгиба или же к решению эквивалентных им однородных систем кано­нических уравнений метода сил или метода перемещений, и энергетический, при использовании которого не­обходимо задаваться уравнением изогнутой оси системы в момент потери устойчивости.

Изучение расчета рам на устойчивость следует огра­ничить случаем приложения критических сил к узлам, направление которых совпадает с осью сжатых стержней. Как и при расчете на прочность, задача решается методом сил или методом перемещений. Для указанного случая приложения на­грузки всегда удается выбрать такую основную систе­му, при которой канонические уравнения не будут со­держать свободных членов.

Определение коэффициентов канонических уравнений производится по специальным таблицам с учетом транс­цендентных коэффициентов, взятых по таблицам в за­висимости от параметра v

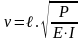₍₆₎

Таблицы трансцендентных функций метода сил и ме­тода перемещений можно найти в книгах [2], [8] (см. таблицу 6). Наиболее полные значения трансцендентных функ­ций можно получить в специальном пособии «Таблицы функций для расчета стержневых систем на устойчи­вость и колебания» (составлены проф. А. Ф. Смирновым и изданы МИИТ в 1965 г.).

Системы канонических уравнений при отсутствии сво­бодных членов имеют два решения:

а) все неизвестные равны нулю;

б)неизвестные отличны от нуля (что соответствует критическому состоянию), это возможно, когда опреде­литель из коэффициентов канонических уравнений равен нулю.

Раскрытие определителя дает уравнение устойчиво­сти, которое обычно решается подбором: нужно задать­ся такими величинами v, связанными между собой опре­деленным соотношением, чтобы соответствующие им зна­чения функций удовлетворяли уравнению устойчивости. По найденным значениям определяются величины кри­тических сил.

Для рам и арок часто приходится решать задачу по­тери устойчиво- сти второго рода, которая сводится к по­тере несущей способности, вслед-ствие развития больших перемещений при продольно-поперечном изгибе стержней.

Постановка задач устойчивости в матричной форме, предложенной А. Ф. Смирновым, больше всего подходит к решению на компьютерах.