Приведем задачу к виду озлп

F=-x₁+x₂+x₃ →max

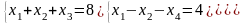
Умножим обе части неравенства (2) и (3) на «-1» и получим задачу

F=-x₁+x₂+x₃ →max

Построим симплекс-таблицу:

1-ая итерация

Выводим переменную х₅

Определим вводимую переменную – х_2,

Найден новый псевдоплан, его можно улучшить.

2-ая итерация

Выводим – х_4,

Вводим – х₁

3-ая итерация .

План Х_опт=(14/3; 2/3; 8/3; 0; 0) является оптимальным планом исходной задачи, т.к в колонке «План» нет отрицательных элементов и в индексной строке этого раздела нет отрицательных элементов. F_max= 32/3.

2.1.7. Постановка транспортной задачи

Общая постановка транспортной задачи заключается в определении оптимального плана перевозок некоторого однородного груза из «m» пунктов отправления (А₁, А₂, … , А_m) в «n» пунктов назначения (В₁, В₂, … , В_n). При этом в качестве критерия оптимальности обычно берется:

- минимальная стоимость перевозки всего груза;

- минимальное время доставки груза.

Рассмотрим транспортную задачу, критерием оптимальности которой является минимальная стоимость доставки груза.

Обозначим:

C_ij – тариф перевозки единицы груза из i-го пункта отправления в j-ый пункт назначения;

a_i – запасы груза в i-том пункте отправления;

b_j- потребности в грузе в j-ом пункте назначения;

x_ij – количество единиц груза, перевозимого из i-го пункта отправления в j-ый пункт назначения.

Тогда математическая постановка задачи состоит в определении минимального значения функции

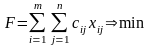( 1)

при условиях:

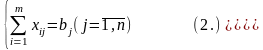
Обратные перевозки исключаются.

Планом транспортной задачи называется всякое неотрицательное решение системы линейных уравнений (2)и ( 3), определяемое матрицей X=[x_ij], где .

План X*=[x*_ij] , при котором функция (1) принимает свое минимальное значение, называется оптимальным планом транспортной задачи.

Обычно исходные данные транспортной задачи записываются в виде таблице:

Общее наличие груза у поставщиков равно единиц.

Общие потребности в грузе в пунктах назначения равно единиц.

Если 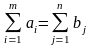(5),

то модель транспортной задачи называется закрытой.

Если условие (5) не выполняется, то модель транспортной задачи называется открытой. Для разрешимости транспортной задачи необходимо и достаточно, чтобы суммарные запасы в пунктах отправления были равны суммарным потребностям в пунктах назначения, т.е. задача была закрытого типа.

В случае превышения запасов над потребностями, т.е если , вводится фиктивный (n+1)-ый пункт назначения с потребностью, равной и нулевыми тарифами перевозок, c_i,n+1=0

Если 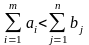,то вводится фиктивный (m+1)-ый пункт отправления с запасами и нулевыми тарифами перевозок, т.е c_j,m+1=0

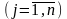
Число переменных x_ij в транспортной задаче с m пунктами отправления и n пунктами назначения равно m×n.

С учетом условий (2), (3) и (5) число линейно независимых уравнений равно m+n-1, следовательно, опорный план транспортной задачи содержит (может иметь) не более m+n-1 отличных от нуля компонентов.

Если в опорном плане число отличных от нуля компонентов в точности равно m+n-1 , то план является невырожденным, а если меньше, то вырожденным.

Транспортную задачу можно решать обычным симплекс-методом, однако учитывая громоздкость этого метода и специфику ограничений транспортной задачи (каждая переменная входит только в два уравнения системы, и коэффициенты при переменных равны 1), то для решения транспортной задачи разработаны свои методы.

Решение сводится к следующему:

1. Строится опорный план.

2. Проверяется опорный план на оптимальность.

3. Строятся улучшенные планы, которые также проверяются на оптимальность.

Процесс продолжается до тех пор, пока не будет найден оптимальный план транспортной задачи.