2.1.5. Двойственная задача линейного программирования

Каждой задаче линейного программирования можно определенным образом сопоставить некоторую другую задачу линейного программирования, называемую двойственной или сопряженной по отношению к исходной или прямой. Связь исходной и двойственной задач заключается в том, что решение одной из них может быть получено из решения другой.

Дадим определение двойственной задачи по отношению к общей задаче линейного программирования, состоящей в нахождении максимального значения функции

F = C₁X₁ + C₂X₂+…+C_nX_n (1)

при условиях

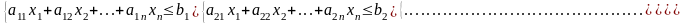(2)

x_j≥0 (j=1,n) (3)

Задача, состоящая в нахождении минимального значения функции

F*=b₁y₁+b₂y₂+…+b_my_m (4.)

при условиях

(5)

y_i≥0 (i=1,m) ( 6)

называется двойственной задачей по отношению к задаче (1) – (3)..

Задачи (1) – (3) и (4) – (6) образуют пару задач, называемую в линейном программировании двойственной парой.

Сравнивая две сформулированные задачи, видим, что двойственная задача по отношению к исходной составляется согласно следующим правилам:

1. Целевая функция исходной задача задается на max , а целевая функция двойственной задачи на min .

2. Матрица:

составленная из коэффициентов при неизвестных в система ограничений (2) исходной задачи и аналогичная матрица

в двойственной задаче получаются друг из друга транспонированием(т.е. заменой строк столбцами, а столбцов – строками).

3. Число переменных в двойственной задаче равно числу соотношений в системе ( 2) исходной задачи, а число ограничений в системе(5) двойственной задачи равно числу переменных в исходной задаче.

4. Коэффициентами при неизвестных целевой функции двойственной задачи являются свободные члены системы (2) исходной задачи, а правыми частями в системе ограничений двойственной задачи – коэффициенты при неизвестных в целевой функции исходной задачи .

5. Если переменная x_j исходной задачи может принимать лишь положительные значения, то j-тое условие в системе (5) двойственной задачи является неравенством вида «≥». Если же переменная x_j может принимать как положительные так и отрицательные значения, то j-тое соотношение в системе (5) является уравнением.

6. Если i-е соотношение в системе (2) исходной задачи является неравенством, то i-тая переменная двойственной задачи y_i≥0 . В противном случае переменная y_i может принимать как положительные так и отрицательные значения.

Двойственные пары задач обычно подразделяются на симметричные и несимметричные.

В симметричной паре двойственной задачи ограничения вида (2) исходной задачи и соотношения (5) двойственной задачи являются неравенствами вида « ≤», т.е переменные обеих задач могут принимать только неотрицательные значения.

2.1.6. Двойственный симплекс-метод

Он требует, чтобы задача была задана в виде основной задачи линейного программирования. Вместе с тем его можно применять при решении задач линейного программирования, у которых свободные члены системы ограничений могут быть любыми числами(как положительные , так и отрицательные).

Пусть требуется определить max значения функции:

F=C₁X₁+C₂X₂+…+C_nX_n →max

при условиях :

x₁p₁+x₂p₂+…+x_mp_m+x_m+1p_m+1+…+x_np_n= p_{o ,}

где:

x_j≥0 (j=1,n)

Таким образом, векторы р₁;p₂; … ;p_m – единичные векторы, образующие базис.

Среди чисел b_i имеются отрицательные (i=1,m).

В данном случае решение X = (b₁, b₂ , … ,b_m, 0, 0, … ,0) является решением системы линейных уравнений, представляющих решение исходной задачи, но не является решением самой исходной задачи.

Такое решение Х называют псевдопланом (т.к. по условию x_j≥0, а среди b_i есть отрицательные числа.)

Рассмотрим алгоритм двойственного симплекс-метода:

1. Составляют симплекс-таблицу и находят псевдоплан задачи.

2. Проверяют псевдоплан на оптимальность или устанавливают неразрешимость задачи. Если в колонке «План» нет отрицательных чисел, то псевдо план является оптимальным. Если отрицательные числа имеются, то переходят к новому псевдоплану, либо устанавливают неразрешимость задачи.

3. Выбирают направляющую строку путем определения наибольшего по модулю отрицательного числа в колонке «План». Затем определяют направляющий столбец с помощью нахождения наименьшего по абсолютной величине отношения элементов «m+1»-ой строки к соответствующим отрицательным элементам направляющей строки.

В результате определяют вектор, выводимый из базиса и вектор, вводимый в базис.

4. Находят новый псевдоплан путем пересчета элементов нового раздела симплекс-таблицы и повторяют все действия с пункта 2.

Пример: найти максимальное значение функции

F=-x₁+x₂+x₃ →max

при условиях: