Раздел 2. Детерминированные задачи

Тема 2.1. Линейное программирование

2.1.1. Модели линейного программирования

Составной частью математического программирования является линейное программирование. Впервые постановка задачи линейного программирования, в виде предложения по составлению оптимального плана перевозок, позволяющего минимизировать суммарный километраж, дана в работе советского ученого экономиста А.Н.Толстого в 1930 году.

Систематическое исследование задач линейного программирования и разработка общих методов их решения начата в работах советского ученого Л.В. Канторович (1939 г.), который предложил общий метод решения этих задач. Он же совместно с М.К.Гавуриным разработал метод потенциалов, который применяется при решении транспортных задач (1949 г.)

Методам линейного программирования посвящено много работ зарубежных, и прежде всего американских ученых.

Основной метод решения задач линейного программирования (симплекс метод) был опубликован в 1949 году Данцигом.

В настоящее время методы линейного программирования развиваются главным образом в направлении выявления конкретных экономических задач, к решению которых оно может быть применено, а также по пути создания более удобных алгоритмов для решения задач на ЭВМ.

Линейное программирование – это наука о методах исследования и отыскания наибольших и наименьших значений линейной функции, на неизвестные которой наложены линейные ограничения

Если система ограничений задачи линейного программирования включает неравенство и уравнение, то задача называется общей задачей линейного программирования, а если только уравнение – то основной задачи линейного программирования (ОЗЛП).

Основная задача линейного программирования заключается в следующем:

Найти неотрицательное значение переменных х₁, х₂, … , х_n , удовлетворяющих “m” условиям - равенства:

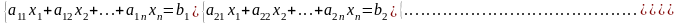
и обращающих в max(min) целевую функцию:

F=C₁X₁+C₂X₂+…+C_nX_n→max (min)

x_j≥0 ( )

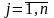Если отыскивается мах функции, то задача линейного программирования называется задачей максимизации, а если min , то задачей минимизации

Задача минимизации легко сводится к задачи максимизации путем замены знаков коэффициентов целевой функции на противоположные.

Допустимым решением основной задачи линейного программирования называют всякую совокупность неотрицательных значений х₁, х₂, x_n , удовлетворяющих системе ограничений.

Оптимальным называют то из допустимых решений, которое обращает в max(min) целевую функцию.

Всякая общая задача линейного программирования может быть сведена к равносильной ей основной задаче путем введения новых неизвестных, называемых дополнительными неизвестные. Переменные, которые входят в ограничения исходной задачи, называется основными

В неравенствах типа «<=» к левым частям неравенств прибавляются дополнительные переменные, а в неравенствах типа «>=» из левых частей неравенств вычитаются дополнительные переменные.

Число дополнительных переменных равно числу ограничений - неравенств.

В целевую функцию все дополнительные переменные входят с нулевыми коэффициентами.