3. Классификация математических моделей

При построении математических моделей исходными являются только те свойства объекта , которые могут быть описаны количественно, и только те связи между свойствами, которые поддаются описанию языком математики.

Математические модели классифицируются по нескольким признакам:

1. По использованному при построении модели математическому аппарату

различают:

а) аналитические модели, когда явления описываются с помощью алгебраических уравнений и неравенств, а если требуется рассмотреть явление в динамике, то применяются дифференциальные уравнения (обыкновенные и в частных производных). Эти модели более грубые, учитывают меньшее число факторов, всегда требуют каких -то допущений и упрощений, но результаты расчета по ним легче обозримы, более четко выделены закономерности , и они лучше приспособлены для поиска оптимальных решений;

б) модели, использующие метод статистического моделирования, когда развитие операции и ее исход зависят от большого числа взаимосвязанных случайных факторов. Эти модели, по сравнению с аналитическими, более точны и подробны, учитывают больше факторов, но они громоздки, хуже обозримы, требуют большего расхода времени на решение, в них затруднен поиск оптимального решения;

в) имитационные модели, отражающие такие процессы, в ход которых может время от времени вмешиваться человек. Эти модели известны под названием «деловые игры».

2. П о характеру неопределенности цели операции модели бывают:

а) детерминированные (жесткие) - строятся в том случае, когда все условия операции известны заранее , то есть не содержат неопределенности. Обычно эти модели описываются системами уравнений;

б) стохастические - строятся в том случае, когда параметры операции подвержены воздействию случайных не контролируемых факторов. В этих моделях используются методы теории вероятности и математической стати

3. По числу критериев, характеризующих операцию, различают:

- модели, содержащие одну целевую функцию (однокритериальные);

- многокритериальные модели, когда эффективность операции характеризуется несколькими целевыми функциями.

4. С учетом фактора времени модели бывают:

- статические , если параметры модели не изменяются во времени;

- динамические, если хотя бы один параметр изменяется во времени.

4. Построение простейших математических моделей

При построение математических моделей необходимо:

- определить элементы решения;

- определить , что является критерием эффективности задачи, то есть целевой функцией;

- составить систему ограничений с учетом дисциплинирующих факторов задачи.

Рассмотрим пример построения простейшей математической модели: задачи о планировании производства.

Предприятие производит изделия трех видов: U₁,U₂,U₃. По каждому виду изделий известен план: b₁,b₂,b₃. План может быть перевыполнен, но в определенных границах: не более p₁,p₂,p₃ единиц соответственно .

На изготовление изделий идет какое-то сырье. Всего имеется 4 вида сырья: S₁,S₂,S₃,S₄, причем, запасы сырья ограничены числами y₁,y₂,y₃,y₄ соответственно. Для изготовления единицы изделия i-го вида (i=1,3) требуется A[i,j] единиц сырья j-го вида (j=1,4). При реализации единицы изделия i-го вида получают прибыль С_i.

Требуется так спланировать производство, чтобы план был выполнен или перевыполнен, но при отсутствии затоваривания, а суммарная прибыль обращалась бы в максимум.

Решение

Для удобства условие задачи запишем в таблицу

Изделие	Сырьё				План выпуска	Условие спроса	Прибыль с реализацией
	S1	S2	S3	S4
U1	A11	A12	A13	A14	B1	β1	C1
U2	A21	A22	A23	A24	B2	β2	C2
U3	A31	A32	A33	A34	B3	β3	C3
Запасы сырья	γ1	γ2	γ3	γ4

1. Определим, что будет являться элементами решения.

В нашем примере это будет количество выпускаемых изделий каждого типа

Обозначим их через х₁, х₂, х₃ соответственно.

2. Целевой функцией будет максимальная прибыль от реализации. Запишем ее в виде уравнения:

F=C₁X₁+C₂X₂+C₃X₃→max (1)

или

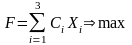
3. Составим ограничения (дисциплинирующие условия)

а) с учетом выполнения плана

(2)

б) с учетом условия спроса

(3)

в) с учетом запасов сырья и нормы расходов.

(4)

Целевая функция (1) с ограничениями (2 )- (4) и представляют математическую модель задачи.