
- •Финансово-технологическая академия Колледж космического машиностроения и технологий
- •Дисциплина Математические методы
- •Раздел1. Основы моделирования ………………………………………………… .3
- •Раздел 2. Детерминированные задачи……………………………………………..7
- •Тема 2.1. Линейное программирование…………………………………………7
- •Основные понятия исследования операций
- •Рассмотрим основные понятия теории исследования операций.
- •Модели, их классификация, особенности
- •Классификация математических моделей
- •По использованному при построении модели математическому аппарату
- •Построение простейших математических моделей
- •Раздел 2. Детерминированные задачи
- •Тема 2.1. Линейное программирование
- •2.1.1. Модели линейного программирования
- •2.1.2. Графический метод решения задач линейного программирования
- •2.1.3. Симплекс-метод для решения задач линейного программирования
- •2.1.4. Симплекс-метод c искусственным базисом
- •2.1.5. Двойственная задача линейного программирования
- •2.1.6. Двойственный симплекс-метод
- •Приведем задачу к виду озлп
- •2.1.7. Постановка транспортной задачи
- •2.1.8. Построение опорного плана транспортной задачи
- •2.1.9. Определение оптимального плана транспортной задачи
- •Тема 2.2. Нелинейное программирование
- •Тема 2.3. Алгоритмы на графах
- •2.3.1. Основные сведения из теории графов
- •Пути и маршруты в графе
- •Вес и длина пути
- •Степени вершин
- •2.3.2. Матричное представление графа
- •Поиск кратчайшего пути в графе
- •Первая итерация
- •Вторая итерация
- •Третья итерация
- •Четвёртая итерация
- •Поиск максимального потока в графе
- •Задача о максимальном потоке
- •Тема 2.4. Динамическое программирование
- •2.4.1. Постановка задачи динамического программирования
- •2.4.2. Моделирование многошаговых процессов
- •2.4.3. Принцип оптимальности
- •Раздел 3. Задачи в условиях неопределенности системы массового обслуживания
- •Характеристики входа
- •Поведение клиентов
- •Характеристики очереди
- •Характеристики процесса обслуживания
- •Параметры моделей очередей
Параметры моделей очередей
При анализе систем массового обслуживания наиболее часто используются следующие технические и экономические характеристики:
среднее время, которое клиент проводит в очереди;
средняя длина очереди;
среднее время, которое клиент проводит в системе обслуживания (время ожидания плюс время обслуживания)
среднее число клиентов в системе обслуживания;
вероятность того, что система обслуживания окажется незанятой;
вероятность определенного числа клиентов в системе. Среди экономических характеристик наибольший интерес
представляют:
издержки ожидания в очереди;
издержки ожидания в системе;
издержки обслуживания.
В зависимости от сочетания приведенных выше характеристик, могут рассматриваться различные модели систем массового обслуживания. Здесь мы познакомимся с несколькими наиболее известными моделями. Все они имеют следующие общие характеристики: • пуассоновское распределение вероятностей поступления заявок;
стандартное поведение заявок;
правило обслуживания FIFO;
единственная фаза обслуживания.
Модели систем массового обслуживания
Модель А.
Модель одноканальной системы массового обслуживания с пуассоновским входным потоком заявок и экспоненциальным временем обслуживания.
Наиболее часто встречаются задачи массового обслуживания с единственным каналом. В этом случае клиенты формируют единственную очередь, которая обслуживается одним сотрудником.
Предположим, что для систем этого типа выполняются следующие условия:
заявки обрабатываются по принципу «первым пришел — первым обслужен», причем каждый клиент ожидает своей очереди до тех пор пока не будет обслужен, независимо от длины очереди;
появление заявки является независимым событием, однако, среднее число заявок, поступающих в единицу времени, неизменно;
процесс поступления заявок описывается пуассоновским распределением, причем заявки поступают из неограниченного множества;
время обслуживания описывается экспоненциальным распределением вероятностей;
темп обслуживания выше темпа поступления заявок. Если эти условия выполняются, то модель А описывается
следующими уравнениями: М/М/1 — простая система;
λ — число заявок в единицу времени;
m — число клиентов, обслуживаемых в единицу времени;
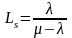 —
среднее число клиентов в системе;
—
среднее число клиентов в системе;
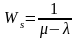 —
среднее время обслуживания одного
клиента в системе (включает время
ожидания и время обслуживания);
—
среднее время обслуживания одного
клиента в системе (включает время
ожидания и время обслуживания);
 − среднее число клиентов в очереди;
− среднее число клиентов в очереди;
ЛИТЕРАТУРА
Акулич И.Л. Математическое программирование в примерах и задачах. М., Высшая школа, 1986.
Афанасьев М.Ю., Багриновский К.А., Матюшок В.М. Прикладные задачи исследования операций. М., Инфра-М, 2006.
Вентцель Е.С. Исследование операций. М., Советское радио, 1972.
Кристофидес
Кузнецов Ю.Н., Кузубов В.И., Волощенко А.Б. Математическое программирование. М., Высшая школа/ 1980.
Нит И.В. Линейное программирование. М., Изд. МГУ, 1978.
