Вес и длина пути

Иногда дугам графа G приписываются числа- дуге (x_i x_j) ставится в соответствие некоторое число C_ij , называемое весом или длиной дуги.

В этом случае граф G называется графом со взвешенными дугами.

Если веса (числа v_j) приписываются вершинам x_j, то такой граф называется графом со взвешенными вершинами, а сами числа v_j – весами вершин.

Если в графе веса приписаны и дугам и вершинам, то такой граф называется просто взвешенным.

При рассмотрении пути μ , представленного последовательностью дуг а₁ , а₂ , …. , а_q за его вес принимается число l(μ), равное сумме весов всех дуг, входящих в этот путь, причем каждая дуга считается столько раз, сколько она встречается в данном пути.

Длиной пути μ называется количество дуг, входящих в него, причем каждая дуга считается столько раз, сколько она входит в этот путь.

Степени вершин

Число дуг, которые имеют вершину x_i своей начальной вершиной, называется полустепенью исхода вершины x_i. Обозначается d_о(x_i).

Число дуг, которые имеют вершину x_i своей конечной вершиной, называется полустепенью захода вершины x_i. Обозначается d_t(x_i).

Например: для графа, изображенного на рисунке, имеем:

d_о(x₁)=2 d_t(x₁)=2

d_о(x₂)=2 d_t(x₂)=2

d_о(x₃)=0 d_t(x₃)=2

d_о(x₄)=1 d_t(x₄)=1

d_о(x₅)=2 d_t(x₅)=2

d_о(x₆)=3 d_t(x₆)=1

Для любого графа G

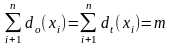
где n – количество вершин в графе;

m – количество дуг в графе.

2.3.2. Матричное представление графа

Для задания структуры графа удобно использовать матрицы следующих видов:

1. Матрицу смежности

Она квадратная, n-го порядка, обозначается A=[a_ij]

Элементы матрицы определяются из условия:

- a_ij = 1, если в графе есть дуга (x_i x_j)

- a_{i j}= 0, если в графе нет дуги (x_i x_j).

Например, для графа, изображенного на рисунке,

имеем следующую матрицу смежности

Эта матрица полностью определяет структуру графа:

Сумма всех элементов строки x_{i i} дает полустепень исхода вершины x_i. Сумма элементов столбца x_i дает полустепень захода вершины x_i.

Множество столбцов, имеющих единицы в строках x_i, соответствует множеству Г(x_i).

Множество строк, которые имеют единицы в столбце x_i ,соответствует множеству Г^-1(x_i)

2. Матрицу инциденций.

Эта матрица размерностью n×m , обозначается B=[b_ij].

Элементы матрицы определяются следующим образом:

- b_ij= 1, если x_i - начальная вершина дуги a_j;

- b_ij=-1, если x_i - конечная вершина дуги a_j;

- b_ij= 0, если x_i не является концевой вершиной дуги a_j или дуга a_j является петлей.

Например, для графа, изображенного на рисунке,

Имеем следующую матрицу инциденций:

Если граф неориентированный, то его матрица инциденции определяется так же как и для ориентированного графа, за исключением того , что все элементы равные «-1» заменяются на «+1»

3. Поиск кратчайшего пути в графе

Поиск кратчайшего пути в графе между двумя точками - это нахождение такой последовательности дуг (или дуги), ведущей от начальной точки до конечной, при которой сумма их весов будет минимальной.

Рассмотрим задачу поиска кратчайшего пути между двумя заданными вершинами S и t для случая неотрицательной матрицы весов.

Наиболее эффективный алгоритм решения такой задачи создал Дейкстра. Этот метод основан на приписывании вершинам временных пометок, причем, пометка вершины дает верхнюю границу длины пути от S к этой вершине. Эти пометки (их величины) постепенно уменьшаются с помощью итерации, и на каждом шаге итерации только одна из временных пометок становится постоянной. Это означает, что эта пометка дает точную длину кратчайшего пути от S к рассматриваемой вершине

Рассмотрим суть алгоритма Дейкстры.

Пусть l(X_i) - пометка вершины X_i.

Присваивание начальных значений

Шаг первый

Положить 1(S) = 0 и считать эту пометку постоянной.

Положить l(X_i) = ∞ для всех X_i ≠ S , и считать эти пометки временными.

Положить р = S,

где р- вспомогательная величина, равная номеру той вершины, которая на данном шаге получает постоянную пометку.

Обновление пометок

Шаг второй

Для Х є Г(р), пометки которых временные, изменить их в соответствии со следующим выражением:

l(X_i)=min[ l(X_i) ; l(p)+c(p,X_i) ] (1)

Превращение пометки в постоянную

Шаг третий

Среди всех вершин с временными пометками найти такую, для которой l(X_i*)=min[l(X_i)]

Шаг четвертый

Считать пометку вершины X_i* постоянной и положить p =X_i*.

Шаг пятый

а) Если надо найти путь от S к t:

• если p = t, то 1(р) является длиной кратчайшего пути, конец задачи;

• если р ≠ t, то перейти ко второму шагу.

б) Если требуется найти путь от S ко всем остальным вершинам:

• если все вершины отмечены как постоянные, то пометки этих вершин дают длины кратчайших путей, конец задачи;

• если некоторые пометки являются временными, перейти ко второму шагу.

Длина кратчайшего пути от исходной вершины S к любой вершине графа t равна величине постоянной пометки этой вершины t, т.е. l(S,t)=l(t).

Для нахождения самого пути воспользуемся соотношением:

l(X_i*)+c(X_i*,X_i)=l(X_i), (2)

где X_i* - вершина, непосредственно предшествующая вершине X_i в кратчайшем пути от S к t

Если условие (2) выполняется, то дуга (X_i*,X_i) входит в кратчайший путь.

Используя изложенный выше алгоритм, определим кратчайший путь в графе G от заданной вершины Х₅ ко всем вершинам.

Шаг1 Присвоим начальные пометки вершинам:

l(X₅) = 0⁺ ;

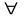X_i ≠ X₅ , l(X_i) = ∞;

p = X₅ ,