Тема 2.3. Алгоритмы на графах

2.3.1. Основные сведения из теории графов

Часто бывает полезно и наглядно изображать некоторую ситуацию в виде рисунка, состоящего из точек(вершин), представляющих основные элементы ситуации, и линий (ребер), соединяющих определенные пары этих вершин и представляющих связи между ними. Такие рисунки известны под общим названием графов.

Графы встречаются во многих областях под разными названиями:

- «структуры» в гражданском строительстве;

- «сети» в электротехнике;

- «социограммы» в социологии и экономике;

- «молекулярные структуры» в химии;

- электрические или газовые «распределительные сети» и т.д.

Благодаря своему широкому применению теория графов в последние годы интенсивно развивается. В большей мере этому способствует также прогресс в области развития вычислительной техники.

Таким образом, граф G задается множеством вершин х₁, х₂, … , x_n (которое обозначается через Х) и множеством линий - ребер а₁, а₂, …, a_m (которое обозначается символом А), соединяющих между собой все или часть вершин.

Принято обозначать граф в виде G=(X,A).

Если ребра графа ориентированы, что обычно показывается стрелкой, то они называются дугами, и граф в этом случае называется ориентированным.

Если ребра не имеют ориентацию, то граф называется неориентированным.

Граф, содержащий дуги и ребра, называется смешанным.

Если граф G=(X,A)является ориентированным, но мы хотим пренебречь направленностью дуг, то неориентированный граф, соответствующий первоначальному заданному, обозначают 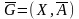и называют неориентированным дубликатом (неориентированным двойником) графа G.

Каждая дуга графа соединяет пару вершин - начальную и конечную, следовательно, любую дугу можно обозначить упорядоченной парой вершин.

Например: для графа, изображенного на рисунке имеем:

а₁=(х₁ х₂)

а₂=(х₂ х₅)

а₃=(х₁ х₃)

а₄=(х₃ х₄)

а₅=(х₃ х₅) и (х₅ х₃) или 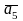=(х₃ х₅)

а₆=(х₄ х₅)

а₇=(х₂ х₃)

Ориентированный граф можно задать множеством вершин и соответствий «Г» (гамма).

Соответствие Г(x_i) представляет собой множество вершин x_j ∈ X, для которых в графе G существует дуга (x_i , x_j )

Тогда для графа, изображенного на рисунке, имеем:

Г(х₁)={х₂ , х₃}

Г(х₂)={х₃ , х₅}

Г(х₃)={х₂ , х₃}

Г(х₄)={х₂}

Г(х₅)={ х₃}

Таким образом, для неориентированного графа или смешанного графа при составлении соответствия ребро заменяется двумя противоположно направленными дугами, соединяющими те же вершины.

Граф G в этом случае задается парой G=(Х,Г)

Обратное соответствие Г^-1(x_i) представляет собой множество вершин х_j принадлежащих множеству х для которых в графе G существует дуга (x_j , x_i), т.е вершина X_i является конечной в рассматриваемых дугах.

Тогда для графа , изображенного на рисунке имеем:

Г^-1(x₁)- пустое множество

Г^-1(x₂)= {х₁}

Г^-1(x₃)= {х₁ , х₂ , х₅}

Г^-1(x₄)= {х₃}

Г^-1(x₅)= {х₂ , х₃ , х₄ }

Пути и маршруты в графе

Путем ориентированного графа G называется последовательность дуг, в которой конечная вершина всякой дуги, отличной от последней, является начальной вершиной следующей дуги.

Путь можно задавать последовательностью дуг или последовательностью вершин.

Например, для графа изображенного на рисунке, имеем:

μ₁= а₁ , а₇ , а₄

μ₂= а₃ , а₄

или

μ₁= х₁ , х₂ , х₃ , х₄

μ₂= х₁ , х₃ , х₄

Маршрутом называется последовательность ребер а₁, а₂, … , а_q , в которой каждое ребро а_i , за исключением возможно первого и последнего ребра, связано с ребрами a_i-1 и а_i+1 своими концевыми вершинами.

Если в пути или в маршруте начальная и конечная вершина совпадают, то такой путь называется циклом или циклическим контуром.

Петлей называется дуга, начальная и конечная вершины которой совпадают (например a₄ , a₅).