2.3 Экономико – математическое моделирование

Проведем исследование влияния факторов на изменение суммы затрат на ремонт основных средств.

Имеются следующие данные о зависимости суммы затрат на ремонт основных средств y (тыс. руб.) от объёма выпущенной продукции – x₁ (тыс. руб.) и среднегодовой стоимости основных средств – x₂ (тыс. руб.).

Таблица 5

Исходные данные

Показатели	Годы
	2003	2004	2005	2006	2007	2008	2009
х1 (Объем продукции, тыс.руб.)	134550	183250	241000	302500	365613	518089	474615
х2 (Среднегодовая стоимость основных средств, тыс. руб.)	103210	103050	102989	102862	102754	102573	102357
у (затраты на ремонт всего, тыс. руб.)	14000	16234	18120	20356	22008	23197	25710

Построим регрессионную модель и проведем серию необходимых проверок для подтверждения её статистической значимости.

По данным таблицы построим область рассеяния.

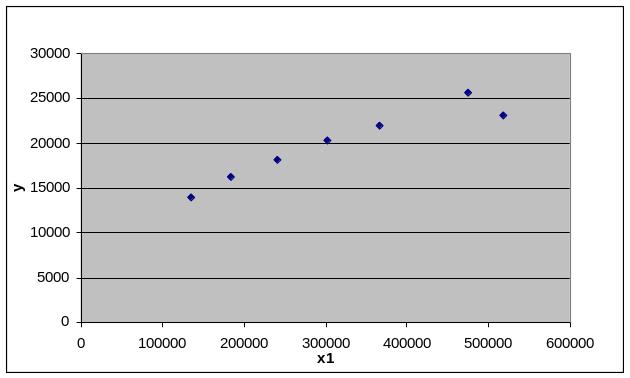
Рис.4. Влияние объема выпущенной продукции на затраты на ремонт основных фондов

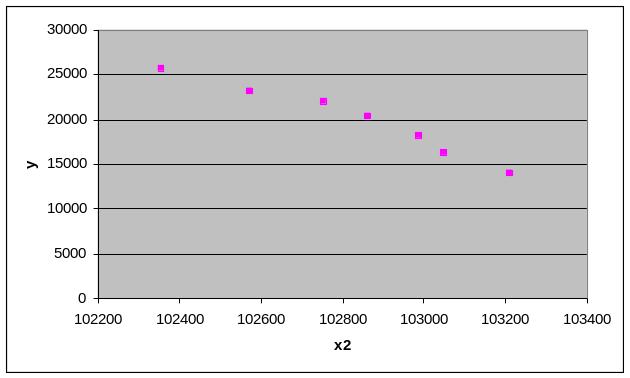
Рис.5. Влияние среднегодовой стоимости основных средств на затраты на ремонт основных фондов

Для того, чтобы выбрать фактор, наиболее тесно связанный с зависимой переменной, оценим величину влияния факторов при помощи коэффициента корреляции. Расчёт коэффициента корреляции проведем с помощью программного средства Excel. Результат корреляционного анализа представлен в таблице 6.

Таблица 6

Результат корреляционного анализа

	y	x1	x2
y	1
x1	0,952561659	1
x2	-0,982466501	-0,951844581	1

Анализ матрицы коэффициентов парной корреляции показывает, что зависимая переменная y имеет тесную связь с х₁ и х₂, так как коэффициенты корреляции по абсолютной величине больше 0,7.

Построим регрессионную модель:

y = &₀ + &₁x₁ + &₂x₂, (1)

где

у – затраты на ремонт основных фондов (тыс. руб.);

х₁ – объёмы выпуска продукции (тыс. руб.);

х₂ – среднегодовые стоимости основных средств (тыс. руб.).

Определим коэффициенты &₀, &₁, &₂, используя данные, приведенные в таблице 7.

Таблица 7

Признак	Среднее значение	Среднее квадратичес-кое отклонение ( )	Линейный коэффициент парной корреляции
у (затраты на ремонт всего, тыс. руб.)	19946	3792,5	–
х1 (Объем продукции, тыс.руб.)	317088,1429	133526,7542	ryx1= 0.952561659
х2 (Среднегодовая стоимость основных средств, тыс. руб.)	102827,8571	271,142255	ryx2=– 0.982466501 rx1x2=– 0.951844581

Для расчёта применим метод стандартизации переменных и построим искомое уравнение в стандартизированном масштабе:

Расчёт ß-коэффициентов выполним по формулам:

= 0,18518878

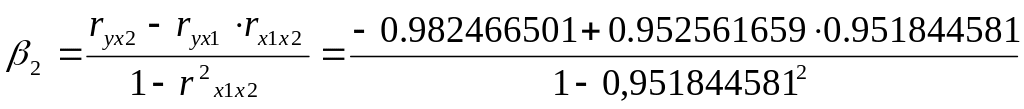= – 0,80619557

Получим уравнение:

Для построения уравнения в естественной форме рассчитаем &₁ и &₂, используя формулы для перехода от ß_i к &_i:

=0.005259833

= – 11.276356388

Значение &₀ определим из соотношения

&₀ =

&₀ = 19946 – 0,005259833 ∙ 317088,1429 + 11,276356388 ∙ 102827,8571 =

= 1177801,7326

В результате проведенных расчётов получаем уравнение множественной регрессии:

у = 1177801,733 + 0,005 ∙ х₁ – 11,276 ∙ х₂

Результаты регрессионного анализа содержатся в таблице 8.

Таблица 8

Результаты регрессионного анализа

Y-пересечение	1177801,733
Переменная Х1	0,005
Переменная Х2	– 11,276

Следовательно, уравнение регрессии зависимости затрат на ремонт основных фондов имеет вид:

у = 1177801,733 + 0,005 ∙ х₁ – 11,276 ∙ х₂

Параметры уравнения регрессии показывают, что:

– при увеличении фактора Х₁ – объема выпуска продукции – на 1 тыс. руб., величина затрат на ремонт увеличится в среднем на 0,005 тыс.руб. (или на 5 руб.). Это происходит в связи с тем, что увеличение выпуска продукции потребует дополнительной нагрузки на оборудование и прочие основные фонды и потребует дополнительных расходов на ремонт;

– при уменьшении среднегодовой стоимости основных средств на 1 тыс. руб., затраты на их ремонт уменьшатся на 11,276 тыс. руб. Это объясняется тем, что сокращение количества работающего оборудования и других основных фондов уменьшит необходимость в ремонте.

Вычислим значения R², R, R_ср² для регрессии. Расчет линейного коэффициента множественной корреляции выполним по формуле:

0,9841

Нормированный R-квадрат:

n – число наблюдений;

k – число факторов.

= 0,9528

Полученные данные занесем в таблицу 9.

Таблица 9

Регрессионная статистика

Множественный R	0,9841
R-квадрат	0,9685
Нормированный R-квадрат	0,9528
Наблюдения	7

Так как множественный R=0,9841 больше 0,7, то связь между факторами х₁, х₂ и у – тесная.

Значение коэффициента детерминации R²=0,9685 показывает долю вариации результативного признака под воздействием изучаемых факторов. Следовательно, около 97% суммы затрат на ремонт зависят от включенных в модель факторов (среднегодовой стоимости основных средств и объёма продукции), а 3% зависят от факторов, не включенных в модель.

Нормированный R-квадрат свидетельствует, что при добавлении ещё одного фактора в модель, её обхват составит 95%. Таким образом, выбрано оптимальное число факторных признаков.

Проведем тест, который проверяет совместную способность k независимых переменных объяснить зависимую переменную.

Этот тест является проверкой нулевой гипотезы: . Нулевая гипотеза проверяется с помощью F-критерия:

=61,4921

С помощью F-статистики проверяется, действительно ли объясненная сумма квадратов отклонений превышает ту сумму квадратов отклонений, которая может быть случайной. Критический предел для F-статистики находится как значение F-распределения с параметрами (уровень значимости), k (число степеней свободы числителя), n–k–1 (число степеней свободы знаменателя).

Зададимся критерием значимости =0,05 и по статистической таблице найдём F_табл=6,94.

F=61,4921 6,94, т.е. гипотеза Н₀ о случайной природе оцениваемых характеристик отклоняется и признается их статистическая значимость и надежность.

Проведем ещё одну проверку на определение серийной корреляции ошибок. Воспользуемся критерием Дарбина – Уотсона. Выберем уровень значимости 5 %.

Таблица 10

Расчёт критерия Дарбина – Уотсона

у	ei	ei–1	ei–ei–1	(ei–ei–1)2	ei2
14000	-678,523	0	-678,523	460393,4615	460393,4615
16234	-492,183	-678,523	186,34	34722,5956	242244,1055
18120	417,231	-492,183	909,414	827033,8234	174081,7074
20356	913,679	417,231	496,448	246460,6167	834809,315
22008	1032,306	913,679	118,627	14072,36513	1065655,678
23197	-582,03	1032,306	-1614,34	2606080,721	338758,9209
25710	-287,276	-582,03	294,754	86879,92052	82527,50018
139625	323,204	610,48	-287,276	4275643,504	3198470,688

Вычислим статистику Дарбина-Уотсона по формуле:

=1,3368

и проверим выполнение следующих гипотез:

Н₀: автокорреляции не существует;

Н₁: существует положительная автокорреляция.

d_L=0,47; d_u=1,9

Так как фактическое значение DW=1,34, можно считать, что существует автокорреляция в остатках.

Проверим условие не случайности значений остаточного ряда. Изобразим график остатков е_i на рисунке 3.

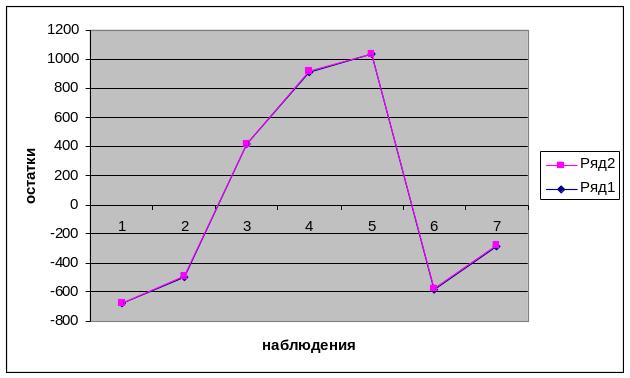
Рис. 6. График остатков

Следовательно, остатки не являются случайными.

Рассматривая в качестве прогнозной модели уравнение:

у = 1177801,733 + 0,005 ∙ х₁ – 11,276 ∙ х₂

оценим суммы затрат на ремонт в 2010 году.

Для вычисления прогнозных оценок У на основе построенной модели необходимо получить прогнозные оценки факторов Х₁ и Х₂.

Получим прогнозные оценки факторов на основе величины среднего абсолютного прироста САП.

Рассчитаем САП для Х₁:

САП=

САП= =56677,5

=474615+56677,5=531292,5

Следовательно, в 2010 году объём выпущенной продукции может составить 531292,5 тыс. руб.

Рассчитаем САП для Х₂:

САП= = – 142,17

Х_2пр.=102357–142,17=102214,83

Следовательно, в 2010 году среднегодовая стоимость основных средств может составить 102214,83 тыс. руб.

Вычислим прогнозную оценку суммы затрат на ремонт основных фондов:

у_пр=1177801,733 + 0,005 ∙ 531292,5 – 11,276 ∙ 102214,83 = 27883,77242

Значение у_пр= 27883,77242 тыс. руб. является точечной оценкой суммы затрат на ремонт при заданных значениях независимых переменных. Она указывает, какую сумму затрат на ремонт в среднем следует ожидать, если ситуация будет характеризоваться заданными значениями факторных показателей.

Отобразим на графике фактические данные, результаты расчётов и прогнозирования (рис. 4).

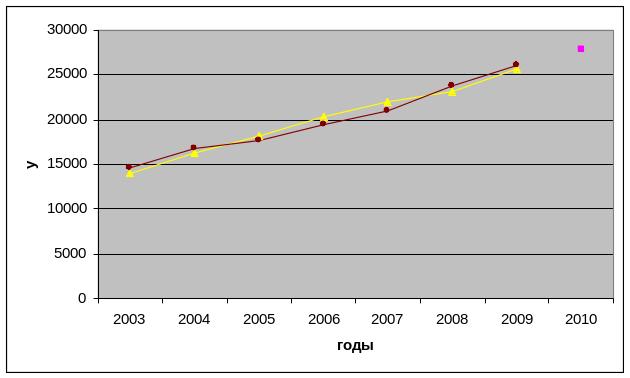
Рис. 7. Зависимость затрат на ремонт от среднегодовой стоимости основных средств и выпуска продукции

Построена эконометрическая модель зависимости суммы затрат на ремонт от среднегодовой стоимости основных средств и выпуска продукции. С использованием метода наименьших квадратов составлено уравнение регрессии:

у = 1177801,733 + 0,005 ∙ х₁ – 11,276 ∙ х₂

Параметры уравнения регрессии показывают, что:

– при увеличении фактора Х₁ – объема выпуска продукции – на 1 тыс. руб., величина затрат на ремонт увеличится в среднем на 0,005 тыс.руб. (или на 5 руб.). Это происходит в связи с тем, что увеличение выпуска продукции потребует дополнительной нагрузки на оборудование и прочие основные фонды и потребует дополнительных расходов на ремонт;

– при уменьшении среднегодовой стоимости основных средств на 1 тыс. руб., затраты на их ремонт уменьшатся на 11,276 тыс. руб. Это объясняется тем, что сокращение количества работающего оборудования и других основных фондов уменьшит необходимость в ремонте.

Так как множественный R=0,9841 больше 0,7, то связь между факторами х₁, х₂ и у – тесная.

Значение коэффициента детерминации R²=0,9685 показывает долю вариации результативного признака под воздействием изучаемых факторов. Следовательно, около 97% суммы затрат на ремонт зависят от включенных в модель факторов (среднегодовой стоимости основных средств и объёма продукции), а 3% зависят от факторов, не включенных в модель.

Нормированный R-квадрат свидетельствует, что при добавлении ещё одного фактора в модель, её обхват составит 95%. Таким образом, выбрано оптимальное число факторных признаков.

Полученное уравнение регрессии адекватно отражает статистическую зависимость между переменными.

Рассматривая в качестве прогнозной модели уравнение:

у = 1177801,733 + 0,005 ∙ х₁ – 11,276 ∙ х₂

оценили сумму затрат на ремонт в 2010 году.

Точечный прогноз предполагаемого значения суммы затрат на ремонт основных средств предприятия составил 27883,77242 тыс. руб.