Лабораторна робота №8

Тема: Підкидання монети по телефону з використанням імовірнісного криптування на основі дволистої функції Рабіна із секретом.

Мета: Отримати навички використання протоколу підкидання монети по телефону з використанням імовірнісного криптування на основі дволистої функції Рабіна із секретом.

Теоретичні відомості.

Протокол підкидання монети на основі дволистої функції Рабіна із секретом влаштований так.

• Аліса вибирає функцію дволисту функцію f і повідомляє про це Боба, втаївши секретний ключ K.

• Боб вибирає випадковий елемент x, обчислює 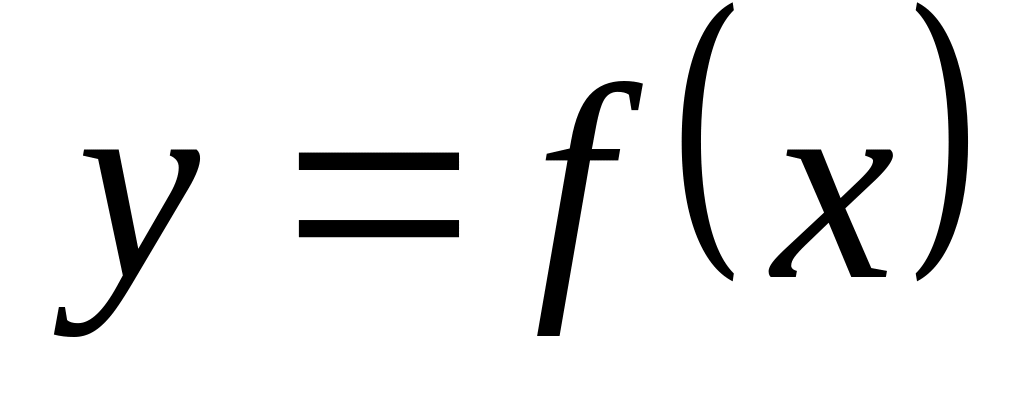і посилає у Алісі.

• Аліса за допомогою ключа К обчислює обидва прообрази

та елемента у: . Потім вибирає один із цих прообразів, скажімо і посилає його Бобові.

• Якщо 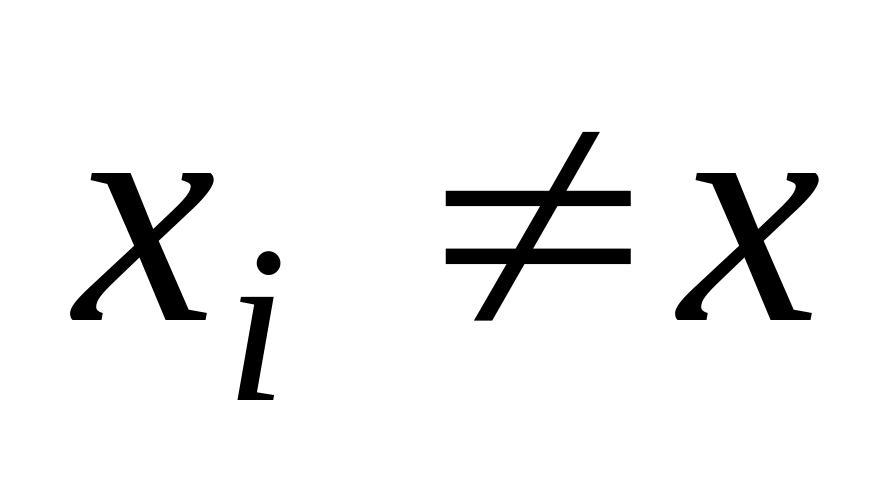, то Боб знає обидва прообрази елемента у і посилає їх Алісі. Аліса і Боб покладають г = 1.

• Якщо 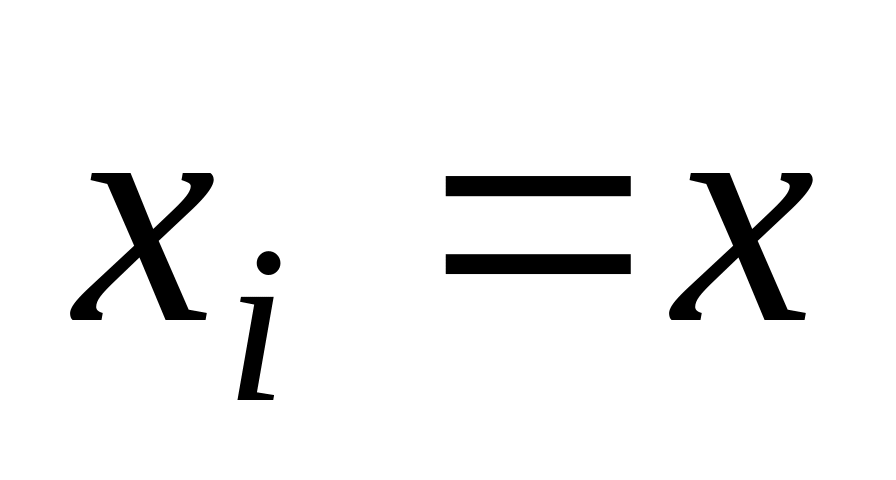, то Боб визнає, що не знає другого прообразу. В цьому випадку Аліса і Боб покладають г = 0.

• Аліса посилає Бобові секретний ключ К, і Боб перевіряє, що у має справді два прообрази.

Завдання:

1.Програмно реалізувати протокол підкидання монети по телефону з використанням імовірнісного криптування на основі дволистої функції Рабіна із секретом .

2.Визначити випадковий біт за допомогою розробленої програми, прийнявши за таємний ключ К=1591.

Лабораторна робота №9

Тема: Підкидання монети по телефону з використанням ймовірнісного криптування на основі телефонної книги

Мета роботи: Отримати навички використання протоколу підкидання монети по телефону з використанням ймовірнісного криптування на основі телефонної книги

Теоретичні відомості.

Особа А вибирає випадкового абонента B телефонному довіднику і покладає а=1, якщо в його прізвищі непарна кількість літер, або а=0, якщо парна. По телефону А повідомляє особі В телефонний номер вибраного абонента, залишаючи його прізвище у таємниці. Особа В називає свій випадковий біт b. Після цього особа А називає свій біт а, а також прізвище абонента, щоб особа В могла перевірити отриманий раніше телефонний номер і тим самим переконатися, що біт а був справді вибраний наперед.

Припускається, що за лічені секунди особа В не встигне знайти в довіднику абонента за його номером телефону. Також припускається, що в міській телефонній мережі абонентів з парною і непарною довжиною прізвища приблизно порівну.

Завдання.

1. Програмно реалізувати протокол підкидання монети по телефону з використанням ймовірнісного криптування на основі телефонної книги для кількості абонентів телефонної мережі, що дорівнює 20.

2. Визначити спільний біт двох абонентів, використовуючи запропоновану телефонну книгу.

Антоненко В В	63-40-91
Бобко Г В	63-77-95
Васніченко М С.	62-09-96
Григорчук І" Ю	62-99-66
Демко Л.С	34-18-84

Єременко О.К	34-42-96
Журавель Г.М	25-47-69
Заіребельний С В	52-11-78
Кабанчик БА.	72-3-86
Леснж F.B.	63-70-37
Максимів Ю.В	33-53-32
Наумчик CM	72-18-22
Олійник Г.Л.	62-63-02
Пастух В 11	63-97-24
РоманенкоЛ П	62-36-03
Семчишин ЇМ	72-74-05
Тарас юк А.Г.	62-38-69
Уденко A.M.	62-31-64
Федишин Д.Г	62-24-58
ХомснкоСД,	42-52-20
Шварц АП	52-59-17

Лабораторна робота №10

Тема: Заочна гра в карти з використанням функції RSA

Мета роботи: Отримати навички використання протоколу заочної гри в карти з використанням функції RSA

Теоретичні відомості

Протокол використовує довільну комутативну криптосистему. Алгоритми шифрування і дешифрування Аліси позначимо через Е_А і D_A , а Боба — через Е_в і D_B. Комутативність криптосистеми означає, що для будь-якого повідомлення М справедлива рівність

Е_В(Е_А(М)) = Е_А(Е_В(М)).

Прикладом такої системи є модифікація RSA, де модуль n учасники вибирають спільно, а шифруючі і дешифруючі ключі e і d — таємно одне від другого. Учасник X вибирає пару із шифруючого ключа е_X і дешифруючого d_X з властивістю і здійснює шифрування та дешифрування за формулами

,

Опис протоколу.

• Аліса і Боб досягають згоди про кодування карт словами і домовляються яка саме комутативна криптосистема буде використовуватись.

• Обидвоє таємно одне від другого вибирають собі шифруючий та дешифруючий ключі.

' Аліса зашифровує повідомлення , перемішує випадковим чином криптотексти і посилає їх Бобові.

• Боб вибирає випадкові п'ять криптотекстів, і посилає їх назад Алісі. Це карти, якими буде грати Аліса. Боб не може визначити карт Аліси, бо не знає її ключа.

■ Із карт, що залишилися, Боб вибирає ще п'ять для себе. Боб вибрав карти у зашифрованому вигляді і тепер повинен довідатись, які це власне карти. Це він може зробити лише за допомогою Аліси, але повинен подбати, щоб при цьому його карти не відкрилися і їй.

• Боб зашифровує відібрані за допомогою власного ключа і криптотексти посилає Алісі.

• Аліса дешифрує отримані криптотексти і повертає Бобові результат. Аліса, яка не знає ключів Боба, не може визначити його карти.

Боб дешифрує надіслані Алісою і отримує свою п'ятірку карт .

В кінці гри Аліса і Боб обмінюються ключами і перевіряють, що ніхто з них не хитрував.

Завдання.

1. Програмно реалізувати протокол заочної гри з використанням RSA.

2. Реалізувати роздачу карт при n=3551; e=1021; d=1237.