
МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ
Національний університет "львівська політехніка"
ІНСТИТУТ ПІДПРИЄМНИЦТВА ТА ПЕРСПЕКТИВНИХ ТЕХНОЛОГІЙ
КРИПТОГРАФІЧНІ ПРОТОКОЛИ
МЕТОДИЧНІ ВКАЗІВКИ
До виконання лабораторних робіт з курсу "Математичні основи захисту інформації"
для студентів базового напряму 6.050101 "Комп’ютерні науки "
Затверджено на засіданні кафедри "Інформаційних систем і технологій " Протокол № _ від __________
Львів 2013
Криптографічні протоколи: Методичні вказівки до виконання лабораторних робіт з курсу «Математичні основи захисту інформації» для студентів базового напрямку підготовки 6.050101 «Комп’ютерні науки»-Львів. Національний університет "Львівська політехніка". 2013. - 15 с.
Укладач: Волошин В.В., канд. фіз.-мат. наук, доцент.
Відповідальний
за випуск: __________________________________________.
Рецензенти: _______________________________________
__________________________________________________________.
Лабораторна робота №1
Тема: Експоненційний обмін ключем
Мета роботи: Отримати навички використання протоколу експоненційного обміну ключем.
Теоретичні відомості
Учасниками цього протоколу є дві особи А та В, які, спілкуючись через канал, що ймовірно прослуховується, хочуть домовитись про спільний таємний ключ.
- Особа А вибирає велике просте число р та первісний корінь g за модулем р, і не роблячи з цього жодної таємниці, посилає р i g особі В.
- А вибирає випадкове число а в межах від 1 до р - 1, а В - випадкове число b в тих же межах.
- А обчислює a mod p і посилає це значення В, а В обчислює g mod p і теж посилає А.
- А і В обчислюють одне і те ж число
![]() ,
яке і приймають
в якості ключа.
,
яке і приймають
в якості ключа.
Завдання.
Програмно реалізувати протокол обміну ключем абонентів А та В.
Реалізувати обмін при р = 23, g = 5, а = 15, b = 18.
Лабораторна робота №2
Тема: Цифровий підпис у системі RSA
Мета роботи: Отримати навички використання протоколу цифрового підпису, використовуючи систему RSA.
Теоретичні відомості.
В системі RSA
кожен абонент X
має пару ключів
— загальновідомий відкритий
![]() і
таємний
і
таємний
![]() ,
який знає лише
X
і ніхто інший.
Таким чином, будь-хто може скористатися
Алгоритмом шифрування
,
який знає лише
X
і ніхто інший.
Таким чином, будь-хто може скористатися
Алгоритмом шифрування
![]() абонента Х, але тільки він сам володіє
алгоритмом дешифрування
абонента Х, але тільки він сам володіє
алгоритмом дешифрування
![]() .
Важливим є
виконання таких співвідношень для
довільного повідомлення М.
.
Важливим є
виконання таких співвідношень для
довільного повідомлення М.
![]() .
.
Ці співвідношення виражають той факт, що шифруюче відображення дешифруюче є взаємно оберненими.
Припустимо тепер,
що Аліса хоче послати Бобові повідомлення
М таким чином,
шоб той був певен, що повідомлення
справді послане Алісою,
а не її суперницею Агнесою. Для цього
пропонується такий протокол, в якому
![]() та
та
![]() — алгоритми шифрування та
дешифрування Аліси та Боба.
— алгоритми шифрування та
дешифрування Аліси та Боба.
Відкритий ключ; е,п.
Таємний ключ: d
Алгоритм шифрування
Е у системі
RSA
полягає у піднесенні М
до степеня
![]() ,
де М –
блок відкритого
тексту, який розглядається як елемент
кільця Zn
і може підноситись до степеня за модулем
п .
,
де М –
блок відкритого
тексту, який розглядається як елемент
кільця Zn
і може підноситись до степеня за модулем
п .
Записуємо це так:
![]() .
.
В результаті
отримується блок криптотексту С
= Е(М), який
також є цифровим записом якогось елемента
кільця
![]() .
.
Дешифрування. Алгоритм дешифрування D блоку криптотексту С полягає у піднесенні С до степеня d, тобто
![]() .
.
Аліса обчислює
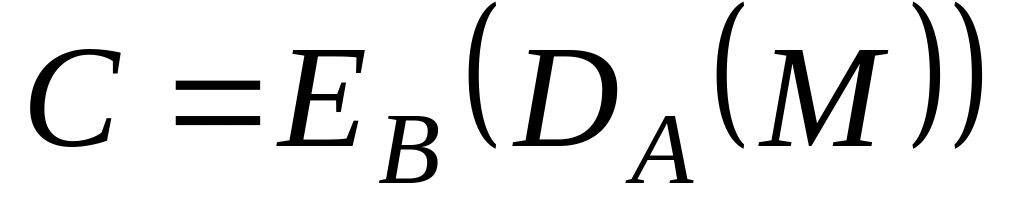 і посилає
С Бобові.
і посилає
С Бобові.Боб, отримавши С, обчислює
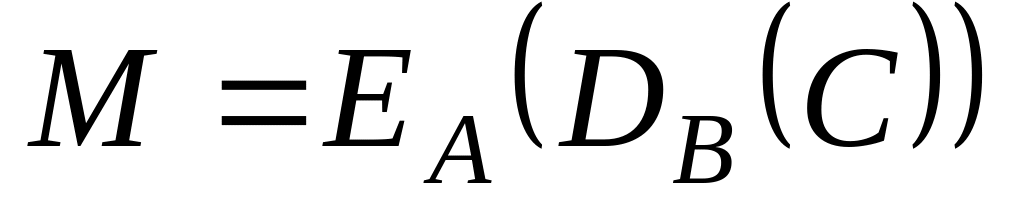 .
.
Загальна схема криптографічних протоколів. Описана криптосистема забезпечує як достовірність повідомлення, так і його конфіденційність. Є системи власне цифрового підпису, метою яких є забезпечення лише достовірності. Такі системи вкладаються у схему, що включає в себе такі складові:
Ймовірнісний алгоритм генерування ключів. Кожен абонент А отримує пару
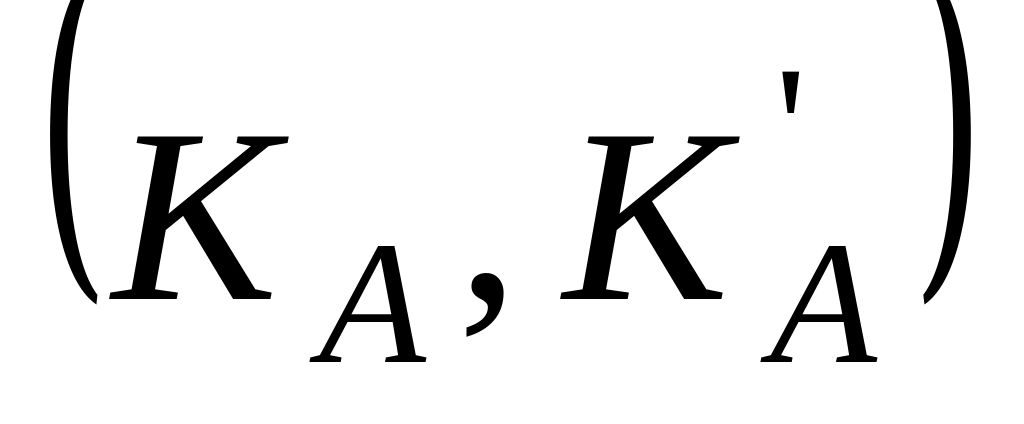 ,
де КА
— відкритий,
а К'А
— таємний
ключі.
,
де КА
— відкритий,
а К'А
— таємний
ключі.Алгоритм підписування SIGN, який отримавши на вхід довільне повідомлення М та таємний ключ
 ,
продукує слово
,
продукує слово
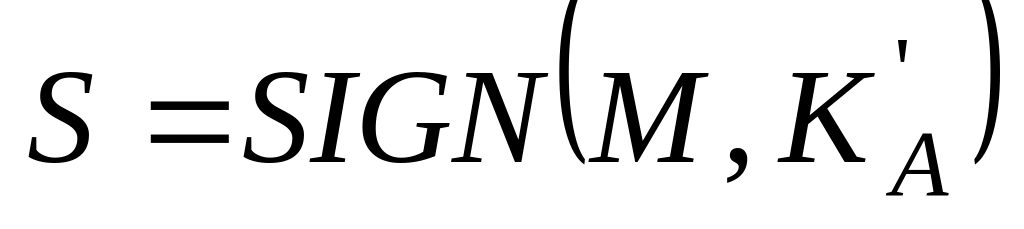 в деякому алфавіті,
яке називається підписом
абонента А
на повідомленні
М. Коли
А хоче
послати комусь повідомлення М
із запевненням,
що воно відправлене саме ним, то посилає
пару (М ,S).
в деякому алфавіті,
яке називається підписом
абонента А
на повідомленні
М. Коли
А хоче
послати комусь повідомлення М
із запевненням,
що воно відправлене саме ним, то посилає
пару (М ,S).Алгоритм підтвердження підпису CHECK, який є до послуг будь-кого, хто забажає перевірити, що підпис S повідомлення М належить саме власникові відкритого ключа КА. Перевірка вважається успішною, якщо CHECK(KA,M,S)=1. Для будь-якого повідомлення М і для кожної пари ключів (К, К') має виконуватись співвідношення CHECK(K,M,SIGN(M,K'))= I.
Завдання.
1 Програмно реалізувати цифровий підпис у системі RSA.
2. Підписати повідомлення : Love is the bird, she needs to fly, let all the hurt inside of you die, якщо n=3551; e=1021; d=1237. Перевірити отриманий ПІДПИС.
Лабораторна робота №3
Тема: Система цифрового підпису Ель Гамала
Мета: Отримати навички використання протоколу цифрового підпису на основі системи Ель Гамала
Теоретичні відомості
Генерування ключів.
Вибирають велике
просте р, а
також число g,
1 < g
< p-1,
яке має в мультиплікативній
групі
![]() великий
порядок. В ідеальному випадку g
є первісним
коренем за модулем р.
Числа р
і g
не є таємницею
і перебувають в загальному
користуванні. Кожен абонент вибирає
собі випадкове число а
в
проміжку від
1 до р-1,
і обчислює
великий
порядок. В ідеальному випадку g
є первісним
коренем за модулем р.
Числа р
і g
не є таємницею
і перебувають в загальному
користуванні. Кожен абонент вибирає
собі випадкове число а
в
проміжку від
1 до р-1,
і обчислює
![]() .
.
Відкритий ключ: р, q, h.
Таємний ключ: а.
Підписування. Аліса підписує повідомлення М у послідовності:
вибирає випадкове число
 ;
;обчислює
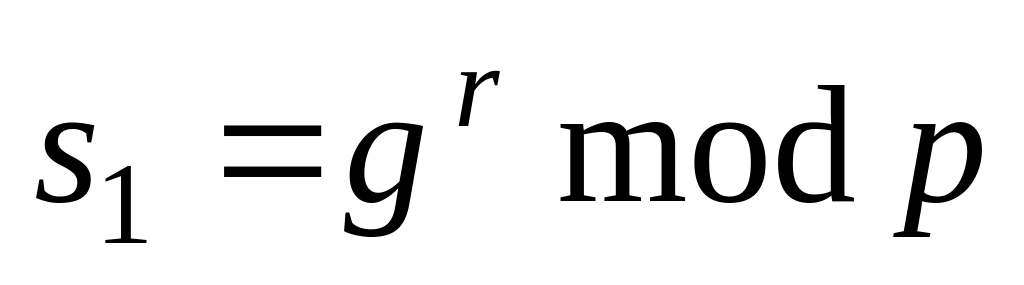 ;
;обчислює
 ;
;обчислює
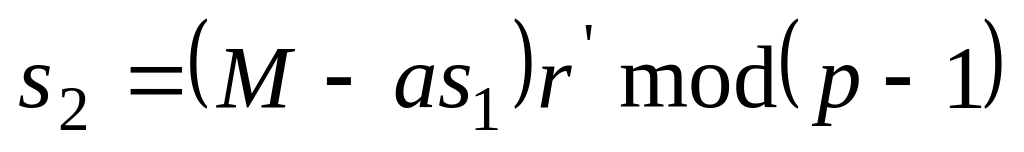 ;
;покладає у якості підпису
 .
.
Підтвердження
підпису. Боб
перевіряє, чи
![]() .
.
Завдання:
1.Програмно реалізувати систему цифрового підпису Ель Гамала.
2. Реалізувати процедуру цифрового підпису на повідомленні "If I could turn back the hands of time "при таких ключах ; p=43;g=41;h=11.
Лабораторна робота №4
Тема: Система Шнорра цифрового підпису
Мета роботи: Отримати навички використання протоколу цифрового підпису на основі системи Шнорра
Теоретичні відомості.
Вибирають велике
просте число р
таке, що р
- 1 має досить
великий простий
дільник
q.
Вибирають також число h,
яке не
дорівнює 1, але
![]() .
Параметри
p,q,h
не
становлять таємниці і є спільними для
всіх абонентів
мережі. Особа
А вибирає
випадкове число а
в діапазоні
від 1 до q
- 1 і обчислює
число
.
Параметри
p,q,h
не
становлять таємниці і є спільними для
всіх абонентів
мережі. Особа
А вибирає
випадкове число а
в діапазоні
від 1 до q
- 1 і обчислює
число
![]() .
ЇЇ
ключі формуються так.
.
ЇЇ
ключі формуються так.
Відкритий ключ:
![]() таке, що
таке, що
![]() /
/
Таємний ключ: а.
Підписування. Алгоритм підписування використовує деяку вкорочуючу функцію f. Щоб виробити свій підпис S для повідомлення М, особа А:
вибирає випадкове число r в діапазоні від 0 до q - 1;
обчислює X = hr mod p;
обчислює
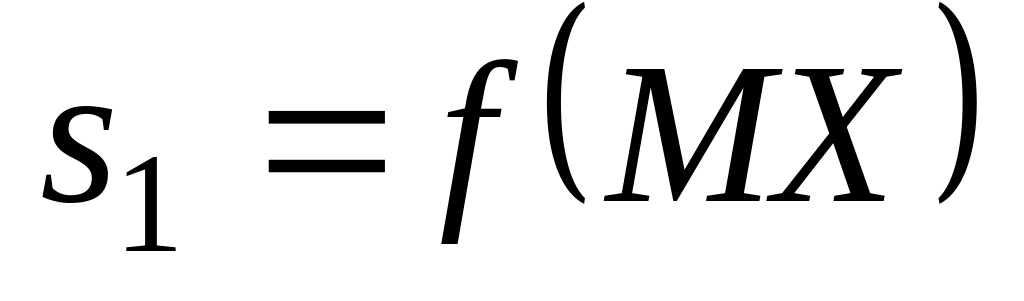 ,
де MX
позначає
результат злиття М
і
X
в один
текст;
,
де MX
позначає
результат злиття М
і
X
в один
текст;обчислює
 ;
;утворює .
Підтвердження підпису. Отримавши повідомлення М із підписом , особа В:
обчислює
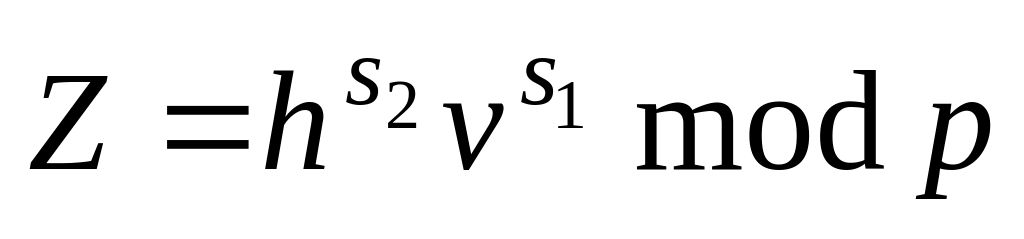 ;
;перевіряє, чи
 .
.
Завдання.
Програмно реалізувати систему Шнорра цифрового підпису.
Реалізувати процедуру цифрового підпису на повідомленні М = <Тема>, при р = 997, h = 565, а = 111. Вкорочуючою є функція, яка сумує коди всіх символів повідомлення і з утвореного числа бере перші дві цифри.
