§ 2. Выборки элементов

Пусть имеем некоторое множество из п элементов а₁, а₂, а₃, ..., а_п. Из этого множества можно образовать разные выборки, каж­дая из которых имеет r элементов

.

Выборки могут быть упорядоченными — размещениями. Напри­мер, из элементов a, b и с можно образовать такие выборки-размещения по 2 элемента:

ab, ba, са,

ac, be, cb.

Этих выборок 6, и они одна от другой отличаются либо элемента­ми, либо их порядком.

Попробуем из 4 элементов a, b, c и d образовать подобные выбор­ки по 3. Вот они:

abc,	bac,	cab,	dab,
abd,	bad,	cba,	dba,
acb,	bca,	cad,	dac,
adb,	bda,	cda,	dca,
acd,	bcd,	cbd,	dbc,
adc,	bdc,	cdb,	dcb.

Всего 24 выборки. В обоих примерах мы имеем дело с выборками, которые называются размещениями. В первом случае мы имеем дело с размещениями из 3 элементов по 2, во втором — из 4 по 3.

Размещениями из п элементов по т называются такие выборки, которые, имея по т элементов, выбранных из числа данных п элементов, отличаются одна от другой либо составом элементов, либо порядком их расположения.

Число размещений из п элементов по т договоримся обозначать . Это число определяется следующим образом:

. (2.9)

С помощью этой формулы решим задачу.

15. Допустим, в высшей лиге по футболу 18 команд. Борьба идет за золотые, серебряные и бронзовые медали. Скольки­ми способами медали могут быть распределены между командами?

Решение.

Ясно, что нужно найти число размещений . По формуле (2.9)

.

Если кто-то в начале сезона, не зная, как укомплектованы и под­готовлены команды, ручается, что золотые медали будут у киевских динамовцев, серебряные — у араратовцев, а бронзовые — у мо­сковских спартаковцев, то он смельчак — называет одну комбина­цию из 4896 возможных. (Возможны случаи, когда команды делят места.)

Ответ: 4896.

Если в формуле (2.9) m = n, то — число таких размещений, которые отличаются только порядком расположения элементов, но не самими элементами. Такие размещения называются переста­новками. Их число по формуле (2.9)

.

(2.10)

Число п может принимать не только натуральные значения, оно может также равняться нулю. Пустое множество (выборка) явля­ется подмножеством любого множества, и естественно считать, что оно может быть упорядочено только одним способом. Принято счи­тать, что 0! = 1.

На практике не всегда важен порядок расположения в выбор­ках. Например, если в полуфинале первенства России по шахматам участвуют 20 шахматистов, а в финал из них попадут только трое, то участнику безразлично (если им не руководят соображения пре­стижа), какое из первых трех мест занять. Ведь были случаи, когда занявший третье место в полуфинале в финале был первым.

Если требуется установить, сколькими способами может образо­ваться финальная тройка, то надо посчитать только те выборки из 20 элементов по 3, которые одна от другой отличаются хотя бы одним элементом.

Число сочетаний из п элементов по т обознача­ется

. (2.11)

Применяя эту формулу для решения задачи о шахматистах, получим число возможных финальных троек

.

Формулы (2.9), (2.10) и (2.11) могут быть применены для опреде­ления числа случайных событий — результатов испытаний или на­блюдений.

Задачи

15. На тренировках занимаются 12 баскетболистов. Сколько может быть образовано тренером разных стартовых пятерок?

Решение.

Так как при составлении стартовой пятерки тренера интересует только состав пятерки, то достаточно определить число сочета­ний из 12 элементов по 5

.

Ответ: 792.

15. Сколькими способами можно расположить на шахматной доске 8 ладей так, чтобы они не могли взять друг друга?

Решение.

Ясно, что в этом случае на каждой горизонтали и каждой вертикали шахматной доски мо­жет быть расположено только по одной ладье. Число возмож­ных позиций — число переста­новок из 8 элементов:

.

Ответ: 40320.

15. Для полета на Марс необходимо укомплектовать следующий экипаж космического корабля: командир корабля, первый его помощник, второй помощник, два бортинженера и один врач. Командующая тройка может быть отобрана из числа 25 готовящихся к полету летчиков, два бортинженера — из числа 20 специалистов, в совершенстве знающих устройство космического корабля, и врач — из числа 8 медиков. Сколькими способами можно укомплектовать экипаж исследователей космоса?

Решение.

При выборе командира и его помощников, важно определить; какой из военных летчиков лучше других справляется с теми или иными функциями в управлении кораблем. Значит, здесь важен не только персональный состав командующей тройки, но и соответ­ствующая расстановка подобранных людей. Поэтому ясно, что ко­мандующая тройка может быть укомплектована способами.

Обязанности у обоих бортинженеров примерно одинаковые. Они могут выполнять их по очереди. Следовательно, пара борт­инженеров может быть укомплектована способами. Аналогич­ное положение и с врачом — его можно подобрать способами.

В силу формулы (3.2) весь экипаж может быть укомплектован

способами.

Ответ: 20 976 000.

15. Сколькими способами можно расставить на полке 8 книг, среди них 2 книги одного автора, которые при любых перестановках должны стоять рядом?

Решение.

Условно будем считать две книги одного автора единой книгой. Тогда количество способов расстановки условных 7 книг на полке будет равно числу перестановок из 7 элементов:

.

Но в каждой такой перестановке книги одного автора можно поменять местами, поэтому общее число способов расстановки книг на полке будет в 2 раза больше, т.е. .

Ответ: 10 080 способами.

15. Сколькими способами можно закрасить 6 клеток таким образом, чтобы 3 клетки были красными, а 3 оставшиеся были закрашены (каждая своим цветом) белым, черным или зеленым?

Решение.

Условно будем считать, что все клетки закрашиваем разными цветами. Это можно сделать способами. Но в каждой такой перестановке три клетки одного цвета и их можно переставить способами, следовательно, общее число способов будет меньше в 6 раз, т.е. способов.

Ответ: 120.

15. Докажите, что .

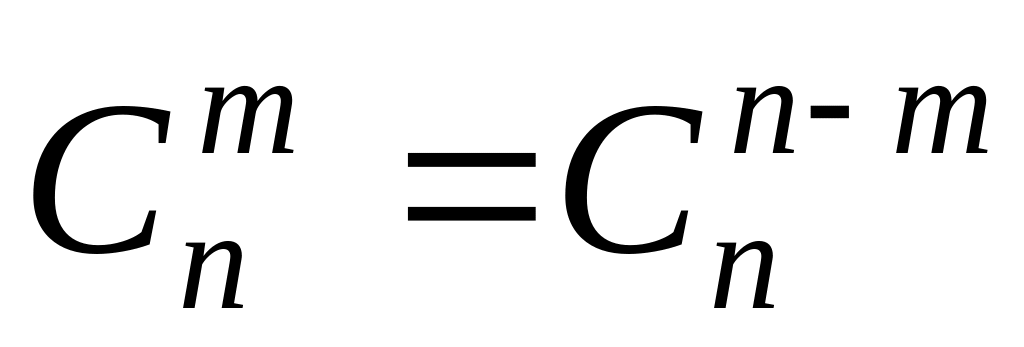Решение.

По определению, ,

,

а, следовательно, .

15. Докажите равенство Паскаля:

.

Решение.

Преобразуем левую часть равенства:

15. Сколько разных трехзначных чисел можно составить из цифр 1, 2, 3, 4 и 5 при условии, что ни одна цифра не повторяется?

Решение.

Выбираем 3 цифры из 5 данных; порядок выбора имеет значение:

чисел.

Ответ: 60.

15. Сколько существует семизначных телефонных номеров, в которых все цифры различные и первая цифра отлична от нуля?

Решение.

Выбираем из 10 цифр семь, причем первый выбор делается из 9 цифр(без нуля).

Используя метод исключения лишних вариантов, получаем:

номеров.

Ответ: 544 320.