Вычитание

А –– «наугад остановленный мужчина –– брюнет»,

В — «наугад остановленный мужчина — высокого роста»,

С — «наугад остановленный мужчина — невысокий брюнет».

Нетрудно заметить, что со­бытие С означает то, что про­изошло А, но не произошло В. Принято такое событие С считать разностью событий А и В.

Вообще, разностью событий А и В называется событие С, состоя­щее в том, что произошли те элементарные события, которые вхо­дят в А, но не входят в В. В таком случае пишем:

С=А—В. (5.7)

Если это определение выразить символами уже известных нам соотношений, то

. (2.6)

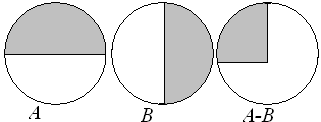
Рис. 5.

Пусть события А и В представлены подмножествами одного и того же множества элементарных событий Е, A = {e₁, е, е₃, е₄} и В = {е₂, е₄}. Тогда разность событий А — В представляется подмно­жеством {е₁, е₃}.

Геометрически разность событий изображена на рисунке 5.

Рассмотрим следующую задачу.

15. Пусть A, В и С — события. Доказать, что А (В — С) = АВ — АС.

На языке теории множеств . Получим отсюда как следствие, что

Теперь пусть . Приведем рассуждения в обрат­ном порядке:

Следовательно, равенство А (В – С) = АВ – АС действительно имеет место, поскольку множества А (В – С) и АВ – АС состоят из одних и тех же элементарных событий.

Задачи

15. Событие А – «попадание в мишень»,

событие В – «попадание в мишень первым выстрелом».

В чем состоит событие А – В?

Решение.

По определению, событие А – В состоит в попадании в мишень не первым выстрелом.

Ответ: попадание не первым выстрелом.

15. Событие А – «получение достаточной для сдачи экзамена оценки»,

событие В – «получение пятерки».

В чем состоят события А – В, , .

Решение.

Событие А – В – получение 4 или тройки;

событие – получение пятерки;

событие – невозможное событие(по определению).

Ответ: получение 4 или 3; получение пятерки; невозможное событие.

Глава 2. Наука о подсчете числа комбинаций – комбинаторика

Комбинаторикой называется область математики, в которой изучаются вопросы о том, сколько различных комбинаций, подчи­ненных тем или иным условиям, можно составить из элементов, принадлежащих заданному множеству. Иногда комбинаторику рассматривают как введение в теорию вероятностей, поскольку методы комбинаторики очень помогают в теории вероятностей осуще­ствить подсчет числа возможных исходов и числа благоприятных исходов в разных конкретных случаях.

В теории вероятностей принято говорить не о комбинациях, а о выборках. Поэтому мы будем придерживаться термина «выборка».

В комбинаторике рассматриваются виды выборок — перестановки, размещения, сочетания. Как увидим дальше, выборки могут в отличие от множеств включать повторно тот или иной элемент.

§ 1. Общие правила комбинаторики

Рассмотрим два общих правила, с помощью которых решается большинство задач комбинаторики, — правило суммы и правило произведения.

Допустим, в ящике имеется п разноцветных шариков. Произ­вольным образом вынимаем один шарик. Сколькими способами мож­но это сделать? Конечно, п. Теперь эти п шариков распределим по двум ящикам: в первом — т шариков, во втором — k. Произвольно из какого-нибудь ящика вынимаем один шарик. Сколькими разными способами можно это сделать? Из первого ящика шарик мож­но вынуть т разными способами, из второго — k разными способа­ми. Всего п = т + k способами. (2.7)

Если некоторый объект А можно выбрать т способами, а объект В — k способами (не такими, как A), то объект «либо A, либо В» можно выбрать т + k способами»

Это так называемое правило суммы.

Перейдем к правилу произведений. Рассмотрим следующую задачу.

15. Сколько можно записать двузначных чисел в десятич­ной системе счисления?

Решение.

Поскольку число двузначное, число десятков может принимать одно из девяти значений: 1, 2, 3, 4, 5, 6, 7, 8, 9. Число единиц может принимать те же значения и может, кроме того, быть равным нулю.

Если цифра десятков 1, цифра единиц может быть 0, 1, 2, ... — всего 10 значений. Если цифра десятков — 2, то вновь цифра еди­ниц может быть равна 0, 1, 2, ... . Всего получаем 90 двузначных чисел.

Ответ: 90 чисел.

Обобщим полученный результат. Пусть данное множество из п = т + k элементов разбито на два подмножества, состоящие соответственно из т и k элементов. Пусть из подмножества, содержа­щего т элементов, выбирается один элемент и независимо из под­множества, содержащего k элементов, выбирается один элемент. Спрашивается, сколько различных пар элементов при этом образу­ется?

Ответ на поставленный вопрос дает таблица.

Таким образом, если общее число всевозможных пар обозначим N, то

N = mk. (2.8)

Сформулируем теперь правило произведений.

Если объект А можно выбрать т способами, а после каждого такого выбора другой объект В можно выбрать (независимо от вы­бора объекта A) k способами, то пары объектов А и В можно вы­брать mk способами.