
- •Содержание
- •Предисловие
- •Избранные задачи теории вероятностей
- •Глава 1. Случайные события и операции над ними
- •§ 1. Случайное событие
- •§ 2. Множество элементарных событий
- •§ 3. Операции над событиями Сложение
- •Умножение
- •Вычитание
- •Глава 2. Наука о подсчете числа комбинаций – комбинаторика
- •§ 1. Общие правила комбинаторики
- •§ 2. Выборки элементов
- •§ 3. Выборки с повторениями
- •Глава 3. Вероятность события
- •Глава 4. Операции над вероятностями
- •§ 1. Вероятность суммы несовместных событий
- •§ 2. Вероятность суммы совместных событий
- •§ 3. Условные вероятности
- •§ 4. Вероятность произведения независимых событий
- •§ 5. Формула полной вероятности
- •Глава 5. Независимые повторные испытания
- •§ 1. Формула Бернулли
- •§ 2. Формула Муавра – Лапласа
- •Вычислить X;
- •По таблице в приложении 1 найти значение φ(X);
- •Вычислить по формуле (2.28). Задачи
- •§ 3. Формула Пуассона
- •§ 4. Формула Лапласа
- •Вычислить m1 и m2 по формулам
- •По таблице найти значения ф(x1) и ф(x2);
- •Вычислить ф(x2) – ф(x1). Задачи
- •Возникновение и развитие теории вероятностей как науки
- •Литература
§ 2. Вероятность суммы совместных событий
Пусть т — число равновозможных элементарных событий, благоприятствующих событию A, k — число равновозможных элементарных событий, благоприятствующих событию В. Допустим, что среди упомянутых т + к событий содержится l таких, которые благоприятствуют и событию A, и событию В. Если п — общее число равновозможных элементарных событий, образующих полную группу, то согласно формуле (2.16)
,
,
![]() .
.
Запись A + В означает: «произойдет или событие A, или В, или и то и другое вместе». Но такому событию благоприятствуют (т + k — l) элементарных событий. Поэтому по формуле (4.1) находим:
![]() .
.
Подставляя значение, получим:
Р(А + В) = Р(А) + Р(В) — Р (АВ). (2.19)
Ясно, что эта формула представляет собой обобщение формулы (2.18). На основании равенства (2.19) формулируем правило.
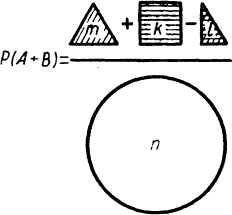
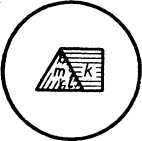
Рис. 9.
Вероятность суммы двух совместимых событий равна сумме вероятностей этих событий без вероятности их совместного осуществления.
Геометрическая интерпретация формулы (2.19) дается на рисунке 9, где m, k, l, n представляют величины площадей нарисованных фигур.
Задачи
Задача 66. Подбрасываем две монеты. Какова вероятность выпадения хотя бы одного герба?
Решение.
Обозначим события:
А — «появление герба при подбрасывании первой монеты»,
В — «появление герба при подбрасывании второй монеты».
Нам надо определить вероятность события С = А + В. Так как А и В — совместимые события, то
Р (С) = Р (А + В) = Р (А) + Р (В) — Р (АВ).
Ясно, что
![]() ,
,
![]() ,
,
![]() .
Отсюда
.
Отсюда
![]() .
.
Ответ: .
Бросают две игральные кости. Какова вероятность появления хотя бы одной шестерки?
Решение.
Обозначим события:
A — «появление шестерки при бросании первой кости»,
В — «появление шестерки при бросании второй кости».
Нам надлежит определить вероятность события С = А + В.
Р (С) = Р (А + В) = Р (А) + Р (В) - Р (АВ).
Ясно, что
![]() ,
,
![]() ,
,
![]() .
.
Тогда
![]() .
.
Ответ:
![]() .
.
A, В и С — совместимые события. Доказать:
Р (А + В + С) = Р (А) + Р(В) + Р(С) — Р (АВ) — Р (АС) — Р (ВС) + Р (ABC).
Решение.
Обозначим А + В = D. Тогда
Р (А + В + С) = Р (D + С) = Р (D) + Р(С) – Р (DC) = Р (А + В) + Р (С) —
– Р ((А + В) С) = Р (А) + Р(В) — Р (АВ) + Р(С) — Р (АС + ВС)= Р (А) + Р(В)+ + Р (С)—Р (АВ) — (Р (АС) + Р (ВС) — Р (АСВС)) = Р(А) + Р(В) +
+Р(С) – Р (АВ) – P (АС) — Р (ВС) + Р (ABC), ибо
АСВС = AВС.
§ 3. Условные вероятности
Из ящика, в котором а белых и b черных шаров, наугад вынимаются последовательно один за другим два шара. Рассмотрим события:
А — «первый шар белый»,
В — «второй шар белый».
Понятно,
что
![]() .
Какова же вероятность события В?
.
Какова же вероятность события В?
Если событие А произошло, то среди оставшихся а + b — 1 шаров только
а —
1 белых, поэтому вероятность того, что
второй шар белый
![]() .
Если же А
не
произошло, то среди оставшихся шаров
белых а,
поэтому вероятность того, что второй
шар белый
.
Если же А
не
произошло, то среди оставшихся шаров
белых а,
поэтому вероятность того, что второй
шар белый
![]() .
Мы столкнулись с ситуацией, когда
вероятность появления события В
зависит
от того, произошло или не произошло
событие A.
В таком случае говорим, что событие В
зависит
от события A,
а вероятность появления события В
условная.
.
Мы столкнулись с ситуацией, когда
вероятность появления события В
зависит
от того, произошло или не произошло
событие A.
В таком случае говорим, что событие В
зависит
от события A,
а вероятность появления события В
условная.
Найдем способ вычисления таких вероятностей.
Условную вероятность появления события В, если событие А произошло, будем обозначать Р (В/А).
Пусть из п равновозможных событий А1, A2, ..., Ап, составляющих полную группу,
событию А благоприятствуют т событий,
событию В благоприятствуют k событий,
событию АВ благоприятствуют r событий
(понятно,
что
![]() ).
Если
событие А
произошло,
то это означает, что наступило одно из
событий Aj,
благоприятствующих событию A.
При этом условии событию В
благоприятствуют
r
и
только r
событий
Aj
благоприятствующих
АВ.
Таким
образом:
).
Если
событие А
произошло,
то это означает, что наступило одно из
событий Aj,
благоприятствующих событию A.
При этом условии событию В
благоприятствуют
r
и
только r
событий
Aj
благоприятствующих
АВ.
Таким
образом:
![]() ,
,
![]() ,
,
т. е.
![]() .
(2.20)
.
(2.20)
На основании (2.20) формулируем правило умножения вероятностей.
Вероятность произведения двух событий равна произведению вероятности одного из этих событий на условную вероятность другого при условии, что первое произошло.
Замечание. Формулы (2.20) имеют смысл в том случае, если имеют смысл события А/В и В/А. А они имеют смысл тогда, когда события A и B совместимы.
Задачи
В ящике а белых и b черных шаров. Последовательно вынимаются два шара. Какова вероятность того, что оба они белые?
Решение.
Обозначим события:
A — «первый шар белый»,
В — «второй шар белый».
Нам надлежит найти Р (АВ). Имеем:
![]() ,
,
![]() .
.
Согласно формуле (5.3) находим:
![]() .
.
Ответ:
![]() .
.
Из колоды в 32 карты наугад одну за другой вынимают две карты. Найти вероятность того, что:
а) вынуты два валета;
б) вынуты две карты пиковой масти;
в) вынуты валет и дама.
Решение.
Обозначим события:
A — «первая карта — валет»,
В — «вторая карта — валет»,
С — «первая карта — пиковой масти»,
D — «вторая карта — пиковой масти»,
Е — «вторая карта — дама».
Нам следует найти Р (АВ), Р (CD) и Р (АЕ).
По формуле (5.3)
![]() ;
;
![]() ;
;
![]() ;
;
![]() ,
тогда
,
тогда
![]() ;
;
![]() ,
тогда
,
тогда
![]() ;
;
![]() ,
тогда
,
тогда
![]() .
.
Ответ:
![]() ;
;
![]() ;
;
![]() .
.
Доказать:
![]() .
.
Пусть
А1А2
=
В. Тогда
![]() .
По
формуле (5.3)
.
По
формуле (5.3)
![]() .
.
Еще раз применяем формулу (5.3):
![]() .
.
