Двоичная система счисления — позиционная система счисления с основанием 2. Благодаря непосредственной реализации в цифровых электронных схемах на логических вентилях, двоичная система используется практически во всех современных компьютерах и прочих устройствах на их основе.

Содержание

  [убрать] 

1 Двоичная запись чисел

1.1 Натуральные числа

1.2 Отрицательные числа

1.3 Дробные числа

2 Сложение, вычитание и умножение двоичных чисел

3 Преобразование чисел

3.1 Преобразование двоичных чисел в десятичные

3.1.1 Преобразование дробных двоичных чисел в десятичные

3.2 Преобразование методом Горнера

3.2.1 Перевод дробных чисел методом Горнера

3.3 Преобразование десятичных чисел в двоичные

3.3.1 Преобразование дробных десятичных чисел в двоичные

4 Применения

4.1 В цифровых устройствах

4.2 В английской системе мер

5 Обобщения

6 История

7 Интересные факты

8 См. также

9 Примечания

10 Ссылки

Двоичная запись чисел[править | править исходный текст]

В двоичной системе счисления числа записываются с помощью двух символов (0 и 1). Чтобы не путать, в какой системе счисления записано число, его снабжают указателем справа внизу. Например, число в десятичной системе 5₁₀, в двоичной 101₂. Иногда двоичное число обозначают префиксом 0b, например 0b101.

В двоичной системе счисления (как и в других системах счисления, кроме десятичной) знаки читаются по одному. Например, число 101₂ произносится «один ноль один».

Натуральные числа[править | править исходный текст]

Натуральное число, записываемое в двоичной системе счисления как  , имеет значение:

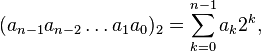
где:

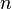•  — количество цифр (знаков) в числе,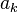

•  — цифры из множества {0,1},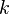

•  — порядковый номер цифры.

Отрицательные числа[править | править исходный текст]

Отрицательные двоичные числа обозначаются так же как и десятичные: знаком «−» перед числом. А именно, отрицательное целое число, записываемое в двоичной системе счисления  , имеет величину:

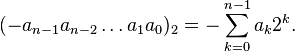
В вычислительной технике широко используется запись отрицательных двоичных чисел в дополнительном коде.

Дробные числа[править | править исходный текст]

Дробное число, записываемое в двоичной системе счисления как  , имеет величину:

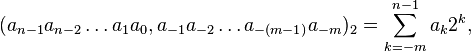
где:

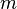•  — число цифр дробной части числа,

•  — цифры из множества  .

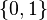Сложение, вычитание и умножение двоичных чисел[править | править исходный текст]

Таблица сложения

+	0	1
0	0	1
1	1	10(перенос в старший разряд)

Таблица вычитания

-	0	1
0	0	1
1	(заём из старшего разряда) 1	0

Пример сложения «столбиком» (14₁₀ + 5₁₀ = 19₁₀ или 1110₂ + 101₂ = 10011₂):

+		1	1	1	0
			1	0	1
	1	0	0	1	1

Таблица умножения

×	0	1
0	0	0
1	0	1

Пример умножения «столбиком» (14₁₀ * 5₁₀ = 70₁₀ или 1110₂ * 101₂ = 1000110₂):

×				1	1	1	0
					1	0	1
+				1	1	1	0
		1	1	1	0
	1	0	0	0	1	1	0