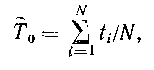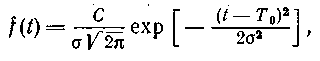Определение множества Парето Непрерывный случай.

Е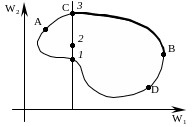 сли множество точек, в котором небольшое улучшение влечёт за собой небольшое изменение . Пусть есть два показателя .

Сравним безусловную пару вариантов: третий безусловно лучше второго и первого. На дуге находятся лучшие точки при , а на дуге лучшие точки при . Поэтому точками множества Парето будут являться точки находящиеся на дуге .

Порядок выполнения работы.

В качестве исходного материала используется таблица параметров качества и цены заданной предметной области (Лабораторная работа №3)

1. Нормирование показателей качества Xi. Нормирование производиться для устранения влияния размерности и диапазона изменения показателя на целевую функцию качества. После нормирования все показатели качества имеют диапазон изменения от 0 до 1. Значение 0 соответствует худшему из возможных значений, а 1- лучшему.

Нормирование производиться по формулам.

1 Если качество возрастает с увеличением значения параметра	2 Если качество уменьшается с увеличением значения параметра
Xni = (Xi - Xmin) / (Xmax - Xmin)	Xni = (Xmax - Xi) / (Xmax - Xmin)
Где Xni-нормированное значение Xi показателя качества, Xmax, Xmin максимальное и минимальное значение Xi показателя качества

2. Выбираются значения персональных оценок весовых коэффициентов. Весовые оценки выбираются в соответствии с приоритетами лица принимающего решение.

№	Сумма оценок	Число передач	Высота подъема руля	Диаметр колес	Вес, кг	Остаточная стоимость через 2-3 года
	1	0,5	0,2	0,1	0,1	0,1

3. Определяем значение целевой функции качества F

для каждого из возможных вариантов выбора, где ai – весовые коэффициенты, Xni - нормированные значения параметров качества.

4. Составляем множество Парето, т.е. выбираем варианты, где с увеличение цены возрастает и качество. Например, для велосипедов

Модель	Функция качества	Цена, RR
Schwinn Sierra 7	0,266757	10977
KHS	0,429306	13566
Trek Atwood	0,539419	15140
Marin Muirwoods	0,624268	16500
Schwinn Sportera	0,737602	18132
Orbea Anayet	0,83402	35420

Содержание отчета

1.Таблица нормированных значений параметров качества.

2. График распределения вариантов выбора в координатах цена-качество

3.Парето оптимальное множество.

Контрольные вопросы.

1. Дать определение понятию эффективное множество Парето

2. Как формировалась функция качества изделия.

Работа №7 Оценка вероятности безотказной работы оборудования

Цель Разработка программного обеспечения для оценки надежности имеющегося оборудования и принятия решения о его замене.

Теоретический материал

Принцип практической уверенности

В теории вероятностей и математической статистике чрезвычайно важную роль играют так называемые практически невозможные и практически достоверные события.

Практически невозможным называется такое событие, вероятность которого очень близка к нулю (например, 0,1; 0,05; 0,001 и т. д.).

Практически достоверным называется такое событие, вероятность которого очень близка к единице (например, 0,9; 0,95; 0,99; 0,999 и т. д.).

Очевидно, что если событие А практически невозможное, то его противоположное событие А будет практически достоверным.

Если вероятность одного случайного события 0,4, то предсказать с уверенностью результат опыта при однократном проведении невозможно, но если вероятность события 0,99 или 0,01 это уже становится возможным. В данном случае используем так называемый принцип практической уверенности, сформулировать который можно так: если вероятность появления данного события А очень мала (очень велика), можно быть практически уверенным в том, что при однократном проведении соответствующего опыта событие А не появится (появится). Конечно в таком случае имеется известный риск: событие, которое считаем практически невозможным, может наступить и привести к очень неблагоприятным последствиям. Вероятность α, при которой данное событие можно считать практически невозможным, называется уровнем значимости, а вероятность γ, при которой событие можно считать практически достоверным, называется доверительной вероятностью.

Вопрос о том, насколько мала (велика) должна быть вероятность появления данного события А, чтобы оно считалось практически невозможным (достоверным), выходит за рамки математической теории и в любом отдельном случае решается в соответствии с конкретными условиями и прежде всего со степенью риска, который возникает при появлении (непоявлении) данного невозможного (достоверного) события.

Например, если вероятность «поломки «мышки» в течение одной рабочей смены» равна 0,1. то можно это событие считать невозможным, т. е. пренебречь его появлением и начать работу. Риск в этом случае главным образом связан с уменьшением производительности. Если же вероятность отказа в системе жесткого диска в банке равна 0,1, то совершенно недопустимо считать это событие практически невозможным. В данном случае риск намного больше. Еще больший риск имеется, если принять за практически невозможное событие «отказ бортового компьютера самолета», даже если его вероятность равна 0,001.

Чем больше риск при появлении пренебрегаемого события, тем при меньшей вероятности а нужно считать данное событие практически невозможным. Однако слишком малые численные значения а не всегда оправданы, так как они связаны с удорожанием

При решении технических задач общего характера, где последствия наступления практически невозможных событий не связаны с большими авариями и тяжелыми потерями, принимается а = 0,1; 0,05 и 0,01 (аналогично у = 0,9; 0,95 и 0,99).

Способы математического описания характеристик надежности

Безотказность объектов можно оценивать следующими основными показателями: средним временем безотказной работы (наработкой на отказ); вероятностью безотказной работы Р (t); интенсивностью отказов λ (t); параметром потока отказов Ω (t).

Среднее время безотказной работы невосстанавливаемых объектов (наработку на отказ) по данным испытаний их на надежность определяют по формуле

где ti — время исправной работы i-го объекта; N — общее число испытуемых объектов.

Для расчета Т₀ необходимо знать продолжительность исправной работы всех испытуемых объектов.

Наработка до момента отказа t является случайной величиной. Закон ее распределения определяется плотностью вероятности f(t). В тех случаях, когда объекты изготовляют в условиях установившегося производства, а отказы возникают в связи с постепенным изменением параметров при изнашивании и старении, время безотказной работы объектов изменяется по нормальному закону.

Плотность распределения вероятности времени безотказной работы объекта при нормальном распределении описывается уравнением

где С — нормирующий множитель; σ — среднее квадратичное отклонение.

Таким образом, нормальный закон характеризуется двумя параметрами: Т₀ и σ. Ввиду ограниченного числа испытаний по полученным данным можно найти лишь статистические оценки этих характеристик и затем с заданной вероятностью α найти доверительные границы, внутри которых должны находиться Т₀ и σ .

При испытаниях фиксируется время наступления отказа: каждого из N объектов, за которыми установлено наблюдение.

В этом

Доверительные границы Т₀ для нормального закона распределения находят из выражений:

где Тн — нижняя доверительная граница; Тв — верхняя доверительная граница; ε — мера точности, которую определяют из выражения

Значения коэффициента tα даны в таблице

Число опытов	Уровень надежности
	0,8	0,9	0,95	0,98	0,99	0,909
2	3,08	6,31	12,71	31,8	63,7	636,6
3	1,886	2,92	4,3	6,96	9,92	31,6
4	1,638	2,35	3,18	4,54	5,84	12,94
5	1,533	2,13	2,77	3,75	4,6	8,61
6	1,476	2,02	2,57	3,36	4,03	8,86
7	1,44	1,943	2,45	3,14	4,71	5,96
8	1,415	1,895	2,36	3	3,5	5,4
9	1,397	1,86	2,31	2,9	3,36	5,04
10	1,383	1,833	2,26	2,82	3,25	4,78
11	1,372	1,812	2,23	2,76	3,17	4,59
12	1,363	1,796	2,2	2,72	3,11	4,49
13	1,356	1,782	2,18	2,68	3,06	4,32
14	1,35	1,771	2,16	2,65	3,01	4,22
15	1,345	1,761	2,14	2,62	2,98	4,14
16	1,341	1,753	2,13	2,6	2,95	4,'07
17	1,337	1,746	2,12	2,58	2,92	4,02
18	1,333	1,74	2,11	2,57	2,9	3,96
19	1,33	1,734	2,1	2,55	2,88	3,92
20	1,328	1,729	2,09	2,54	2,86	3,88
21	1,325	1,725	2,09	2,53	2,84	3,85
22	1,323	1,721	2,08	2,52	2,83	3,82
23	1,321	1,717	2,07	2,51	2,82	3,79
24	1,319	1,714	2,07	2,5	2,81	3,77
25	1,318	1,711	2,06	2,49	2,8	3,74
26	1,316	1,708	2,06	2,48	2,79	3,72
27	1,315	1,076	2,06	2,48	2,78	3,71
28	1,314	1,703	2,05	2,47	2,77	3,69
29	1,313	1,701	2,05	2,47	2,76	3,67
30	1,311	1,699	2,04	2,46	2,76	3,66
31	1,31	1,697	2,04	2,46	2,75	3,65
41	1,303	1,684	2,02	2,42	2,7	3,55
61	1,296	1,671	2	2,39	2,66	3,46
121	1,289	1,658	1,98	2,36	2,62	3,37

Вероятность безотказной работы изделий при нормальном законе распределения

P(t)= 1 – Ф(t).

Гарантированную долговечность определяют по уравнению

где u_α — квантиль нормального распределения, отвечающий заданному уровню вероятности. Для нормального закона приведены в таблице

Значения квантиля при уровне надежности a.

α	0,9	0,95	0,99	0,999
uα	1,282	1,645	2,326	3,090

Практическое задание.

Используя индивидуальную базу данных имеющегося оборудования и характеристики закона распределения времени безотказной работы оценить его состояние. Пример реализован на листе «LR5» файла MISPR_Т2.xls.

Порядок выполнения работы

1. Разработать программу для определения:

1.1 доверительных границ;

1.2 вероятности безотказной работы и гарантированную долговечность. табличные данные u_α — квантиль установить в зависимости от категории отдела 1) 0,9, 2) 0,95и 3) 0,99.

1.3 заключения о необходимости замены оборудования в виде списка, отсортированного по мере уменьшения вероятности отказа.

2. Определить вероятность отказа для всех видов оборудования и сравнить ее с гарантированной долговечностью.

3. Составить отчет

3.1 Содержание отчета

3.1.1. Представить блок схему программы

3.1.2. Представить таблицу с оценкой вероятности отказа для всех видов оборудования и рекомендаций о ее замене.

4. Ответить на контрольные вопросы

4.1 Записать формулу определения вероятности попадания случайной величины X в данный интервал [х1, х2] при нормальном законе распределения.

4.2 Записать уравнение плотность распределения вероятности времени безотказной работы объекта при нормальном распределении.

4.3 Дать определение гарантированной долговечности.

4.4 Дать определение вероятности безотказной работы.