Работа № 5 Законы распределения случайной величины

Цель Разработка программного обеспечения для определения статистических законов распределения характеристик случайной величины

Теоретический материал

Любая случайная величина полностью определяется законом распределения, который имеет две формы.

Для дискретных случайных величин — это ряд распределения и функция распределения, а для непрерывных — функция распределения и плотность распределения.

Ряд распределения содержит все возможные значения дискретной случайной величины и соответствующие им вероятности.

Функция распределения F(х) выражает вероятность Р того, что случайная величина X принимает значение меньшее данного действительного числа х, т. е.

и имеет следующие свойства:

1) численные значения F (х) принадлежат интервалу [0, 1 ]:

2) функция F(х) неубывающая, т. е. если x2 > х1 то F(х2) > F(x1)>;

3) если возможные значения случайной величины X принадлежат интервалу [а, b], то F(х) = 0 при х <= а и F(х) = 1 при х >= b.

Первое свойство связано с самим определением функции распределения как вероятности.

Второе свойство доказывается, если используются несовместимые события: случайная величина X принимает значение меньше х1 и случайная величина X принимает значение больше или равное. х1 и меньше х2.

Тогда событие: «случайная величина X принимает значение меньше х2” является суммой двух написанных выше несовместимых событий, поэтому можем записать равенство

или

Видно, что вероятность того, что случайная величина X попадает в интервал (х1, х2), равна приращению функции распределения в этом интервале. Из этого равенства следует также, что вероятность того, что непрерывная случайная величина примет определенное численное значение, равна нулю. В этом. легко, убедиться, если подставить х2= х1, при этом получим

Отсюда

Из Р(X=x1) = 0 не следует, что событие X = х1 невозможно, т. е. что случайная величина X не может принимать численное значение x1, которое является одним из ее возможных численных значений.

Третье свойство функции распределения становится очевидным из-за того, что событие X < x1 <a невозможно, т. е. F(х1) = 0, а событие X < х2 >= b является достоверным (так как возможные значения X меньше х2 ),т. е. F(х2) = 1.

Если возможные значения непрерывной случайной величины X принадлежат интервалу (-∞, +∞), третье свойство принимает вид

Рассмотренные свойства дают возможность получить представление о характере графика функции распределения. Например, из первого свойства следует, что этот график расположен между осью абсцисс (у = 0) и параллельной ей прямой с уравнением у = 1. Для дискретных случайных величин график функции распределения имеет ступенчатый характер, для непрерывных — монотонно неубывающий.

Плотность распределения f(x) — вторая форма закона распределения непрерывных случайных величин является первой производной функции распределения

Поэтому f(х) называется еще дифференциальной функцией. Если известна f(х), то согласно формуле Ньютона—Лейбница

т. е. вероятность попадания непрерывной случайной величины X в интервал (х1, х2) равна значению определенного интеграла от плотности распределения f(х), вычисленному в пределах от х1 до х2. Геометрически это означает, что вероятность попадания X в интервал (х1, х2) равна площади криволинейной трапеции, ограниченной сверху графиком плотности распределения f(х), снизу осью абсцисс х, а с боков вертикальными прямыми х = х1 и х = х2 (рис. 2.1).

	Если подставим то получим

Отсюда вытекает второе название функции F(х)— интегральная функция.

При достаточно малом dх вероятность попадания непрерывной случайной величины X в интервал (х, х + dх) приблизительно равна площади прямоугольника с основанием dх и высотой f(х) (см. рис. 2.1).

Величина f(х) их называется элементарной вероятностью. Так как вероятность — безразмерная величина, то размерность плотности распределения f(х) обратна размерности случайной величины X.

Плотность распределения f(х) имеет следующие свойства:

1) она неотрицательна, т. е. f(х) > 0;

2) несобственный интеграл от f(х) в пределах от -∞до +∞ равен единице, т. е.

Если возможные значения X принадлежат интервалу (а, Ь), то (2.8) принимает вид

Таким образом, видно, что полная площадь, ограниченная графиком f(х) и осью абсцисс, равна единице.

Принято график плотности распределения f(х) называть кривой распределения.

Нормальный закон распределения, известный так же как закон Гаусса, находит широкое применение в различных областях познания. Он играет исключительно важную роль в теории вероятностей, теории ошибок, математической статистике и т. д. Именно для случая нормального распределения разработаны наиболее полно различные статистические методы.

Чрезвычайно широкое приложение нормального закона основывается на центральной предельной теореме. Согласно этой теореме, если имеем n независимых случайных величин Х1, Х2, . . ., Хn с конечными математическими ожиданиями и дисперсиями, то при n -›∞ закон распределения суммы или среднеарифметического значения данных случайных величин неограниченно стремится к нормальному, независимо от их закона распределения, достаточно только, чтобы между случайными величинами Х1, Х2, . . ., Хn не было доминирующих относительно влияния на сумму.

На практике считается, что распределение суммы 10—20 одинаково распределенных случайных величин достаточно близко к нормальному закону. В частном случае, когда случайные величины распределены по закону равной вероятности в интервале [0, 1], даже при n = 6 получается приемлемое приближение к нормальному закону.

Главной особенностью нормального закона является то, что это предельный закон, к которому стремятся остальные законы распределения при определенных условиях. Нормальный закон можно использовать и тогда, когда известен истинный закон распределения, но приближенное представление через нормальный закон удобнее для работы.

Плотность распределения при нормальном законе задают следующей формулой:

где а и Ь — действительные постоянные, принимающие в каждом случае конкретные значения.

Видно, что распределенная по нормальному закону случайная величина X может изменяться в интервале (-∞, +∞). Встречающиеся на практике случайные величины обычно изменяются в каких-либо конечных интервалах. Это обстоятельство не мешает использованию нормального закона для описания таких случайных величин.

Эта возможность базируется на том, что в конечный интервал длиной 6σ[X] и серединой, совпадающей с m₁ [X], практически попадают все возможные значения распределенной по нормальному закону случайной величины X. В этом мы убедимся дальше.

Постоянные а и b плотности распределения называются параметрами нормального закона и однозначно определяют его.

График плотности распределения нормального закона имеет вид, показанный на рис. 2.3.

Он симметричен относительно вертикали, отстоящей от начала координат на расстоянии а, имеет максимум в точке х = а, который равен 1/b√(2), и перегибы в точках х = а — Ь и х = а + Ь. Математическое ожидание m₁[X ] распределенной по нормальному закону случайной величины X можно определить по формуле:

т. е. параметр а нормального закона равен математическому ожиданию m₁[X ] случайной величины X. Аналогично получается

т. е. параметр b нормального закона равен среднему квадратичному отклонению σ[X ] соответствующей случайной величины X.

То, что данная случайная величина X распределена по нормальному закону с математическим ожиданием m₁[X ] и средним квадратичным отклонением σ[X] = Ь, можно записать так: X ~ N (а, Ь).

На рис. 2.4 показана кривая распределения нормального закона для различных значений а и Ь. Изменение параметра а приводит только к перемещению кривой распределения, не изменяя ее формы, поэтому данный параметр называется также центром распределения.

При изменении параметра Ь форма кривой распределения также не изменяется, но изменяется ее масштаб по обеим координатным осям . С уменьшением значения этого параметра увеличивается доля значений случайной величины X, сосредоточенных в окрестности точки х = а, т. е. в окрестности m₁[X ].

Одной из задач, часто решаемых с помощью этого закона распределения, является задача определения вероятности попадания случайной величины X в данный интервал [х1, х2]. “та вероятность

Определенный интеграл в правой части нельзя вычислить точно, так как соответствующий неопределенный интеграл не выражается конечным числом элементарных функций. Для приближенного вычисления интеграла приходится численно интегрировать функцию f(x) или воспользоваться стандартной функцией листа Excel НОРМРАСП(x;среднее;стандартное_откл;интегральная).

Параметры функции: x — значение, для которого строится распределение; Среднее— оценка значения m₁[X ]=а.; Стандартное_откл— оценка значения σ[X] = Ь; Интегральная— логическое значение, определяющее форму функции. Если интегральная имеет значение ИСТИНА, то функция НОРМРАСП возвращает интегральную функцию распределения; если это аргумент имеет значение ЛОЖЬ, то возвращается функция плотности распределения.

Для самостоятельного вычисления значения функции F(x) необходимо проинтегрировать функцию f(x) с помощью правила трапеций в интервале от x1=a-3b до x2=x.

Практическое задание.

Используя индивидуальную базу данных определить характеристики закона нормального распределения.

Порядок выполнения работы

1. Разработать программу для определения

1.1 среднего значения параметров качества;

1.2 среднего квадратичного отклонения параметров качества;

1.3 плотности распределения параметров качества ;

1.4 численного интегрирования функции f.

3. Составить отчет

3.1 Содержание отчета

3.1.1. Представить блок схему программы

3.1.2. Представить графики функции распределения и плотности параметров качества. (Пример Графики распределения веса велосипедов)

4. Ответить на контрольные вопросы

4.1. Дать определение функции распределения и указать три ее основных свойств.

4.2 Дать определение плотности распределения.

4.3. Записать формулу Ньютона—Лейбница и дать ее геометрическое толкование

4.4 Записать формулу плотности экспоненциального распределения и указать смысл постоянной λ

4.5 Записать формулу плотности при нормальном законе распределения и пояснить смысл, входящих в нее величин.

4.6 Дать определение понятию «квантили случайной величины»

4.7 Показать как изменяется кривая распределения нормального закона для различных значений а и b.

Лабораторная работа № 6 Задача принятия решения на основе многокритериальной оптимизации.

Цель Изучения выбора вариантов с использованием множества Парето.

Теоретический материал.

В задаче принятия решения назовем пару (Ω, Ρ),

где Ω – множество вариантов (альтернатив),

Р – принцип оптимальности.

Решением задачи является множество , получающееся в соответствии с принципом оптимальности Р. Отсутствие хотя бы одного из элементов (Ω, Ρ) лишает задачу смысла.

Математическим выражением принципа оптимальности Р служит функция выбора С_р, которая со всеми подмножествами его часть С_р(х). Таким образом, решением исходной задачи является С_р(Ω).

Задача принятия решения различается в зависимости от информации о множестве Ω и принципе оптимальности Р:

1. Общая задача принятия решения: Ω, Р – неизвестны, необходимо 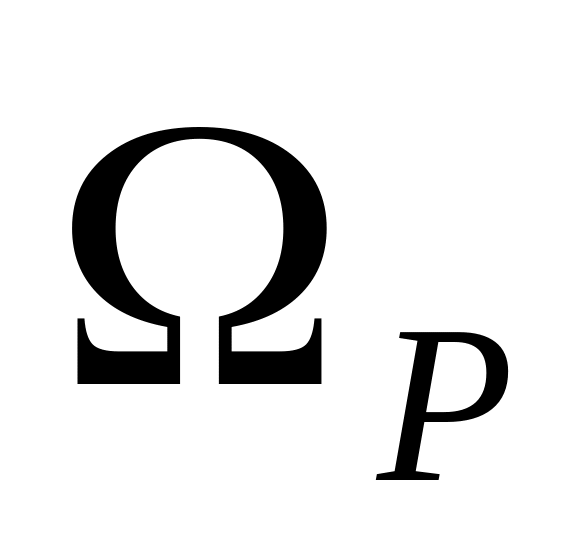получить в процессе самого решения.

2. Задача с известными Ω называется задачей выбора.

3. Задача, в которой Ω, Ρ – известны называется общей задачей оптимальности.

Во многих задачах при моделировании критерия приходится назначать много критериев. Оказывается, что изменение одного критерия, несёт за собой изменение другого критерия. Существует принципиальная трудность в оценке двух или более вариантов. Особенно если их оценивать безусловно.

Векторная оптимизация:

1. Безусловная оптимизация, когда пытаются определить безусловно лучшее решение, но после этапа безусловной оптимизации можно отсеять заведомо невыгодные решения, т. е. безусловно сравнённые и худшие, поэтому несравнимые, но и не плохие остаются, и мы получаем эффективное множество – множество Парето.

2. Для нахождения наилучшего решения приходится вводить некоторые условия, например, предпочтения или приходится выбирать из всех важных критериев, какой из них самый ценный.