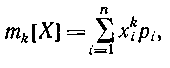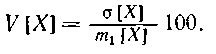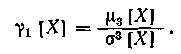Работа №4 Числовые характеристики случайных величин

Цель Разработка программного обеспечения для определения статистических характеристик случайной величины.

Теоретический материал

Часто при изучении явления или процесса не нужно знать подробно случайные величины, которые его описывают, т. е. знать законы распределения этих величин, а вполне достаточно знать некоторые их особые численные значения и характеристики. Такими характеристиками являются моменты, квантили и числовые характеристики. При этом одни числовые характеристики полностью совпадают с некоторыми моментами, а другие являются их функциями.

Понятие «момент» широко используется в механике для описания распределения масс и площадей (статические моменты, моменты инерции и т. д.). Аналогичным образом это понятие используют в теории вероятностей для описания распределения значений случайной величины. При этом в теории вероятностей чаще всего используют начальные и центральные моменты и реже абсолютные. Для всех видов моментов существует так называемый порядок соответствующего момента.

Начальный момент k-го порядка случайной величины X обозначается m_k [X]. Для дискретных случайных величин его определяют по формуле

где n—число возможных значений X; x_i;— i-е значение X; р_i — вероятность, с которой X принимает численное значение x_i.

В теории и практике чаще всего используют первый начальный момент m₁[X ]. Если из X вычесть m₁ [X ], то получим так называемую центрированную случайную величину

Начальные моменты центрированной случайной величины X называют центральными моментами нецентрированной случайной величины X, обозначают μ_k[X] и для дискретных случайных величин

Из центральных моментов чаще всего используют второй μ₂ [X], который совпадает с так называемой дисперсией σ²[X] случайной величины X. Первый центральный момент всех случайных величин равен нулю, т. е. μ₁ [X]=0.

Числовые характеристики случайной величины делятся на следующие группы:

1) определяющие положение случайной величины;

2) определяющие рассеивание случайной величины;

3) связанные с симметрией и степенью заострения кривой распределения случайной величины.

К первой группе характеристик относятся: среднее значение, мода и медиана. Из этих характеристик самую важную роль в теории вероятностей играет среднее значение m₁[X], которое называют также математическим ожиданием. Математическое ожидание данной случайной величины совпадает с ее первым начальным моментом, который вычисляют по формуле (2.10) или (2.11), если положить k = 1.

Математическое ожидание является центром, около которого группируются в той или другой степени возможные значения данной случайной величины.

Модой М случайной величины X называют ее численное значение, которому соответствует самая большая вероятность для дискретных случайных величин и максимум плотности распределения f(x) — для непрерывных.

Если плотность распределения f(x) имеет только одну моду (один максимум), распределение называют одномодальным. В дальнейшем будем рассматривать только одномодальные распределения.

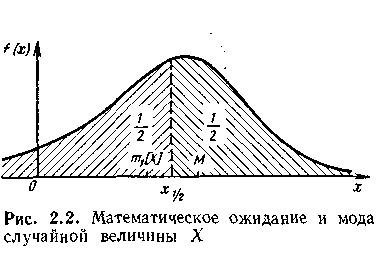
Медианой называют численное значение x_1/2 случайной величины, для которого выполнено условие

Для непрерывных случайных величин медиана равна абсциссе точки, ордината которой делит площадь под кривой распределения на две равные части.

Если для дискретных случайных величин нельзя найти численное значение, которое удовлетворяет условию, то определяют такие соседние значения х_k, и x_k+1, для которых выполняются неравенства

Тогда медианой будет среднее арифметическое этих двух соседних значений:

Если распределение симметрично относительно m₁[X], то медиана и математическое ожидание совпадают. Если при этом распределение одномодальное и x_1/2, совпадает с М и m₁[X] то мы имеем дело с широко используемым в теории и практике нормальным распределением.

Ко второй группе числовых характеристик случайной величины относятся: размах, дисперсия, среднее квадратичное отклонение и коэффициент вариации. Реже используется так называемое среднее арифметическое отклонение.

Размах R равен разности между самым большим и самым малым значениями X, т. е.

Дисперсия σ²[X] данной случайной величины равна математическому ожиданию квадрата отклонения случайной величины от ее математического ожидания:

Дисперсия является основной характеристикой рассеивания Данной случайной величины относительно математического ожидания. Само название «дисперсия» означает «рассеивание». Из формулы (2.16) видно, что дисперсия совпадает со вторым центральным моментом М₂ [X].

Для дискретных случайных величин

Дисперсию можно представить через первый и второй начальные моменты:

Так как дисперсия представляет собой сумму положительных слагаемых, которые являются квадратами отклонений случайной величины от математического ожидания, то малая дисперсия будет показывать, что эти слагаемые.(отклонения) малы и, следовательно, мало рассеивание. Наоборот, большая дисперсия показывает, что по крайней мере одно из отклонений велико и, следовательно, рассеивание большое. Это показывает, что, действительно, дисперсия может служить мерой степени рассеивания. Однако при использовании дисперсии имеется одно неудобство — ее размерность равна квадрату размерности изучаемой случайной величины, поэтому более удобной характеристикой рассеивания считается так называемое среднее квадратичное отклонение σ[X], которое определяют по формуле

При сравнении степени рассеивания двух случайных величин Х1 и Х2 необходимо иметь в виду также их математические ожидания m1[Х1] и m2[Х2]. Если они равны между собой, то сравнение можно проводить по σ² [Х1] и σ² [Х2] или по соответствующим средним квадратичным отклонениям. Если m1[Х1] не равно m2[Х2], то приходится использовать так называемый коэффициент вариации V [X], который определяют по формуле (в %)

Коэффициент вариации является относительной мерой рассеивания. Характеристики рассеивания σ[X] и V [X] являются основными критериями для оценки качества и надежности работы различных технических устройств.

К третьей группе числовых характеристик относятся асимметрия и эксцесс. Значения некоторой случайной величины X могут быть распределены симметрично или асимметрично относительно математического ожидания m₁ [X]. Степень асимметрии (несимметрии) данного распределения характеризуют коэффициентом асимметрии γ₁[X], который вычисляют как отношение третьего центрального момента μ₃ [X] к σ[X], возведенному в третью степень:

Использование μ₃ [X] для определения степени асимметрии основывается на следующем. Как мы уже видели, первый центральный момент μ₁[X] всегда равен нулю. Это делает первый и все четные центральные моменты негодными для характеристики степени асимметрии. Нечетные центральные моменты третьего и более высокого порядков равны нулю только при симметричных распределениях. Так как с увеличением порядка центрального момента возрастает сложность его вычисления, логично при определении степени асимметрии использовать самый простой из них, т. е. третий центральный момент.

При γ₁ > 0 говорим о положительной (левой) асимметрии, а при γ₁ < 0 — об отрицательной (правой) асимметрии.

Эксцесс γ₂ [X] данного распределения характеризует степень его заостренности и вычисляется по формуле

Основой для определения степени заостренности данного распределения является нормальное распределение при одной и той же дисперсии обоих распределений, При нормальном распределении. отношение четвертого центрального момента к σ⁴ [X] равно трем. Таким образом, эксцесс нормального распределения равен нулю.

Из всех рассмотренных до сих пор числовых характеристик самое большое приложение при исследовании и испытании имеют математическое ожидание, дисперсия, среднее квадратичное отклонение и коэффициент вариации. Значительную информацию о распределении случайной величины дают и ее квантили. Квантили задают вероятность попадания случайной величины в интервал. Например α-квантиль х_α определяется из условия

Практическое задание

Разработать программное обеспечение для определения статистических характеристик распределения параметров качества объектов предметной области (лабораторная работа 3).

3. Составить отчет

3.1 Содержание отчета

3.1.1. Представить блок схему программы

3.1.2 Представить значения

- оценки математического ожидания с помощью среднего значения,

- оценки математического ожидания с помощью медианы,

- оценки математического ожидания с помощью моды,

-оценки дисперсии и среднего квадратичного отклонения,

- оценки коэффициента вариации,

- оценки асимметрии и эксцесса.

4. Ответить на контрольные вопросы

4.1. Дать определение дискретной и непрерывной случайной величины и указать способы их задания.

4.2. Дать определение начального момента k-го порядка случайной величины.

4.3 Указать числовые характеристики определяющие положение случайной величины

4.4 Указать числовые характеристики определяющие рассеивание случайной величины

4.5 Указать числовые характеристики связанные с симметрией и степенью заострения кривой распределения случайной величины.

4.6 Дать определение репрезентативной выборке.

4.7 Дать определения несмещенной и состоятельной оценки характеристик случайной величины.

4.8 Сравнить эффективность оценки математического ожидания с помощью среднего значения и медианы.