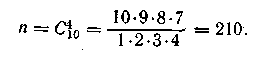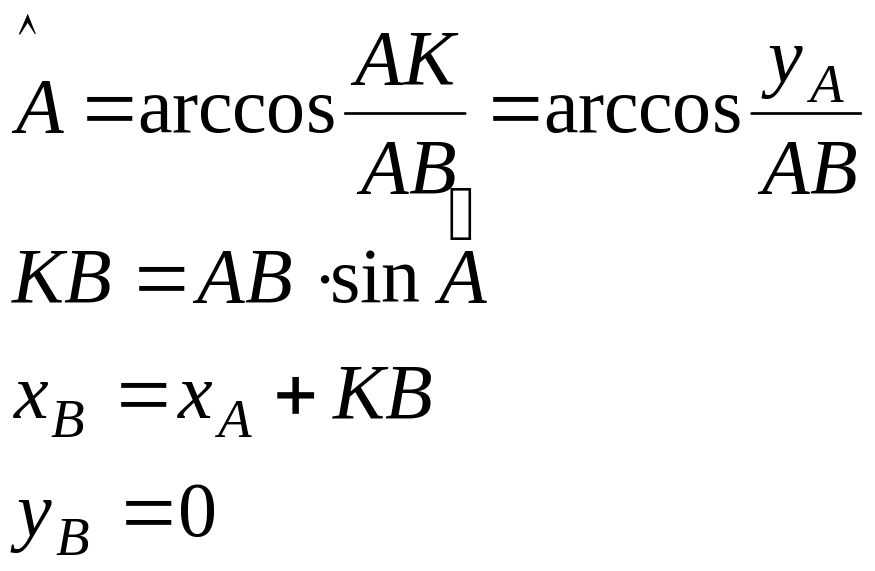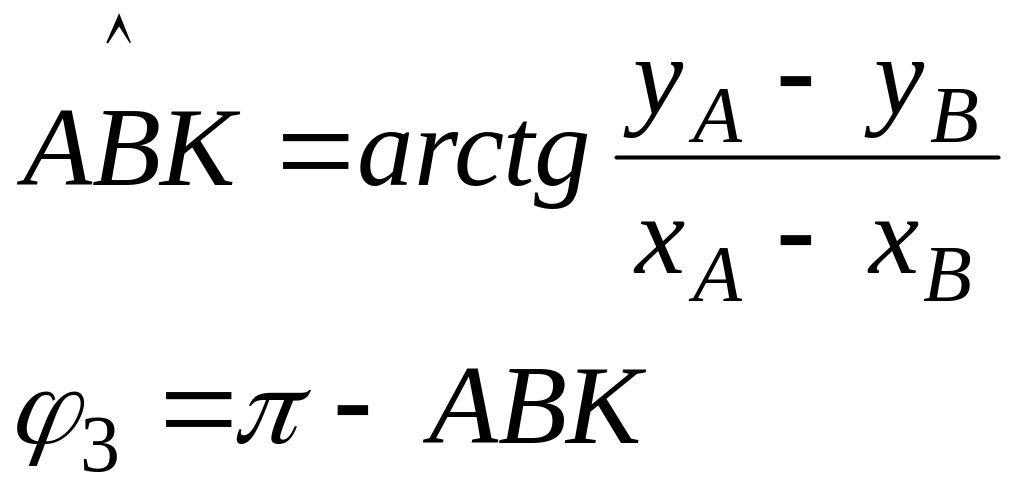Министерство образования Республики Беларусь

Министерство образования и науки Российской Федерации

Учреждение образования

БЕЛОРУССКО-РОССИЙСКИЙ УНИВЕРСИТЕТ

К афедра «Автоматизированные системы управления»

С.К. Крутолевич Н.М. Щербо

ЭКСПЕРТНЫЕ СИСТЕМЫ

Лабораторный практикум

для студентов специальности

"Автоматизированные системы обработки информации"

Могилев 2013

Данный лабораторный практикум содержит 12 лабораторных работ, выполнение которых закрепляет материал, изложенный в электронном конспекте лекций по дисциплине «Экспертные системы» С.К. Крутолевич, Н.М. Щербо, Могилев 2013.

Для выполнения лабораторных работ необходимо получить у преподавателя файл “№варианта”.xls с индивидуальной базой исходных данных.

Лабораторная работа №1 Проведение математического моделирования.

Случайные события. Определение вероятности.

Цель Разработка программного обеспечения для моделирования процесса возникновения случайных событий

Теоретический материал

Теория вероятностей рассматривает не все случайные эксперименты, а только те, которые имеют свойство статистической устойчивости. Прежде чем объяснить это свойство, введем некоторые основные понятия.

Случайный эксперимент определяется совокупностью условий, в которых он проводится, и совокупностью всех возможных результатов. Проведение случайного эксперимента предполагает выполнение определенного комплекса условий. Случайный эксперимент, т. е. проведение опыта и получение соответствующего результата, называют еще испытанием.

Считается, что часть условий, определяющих случайный эксперимент, остается постоянной по объективным и субъективным причинам. Наряду с постоянными условиями на результаты случайного эксперимента оказывает влияние также и ряд объективных факторов, поведение которых не известно или известно частично. Постоянные условия определяют именно то среднее, о котором можно говорить уверенно, то, что устанавливается закономерно в случайных явлениях. Постоянные условия дают возможность повторения случайного эксперимента произвольное число раз, при этом выявляется средняя закономерная тенденция. Переменные факторы (условия) определяют случайное, непредсказуемое в случайном эксперименте. Отсюда, говоря о повторении опыта при одинаковых условиях, нужно иметь в виду, что неизменными остаются условия только первой группы — постоянные.

При обработке некоторой детали на станке можно поддерживать постоянными скорость и глубину резания, подачу, марку материала и т. д. Однако однородность материала, первоначальные размеры заготовки, вибрации станка и т. д. изменяются в определенных не всегда известных нам пределах. Поэтому при подобном опыте возможны различные конечные результаты, которые нельзя предсказать до его проведения. Благодаря постоянным условиям опыта можно определить в среднем, какая часть продукции будет годной, а какая нет. Однако из-за переменных факторов до обработки данной детали нельзя сказать будет она годной или нет.

Любой факт (исход, результат), который может появиться или не появиться при проведении опыта, называется в теории вероятностей случайным событием. Например, в рассмотренном эксперименте возможны следующие исходы: обработанная деталь окажется годной или негодной. Это два случайных события, каждое из которых может наступить или не наступить в результате проведенного опыта. Случайное событие чаще всего обозначают прописными латинскими буквами А, В, С, D и т. д.

В качестве случайного события можно рассматривать работоспособность дискеты, время до отказа вычислительной техники.

Теперь объясним понятие статистическая устойчивость. Это необходимое свойство изучаемых в теории вероятностей случайных экспериментов. Пусть А одно из возможных событий данного случайного эксперимента, этот эксперимент повторен n раз и при этом событие А появилось m раз.

(1.1)

Величина f_A называется относительной частотой появления события А. Если повторить несколько раз серию, состоящую из n одинаковых опытов, то в общем случае величина f_A не будет постоянной. Ее численные значения будут различными также и при разных значениях n. Свойство устойчивости в данном случае состоит в том, что при большом n относительная частота f_A начинает слабо колебаться около некоторого постоянного числа.

При многократном наблюдении за одним или несколькими случайными экспериментами можно заметить, что некоторые события появляются чаще, а другие реже. Это значит, что одни имеют большую возможность появления, а другие меньшую. Например, если многократно подбрасывать две игральные кости и подсчитывать сумму появляющихся очков, то можно заметить, что некоторые суммы, например 6, 7, 8, появляются чаще, а другие, например 2, 3, 11, 12 — реже.

Мерой объективной возможности появления данного случайного события А является его вероятность Р(А). Вероятность появления данного события —• объективная величина, которая существует независимо от экспериментатора. Она определяется полной совокупностью условий, при которых может появиться данное событие. Сказанное здесь математически не объясняет понятия вероятность, так как оно не определяет ее количественно. Исчерпывающей математической формулировки этого понятия все еще не существует. Важное значение для теории и практики имеют приведенные дальше определения этого фундаментального понятия.

В основе классического определения вероятности лежит одно элементарное понятие о равновозможных событиях, которое не подлежит определению. Если в данном случайном эксперименте имеем равновозможные события, то при его многократном повторении можно ожидать, что эти события появятся равное число раз. Типичные примеры равновозможных событий дает подбрасывание игральной кости или монеты.

Если возможные события некоторого случайного эксперимента не могут быть разложены на более простые, то их называют элементарными событиями этого эксперимента. Классическое определение вероятности связано с тем случаем, когда все элементарные события являются равновозможными и при любом опыте появляется только одно из них.

Пусть интересующий нас случайный эксперимент имеет n равновозможных элементарных событий и пусть при появлении m из них наступает и событие А. Тогда можно сказать, что из всех n возможных элементарных событий m благоприятствуют появлению события А. При этом вероятность Р(А) будет равна отношению числа элементарных событий, которые благоприятствуют событию A, к числу всех возможных элементарных событий:

Р(А)=m/n

Это так называемое классическое определение понятия вероятности.

Пример В коробке, состоящей из десяти дискет, есть три негодные. Определить вероятность того, что из четырех случайно отобранных две окажутся негодными.

Решение. Число всех возможных способов выбрать четыре дискеты из десяти равно числу сочетаний С⁴₁₀, образованных из десяти элементов по четыре. Тогда число всех возможных

элементарных событий Сkn=n!/(k!(n-k)!)

Число элементарных событий, которые благоприятствуют событию А, т. е. взятию четырех дискет, две из которых будут негодными, определим так: две негодные дискеты можем взять из трех негодных С²₃ = 3 различными способами. Оставшиеся, две дискеты из четырех должны быть годными, их можно взять из 10 — 3=7 годных дискет С²₇ = 21 различными способами. Этот 21 способ можно сочетать с любым из трех способов взятия двух из трех негодных дискет, т. е. число элементарных событий, которые благоприятствуют событию А, будет m= 3*21 = 63. Тогда искомая вероятность

Практическое задание

Разработать программное обеспечение, для вычислительного эксперимента.

В коробке, состоящей из n дискет, k—негодные. Определить вероятность события А, что из d случайно отобранных b окажутся негодными.

Числовые значения переменных k, d и b в индивидуальном задании.

Реализованный пример на листе “Lr1” файла MISPR_Т1.xls.

В модуле1 данного файла находится программа генерации случайных событий «LR1» и программа определения частоты появления случайного события «Частота».

Порядок выполнения работы:

1. Определить вероятность события А, используя формулы сочетаний.

2. Разработать алгоритм и программу для моделирования данного эксперимента со своими исходными данными.

3. Составить отчет

3.1 Содержание отчета

3.1.1. Представить блок схему программы моделирующей данный эксперимент.

3.1.2. Представить график частоты появления события А от числа опытов.

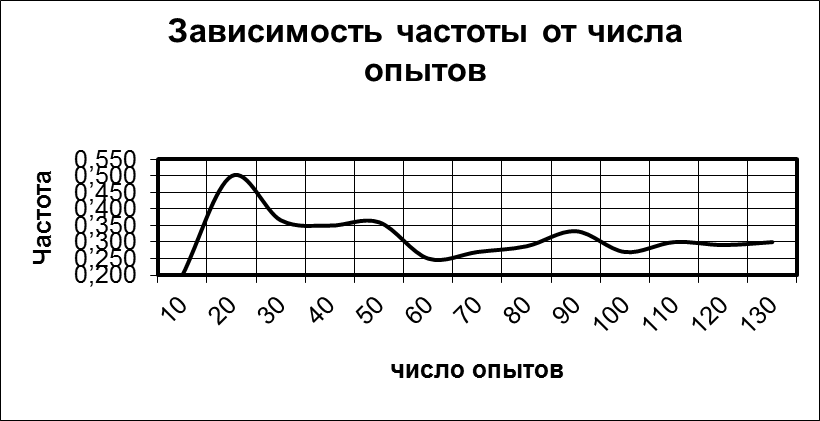
3.1.3. В заключении указать при каком числе опытов выполняется условие, что |f_A-P(A)|<№вар/100

4. Ответить на контрольные вопросы

4.1 Дать определение «относительной частоте появления событий»

4.2 Дать определение «вероятности появления событий»

4.3 Определить вероятность достоверного и невозможного события.

Лабораторная работа №2

Разработка системы автоматизированного проектирования для кинематического анализа и синтеза рычажного механизма.

Цель: Разработка программного обеспечения СППР на основе имитационного моделирования рычажных механизмов.

Теоретический материал.

Целью кинематического анализа является определение координат точек рычажного механизма. Необходимо, задавая положение входного звена ОА через угол определить координаты центров кинематических пар.

Кинематический анализ начинается с входного звена, продолжается с первой присоединенной структурной группы и завершается анализом второй присоединенной структурной группы.

Перед началом геометрического анализа механизмов вспомним некоторые формулы, для решения треугольника.

Прямоугольный треугольник. АВС, С=π/2.

АС=АВ*cos(A), BC=АВ*sin(A), BC=AC*tg(A).

Произвольный треугольник АВС

	A+B+C=
Рис. 1 Решение треугольника

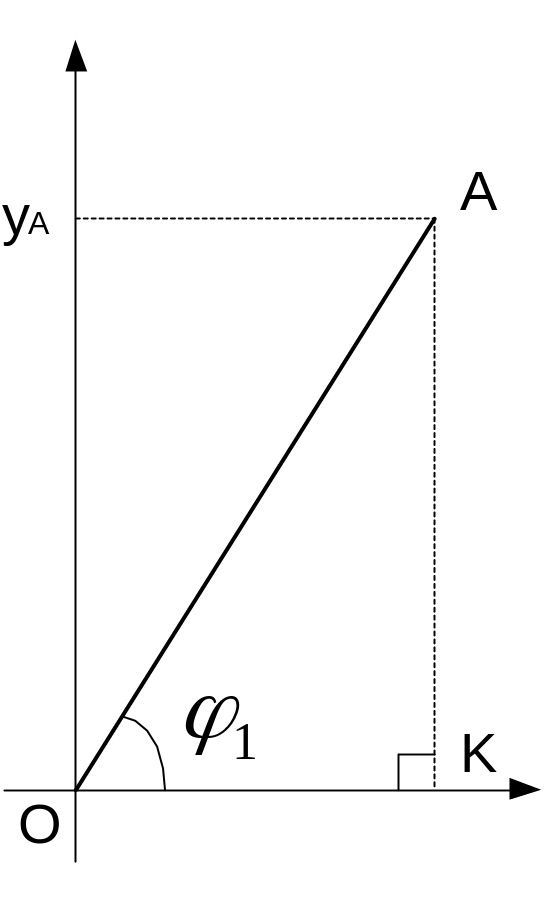
Кинематика входного звена. Свяжем системы координат xoy c точкой о.

	Входное звено ОА образует с системой координат прямоугольный треугольник ОАК. При этом известна длина звена ОА и входной угол . Координаты точки А определяются по формулам. ;
Рис. 2 Решение входного звена.

Структурная группа первого вида. Перед решением структурной группы первого вида должны быть известны координаты внешних точек А и С. Цель решения найти координаты точки В.

	1 Определим расстояние АС 2 Определим угол между осью Х и лучом СА. 3 Определим угол С треугольника АСВ, угол φ3 между осью Х и лучом СВ и координаты точки В
Рис. 3 Решение структурной группы первого вида

Структурная группа второго вида.

Для облегчения вывода удобно совместить одну из осей координат с направляющей.

Известны координаты внешней точки А и положение направляющей, вдоль которой перемещается точка В. Данная направляющая задает одну из координат точки В. Необходимо определить вторую координату точки B.

	В прямоугольном треугольнике АВK определяется угол А. Затем расстояние КВ и координату х точки В. В данном случае Yb=0
Рис. 4 Решение структурной группы второго вида

Структурная группа третьего вида.

В данной группе координаты внешней вращательной кинематической пары А и внутренней поступательной кинематической пары А’ совпадают. Поэтому их отмечают одной буквой. Координаты второй внешней вращательной пары О₁ также заданы. Требуется найти угол между звеном О₁А и координатной осью 0Х.

.

	Из треугольника АВK определяется величина угла АВК. Искомый угол φ3 дополняет АВК по величины π
Рис. 5 Решение структурной группы третьего вида

Структурная группа пятого вида.

В данной группе координаты внешней вращательной кинематической пары А и внутренней поступательной кинематической пары А’ совпадают. Поэтому их отмечают одной буквой. Одна из координат второй внешней поступательной пары С также задана. Требуется найти вторую координату точки С.

	Вторая координата точки С совпадает с координатой точки А. YC=const, XC=XA
Рис. 6 Решение структурной группы пятого вида

Порядок выполнения работы:

1. В соответствии с заданной схемой механизма необходимо составить математическую модель определения координат: центров кинематических пар от угла поворота φ входного звена от оси ОХ.

2. Разработать алгоритм и программу для моделирования данного эксперимента со своими исходными данными. Угол φ изменяется от 0 до 2π. При этом механизм совершает один цикл движения.

Вариант механизма выбирается из приложения 1 в конце лабораторного практикума.

3. Составить отчет

3.1 Содержание отчета

3.1.1. Представить математическую модель моделирующей данный эксперимент.

3.1.2. Представить блок схему программы

3.1.3. Привести распечатки различных положений механизма.

4. Ответить на контрольные вопросы

4.1 Дать определение «кинематическая пара»

4.2 Дать определение «число степеней свободы»