5.9 Построение плана угловых скоростей редуктора

Проводим вертикальный отрезок PS произвольной длины. Через точку Р проводим горизонтальную прямую, а через точку S прямые под углами , , , , к вертикальному отрезку PS, до пересечения с горизонталью. Точки пересечения обозначим 1, 2, Н=4, 5=6, 7 соответственно. Отрезки Р1, Р2, РН=Р4, Р5=Р6, Р7 изображают угловые скорости зубчатых колес 1, 2, 3, 4, 5, 6, 7 и водила Н – , , , , .

Вычисляем масштабный коэффициент плана угловых скоростей:

, (5.18)

Вычисляем угловые скорости звеньев редуктора:

, (5.19)

где – угловая скорость звена N редуктора, ;

– отрезок, который изображает угловую скорость звена N редуктора, мм.

Таблица 5.2 – Угловые скорости звеньев редуктора

	147,35	25	18,65	7,45	3,01
мм	294,7	50	37,3	14,9	6,02

5.10 Определение погрешности кинематического анализа механизма

Вычислим передаточное отношение редуктора с плана угловых скоростей:

(5.20)

Погрешность в определении передаточного отношения редуктора:

(5.21)

Величина относительной погрешности не превышает максимально допустимую.

5.11 Построение картины эвольвентного зацепления

Вычислим геометрические параметры зубчатых колес 6 и 7:

Межосевое расстояние:

(5.22)

Радиусы окружностей вершин:

(5.23)

м

м

Радиусы окружностей впадин:

(5.24)

м

м

Радиусы основных окружностей:

(5.25)

м

м

Высота головки зуба:

м (5.26)

Высота ножки зуба:

(5.27)

м

Высота зуба:

(5.28)

м

Шаг зацепления по начальной окружности:

(5.29)

м

Толщина зуба по начальной окружности:

(5.30)

м

Выберем масштабный коэффициент для построения картины эвольвентного зацепления:

, (5.31)

Вычислим длины отрезков, которые изображают геометрические параметры зубчатых колес 6 и 7:

(5.32)

Таблица 5.3 – Геометрические характеристики эвольвентного зацепления

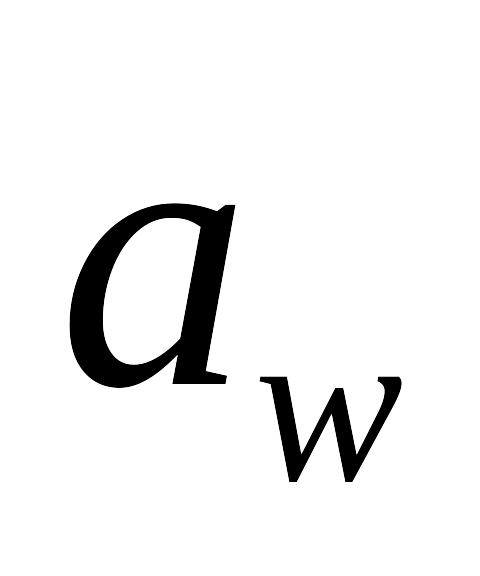
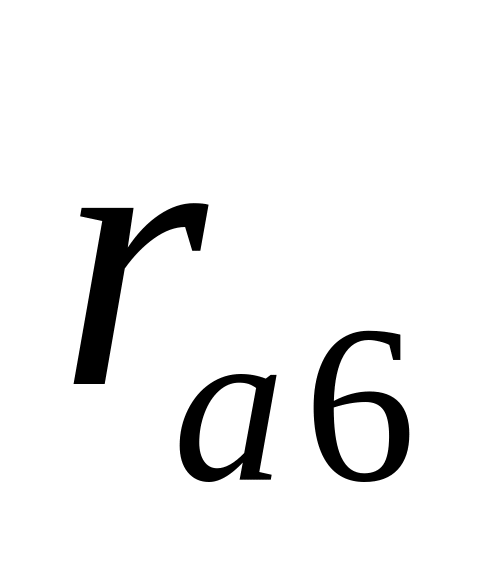
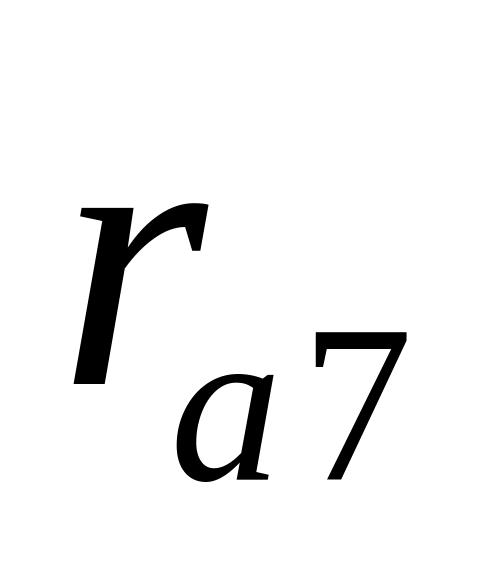
м	0,264	0,084	0,196	0,076	0,188	0,666	0,178
мм	528	168	392	152	376	132	356
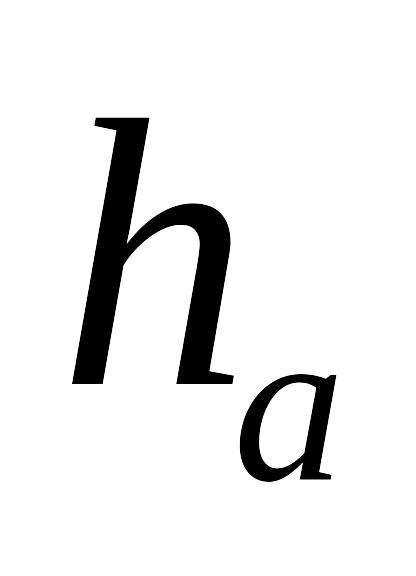
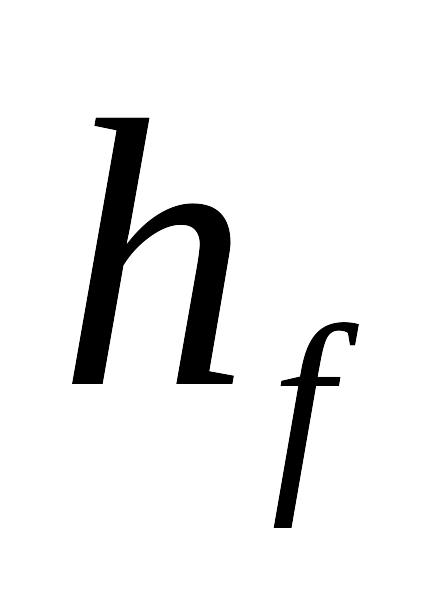
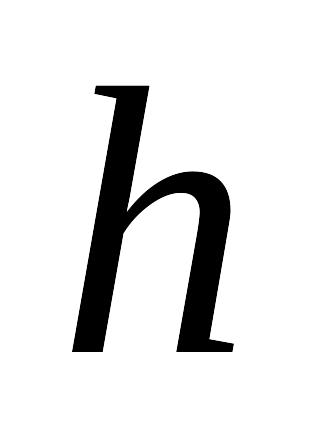
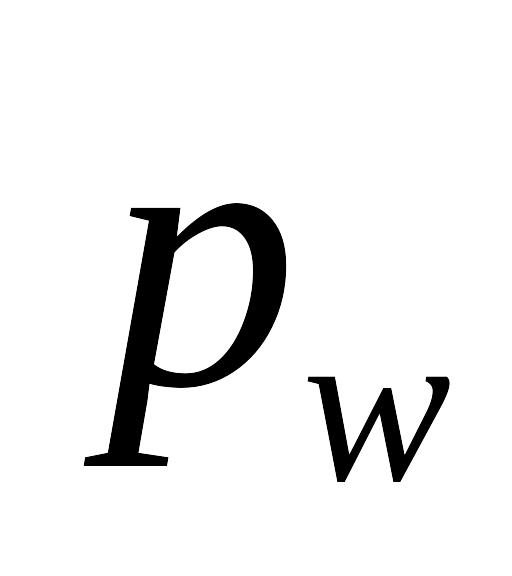
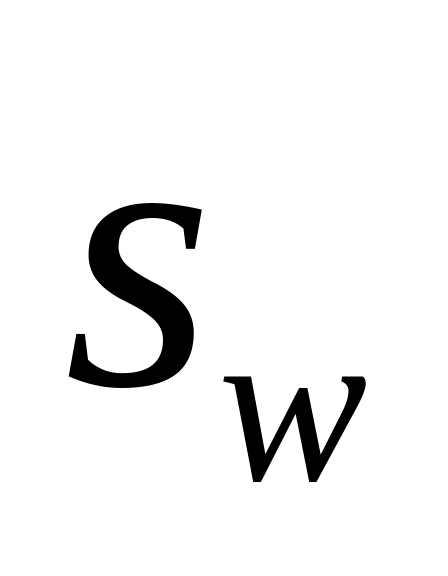
м	0,0714	0,1767	0,008	0,01	0,018	0,0251	0,0126
мм	143	353	16	20	36	50	25

Построим отрезок . Из точек и (оси вращения колес 6 и 7) проведем дуги радиусами , , , , , , , соответственно. Дуги радиусами и должны касаться в одной точке. Обозначим эту точку р – полюс зацепления. Проведем общую касательную к начальным окружностям (перпендикулярно , через полюс р) и общую касательную к основным окружностям (должна пройти через полюс р). Угол между этими двумя касательными должен быть равным углу зацепления . Точки касания касательной к основным окружностям обозначаем и , отрезок – теоретическая линия зацепления. Точки пересечения касательной к основной окружности с окружностями выступов и , отрезок – активная часть теоретической линии зацепления.

Построим эвольвентный профиль зуба колеса 6. Для этого поделим отрезок на 4 равные части и отложим последовательно 4 отрезка длиной по дуге основной окружности колеса 6 от в направлении полюса р. Получим точки 1, 2, 3, 4. Проведем через эти точки касательные к основной окружности (перпендикуляры к ). На этих касательных (образующих эвольвенты) откладываем отрезки: от точки – отрезок , от точки 1 – отрезок , от точки 2 – отрезок , от точки 3 – отрезок , в точке 4 – начало эвольвенты. С другой стороны от точки на основной окружности откладываем отрезки, которые равняются – получаем точки 5, 6,…. Через эти точки проводим касательные к основной окружности и на них откладываем: от точки 5 – отрезок , от точки 6 – , …. Соединив полученные точки на образующих, получаем эвольвенту.

Аналогично выполняем построение для 7-го колеса.

Эвольвентный профиль зуба колеса должен начинаться на окружности впадин, а заканчиваться на окружности вершин зубьев. Поэтому в случае, когда лишнюю часть эвольвенты (между и ) не используем, а в случае, когда , достраиваем часть профиля зуба по радиусу от точки начала эвольвенты на основной окружности. Лишние части эвольвенты, которые выходят за окружность вершин, не используем.

В результате этих построений получили на одной стороне зубья колес 6 и 7. Другую сторону профиля получаем путем отображения полученной эвольвенты профиля относительно осей симметрии зубьев. Учитываем, что толщина зуба и ширина впадин на начальной окружности одинаковые и равняются . От полюса р на начальных окружностях откладываем отрезки длиной , проводим через соответствующие точки (полученные на начальных окружностях) ось симметрии зубьев и выполняем симметричное отображение эвольвент. Для каждого колеса построим по 3 зуба (т.е. зубья, которые касаются в полюсе р, будут средними с трех).

Через точки и (первая, и последняя точка контакта зубьев колес 6 и 7) проводим пунктирно эвольвентные профили, которые соответствуют построенным ранее (тем, что проходят через полюс р). Точки пересечения этих пунктирных профилей с начальными окружностями колес обозначаем соответственно , , , . Дуги и – дуги зацепления. Снесем точки , на эвольвентные профили, проходящие через полюс р (радиусами , – получаем точки и на профилях). Точки этих профилей, которые лежат, на окружностях выступов обозначаем и . Части профилей зубьев , – рабочие участки профилей зубьев.