3. Расчет переходных процессов при единичном ступенчатом воздействии

Полное представление о качестве переходного процесса системы автоматического управления дает переходная характеристика h(t), т.е. график переходного процесса при единичном ступенчатом воздействии и нулевых начальных условиях.

Метод, основанный на использовании вещественной частотной харак­теристики замкнутой системы, - один из самых распространенных методов построения переходной характеристики.

Этот метод устанавливает зависимость переходной характеристики h(t) от параметров вещественной частотной характеристики P_з(ω) замкнутой системы по возмущению (или по заданию). Эта зависимость имеет вид

(66)

Характеристику P_з(ω) можно получить на основе соответствующей АФЧХ W_з(jω), получаемой из передаточной функции замкнутой системы после подстановки в нее выражения p=jω и выделения вещественной Pз(ω) и мнимой Qз(ω). (ufl частей согласно выражению

W_з(jω)= P_з(ω)+j Q_з(ω) .

Характеристика P_з(ω) строится по общей методике построения частот­ных характеристик, рассмотренной ранее, в диапазоне так назы­ваемых существенных частот.

Существенной частотой ω_c называют такую частоту, при которой орди­ната P_з(ωc)≤0.1 P_з(0) и в дальнейшем ординаты P_з(ω) не превышают значения P_з(ωc) (P_з(0) - значения ординаты P_з(ω) при ω=0 ).

Порядок построения кривой переходного процесса

1. Строят вещественную частотную характеристику замкнутой систе­мы по возмущению P_зf(ω)или по заданию P_зg(ω)

2. Заменяют характеристики P_зf(ω)или P_зg(ω) рядом эквива­лентных фи­гур – трапеций и треугольников. При этом необходимо выпол­нить сле­дующие условия:

1) основания трапеции или треугольника должны быть параллельны оси частот;

2) левая боковая сторона трапеции или треугольника должна совпа­дать с осью координат;

3) правая боковая сторона трапеции или треугольника должна воз­можно более точно совпадать с кривой P_з(ω) ;

4) алгебраическая сумма высот трапеций и треугольников должна быть равна P_з(0) т.е.

∑H_i=P_з(0) ; (67)

5) алгебраическая сумма площадей фигур должна быть равна пло­щади, ограниченной вещественной частотной характеристикой.

На рис. 10 показан пример замены характеристики P_з(ω) эквива­лент­ными фигурами. Вещественная частотная характеристика заменена тремя фигурами: трапециями №I и №2 и треугольником №3. Алгебраи­ческая сумма площадей S соответствующих фигур приближенно равна площади, ограничиваемой кривой P_з(ω) .

3. Определяют основные параметры эквивалентных фигур: полосу (интервал) равномерного пропускания частот ω_α (для фигур №1 и №3 они равны соответственно ωn и ωε ), интервал пропускания частот ω₀ (соответственно ω_А и ω_С), высоту трапеции H₁=b+c, H₃=-c.

Трапеции характеризуются также наклоном стороны трапеции, для фи­гур №1 и №3

(68)

Треугольник характеризуется высотой и полосой пропускания час­тот, так как для него X=0 (поскольку полоса равномерного пропуска­ния час­тот отсутствует). Для фигуры №2 высота H2=d , полоса про­пускания час­тот ω₀₂=ω_n

4. Составляем расчетную таблицу:

Трапеция №1 H1=b+c					Треугольник №2 H2=d					Трапеция №3 H3= -c
ω01=ωd; x1=ωH/ωd				ω02=ωH; x2=0					ω03=ωc; x3=ωE/ωc
1	2	3	4		5	6	7	8		9	10	11	12
Τ	h	t	x1		τ	h	t	x2		τ	h	t	x3

Значения  и h (графы 1, 2, 5, б, 9, 10) для рассчитанного наклона x берут из таблиц h-функций [8;9].

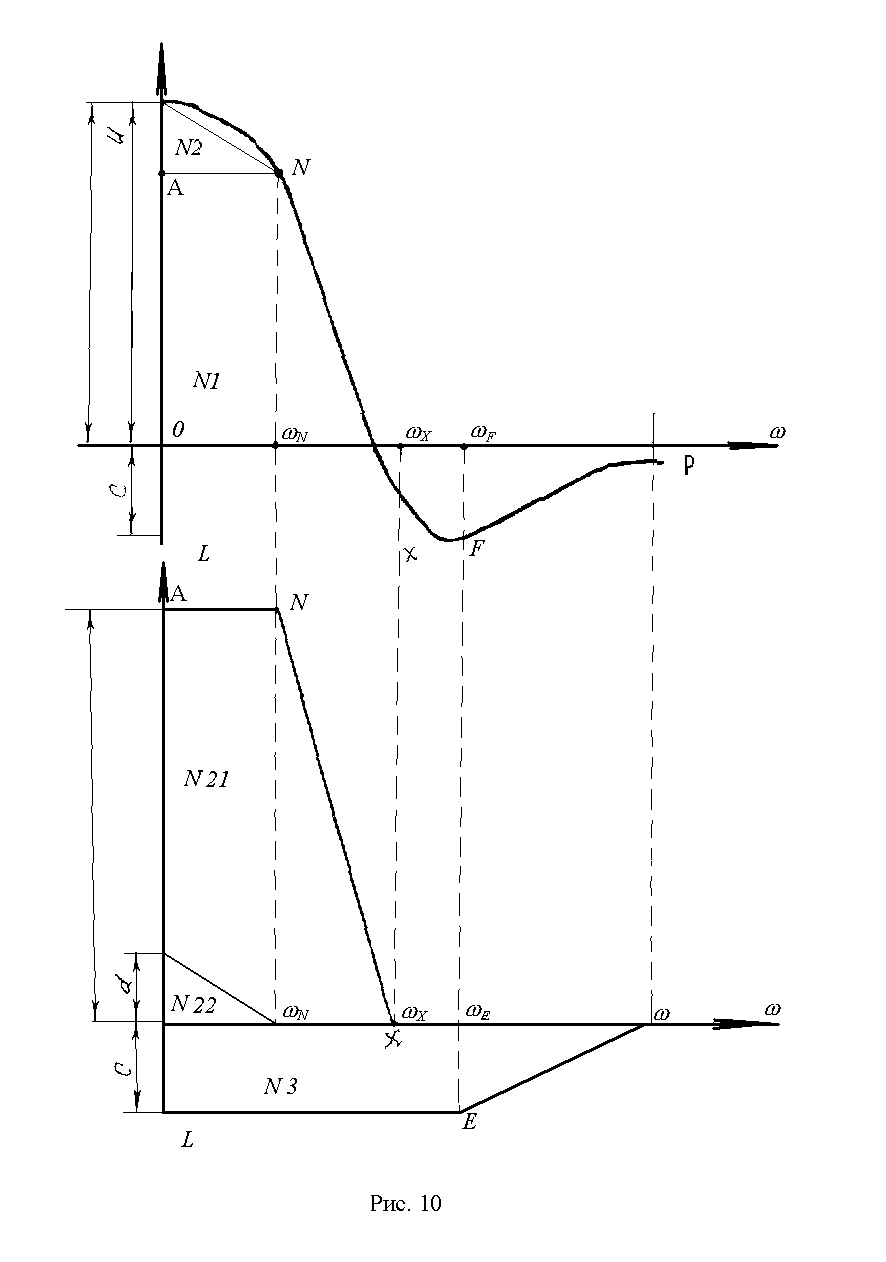
Таблица h-функций представляет собой данные расчетов переход­ных характеристик, выполненных по формуле (66) для единичных (норми­ро­ванных) трапеций, имеющих различные наклоны.

Единичная трапеция - это трапеция, у которой высота и полоса пропус­кания частот равны единице (H=1, ω0=1).

Следовательно, единичные трапеции отличаются только одним изме­няемым параметром =ωd/ω0, который может принимать значения от нуля (трапетция превращается в треугольник) до единицы (трапеция превращается в прямоугольник).

График функции h(t) представляет собой затухающие колебания для >0 и апериодический процесс для треугольника (=0). Поэтому при выборе данных для трапеций следует взять 4-5 значений из таблицы h-функций в начале переходного процесса до достижения первого макси­мума, затем выписать значения, соответствующие максимумам и мини­мумам h-функции, и по 2-3 промежуточных значений между минимумами и максимумами.

Для треугольника (=0) можно задаваться равномерными интерва­лами времени.

Для перехода от единичных трапеций к реальным необходимо определить реальное время t и ординаты реальных переходных харак­теристик x_i.

Реальное время t (графы 3, 7, 11) можно определить по формуле

, (69)

а ординаты переходных характеристик x1, x2, x3 (графы 4, 8,12) – по формуле

x_i=hH_i , (70)

где h – данные колонок 2, 6, 10; Hi – высота соответствующей трапеции или треугольника.

5. По данным таблицы на одном графике строят кривые для каждой трапеции и находят результирующую переходную характеристику x(t) алгебраическим суммированием ординат x_i(t).

Для рассматриваемого примера x(t)=∑xi(t)=x1(t)+x2(t)-x3(t) (71)

6. По характеру, продолжительности, перерегулированию и сте­пени затухания кривой x(t) анализируют качество переходного процесса.