1. Расчёт линейных непрерывных сау по заданной точности в установившемся режиме Передаточные функции сау

На рисунке 3 показана структурная схема линейной САУ с единичной обратной связью, где Хз=G ; W(p) и Woc(p) – передаточные функции элементов системы, находящихся в основном тракте и в канале главной обратной связи; Wf(p) – передаточная функция разомкнутой системы по возмущающему воздействию.

Рассмотрим воздействие по каждому входу независимо от других.

Передаточная функция замкнутой системы по управляющему воздейст­вию (при f=0) имеет вид

(1)

Передаточная функция замкнутой системы по возмущающему воздействию

(2)

При исследовании точности системы управления в установившемся режиме целесообразно располагать выражениями для передаточной функции ошибки замкнутой системы по управляющему и возмущающему воздействиям:

(3)

(4)

Если система имеет единичную обратную связь, то в формулах (1)-(4)

W_oc(p)=1.

С помощью передаточных функций замкнутой системы на основании принципа суперпозиции получаем изображения выходной величины и сигнала ошибки:

(5)

Составляющая ошибки называется ошибкой по управляющему воздействию, она зависит от управляющего воздействия; составляющая ошибки соответственно – ошибкой по возмущающему воздействию.

Определение установившихся ошибок в системах автоматического управления.

Обеспечение необходимой точности воспроизведения задающего (управляющего) сигнала в установившемся режиме – одно из основных требований, которым должна удовлетворять система автоматического управления. Для оценки точности системы определяют установившуюся ошибку, которую можно получить из (5) с помощью теоремы о конечном значении функции:

(6)

Если управляющее воздействие g(t) имеет произвольный харак­тер, то ошибку системы можно найти с помощью коэффициентов оши­бок. На основании (3) и (5) определим изображение ошибки по управ­ляющему воздействию системы с обратной связью:

(7)

Передаточную функцию представим в виде ряда

(8)

сходящегося при малых p, что соответствует установившемуся режиму или достаточно большим значениям времени.

Коэффициенты этого ряда называются коэффициентами ошибок.

Они определяются с помощью выражений

(9)

или непосредственным делением полинома числителя на полином знаменателя передаточной функции.

Коэффициенты С₀, С₁, и С_n называются соответственно коэффициентами позиционной, скоростной и ошибки от ускорения.

Выразим установившуюся ошибку через коэффициенты ошибок, управляющее воздействие и его производные с учетом приведенных формул и [1-4]:

(10)

Аналогично можно ввести понятие коэффициентов ошибок по возмущающему воздействию.

1.2 Точность сау при типовых воздействиях

Как правило, работу САУ анализируют при типовых воздействиях, близких к реальным управляющим и возмущающим воздействиям в нормальных или в наиболее трудных режимах ра­боты.

Рассмотрим установившийся режим системы с единичной обратной связью при постоянных возмущающих ( ) и управляющих ( ) воздействиях. В этом случае ошибка системы называ­ется статической [1-2] и находится с помощью выражения

(11)

В статических системах автоматического управления W(0)=k , где k. - коэффициент передачи разомкнутой системы. Составляющая статиче­ской ошибки от управляющего воздействия

(12)

Составляющая статической ошибки от возмущающего воздействия

(13)

где - коэффициент передачи системы между точками приложения возмущения и выхода системы (коэффициент передачи разомкнутой системы по возмущающему воздействию).

Кроме ошибок этих двух составляющих иногда необходимо учитывать и ошибку чувствительного элемента ч.э. который не является идеальным.

Результирующая статическая ошибка системы управления имеет вид

(14)

В астатических системах управления , поэтому составляющая ошибки , Вторая составляющая ошибки при не всегда обращается в нуль, так как возможен случай, когда и . При включении интегрирующего (астатического) звена в цепь обратной связи относительно приложенного возмущения и выхода системы статическая ошибка системы при постоянном возмущающем воздействии обращается в нуль. Однако повышение порядка астатизма в следящих системах за счет включения интегрирующих звеньев в прямой цепи системы не может исключить ошибку чувствительного элемента, которую следует рассматривать как эквивалентное постоянное возмущение.

Режим работы при постоянных управляющих и возмущающих воздействиях наиболее характерен для систем автоматической стабилизации.

Рассмотрим установившееся состояние при изменении управляющего воздействия с постоянной скоростью (где ) и при постоянном значении возмущающего воздействия , по (6) найдем установившуюся ошибку:

(15)

Система автоматического управления или следящая система, рабо­тающая в режиме слежения с постоянной скоростью, должна быть аста­ти­ческой относительно управляющего воздействия, так как первый, член выражения (15) в статической системе при W(0)=k стремится к бес­конечности.

Второе слагаемое определяет статическую ошибку системы от возму­щающего воздействия, в которую также необходимо включить ошибку чувствительного элемента.

Для системы с астатизмом первого порядка установившаяся ошибка от управляющего воздействия

(16)

где - коэффициент передачи (добротность) системы по скорости.

Ошибка называется скоростной ошибкой от управляющего воздействия.

Скоростная ошибка в системе с астатизмом второго порядка и выше равна нулю (так как ), поэтому режим с управляющим воздей­ст­вием, изменяющимся с постоянной скоростью, используется только для оценки точности следящих систем с астатизмом первого порядка.

Рассмотрим установившийся режим в системе при изменении управляю­щего воздействия с постоянным ускорением (где ) и при постоянном значении возмущающего воздействия .

Установившаяся ошибка определяется аналогично (6):

(17)

Этот режим имеет смысл только для следящих систем с астатизмом второго порядка, так как в статической и астатической системах перво­го порядка первая составляющая ошибки стремится к нулю. Ошибка по управляющему воздействию для следящих систем с астатизмом второго по­рядка имеет вид

(18)

где 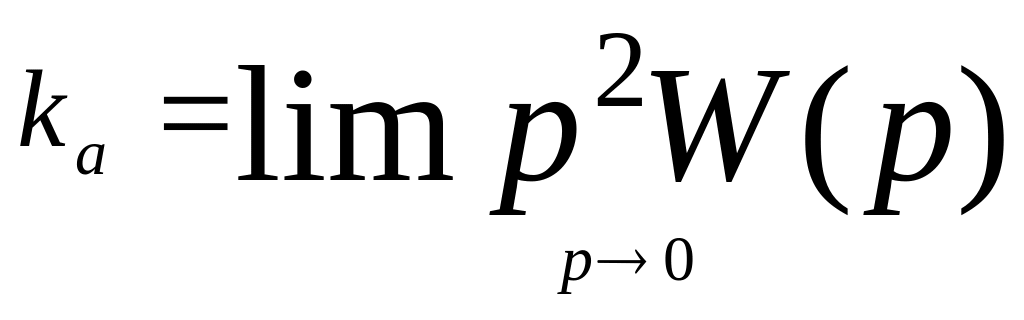- коэффициент передачи (добротность) системы по ускорению.

Ошибка называется установившейся ошибкой системы от ус­коре­ния. Этот режим работы обычно применяется для оценки точности сле­дящих систем с астатизмом второго порядка.

Второе слагаемое, как и в предыдущем случае, вместе с ошибкой чувствительного элемента определяет статическую ошибку системы от возмущающего воздействия.

Рассмотрим установившийся режим системы регулирования при изме­нении управляющего воздействия по гармоническому закону:

(19)

Предположим, что возмущающее воздействие равно нулю. В этом слу­чае ошибка в установившемся режиме также изменяется по гармо­ническому закону с частотой :

Точность системы в этом режиме можно оценить по амплитуде ошибки, которая находится из (5) подставкой р=jωk (при f=0) и опреде­лением модуля подученного выражения:

. (20)

При |W(jωk)|>>1

(21)

где R(ωk) - модуль частотной характеристики разомкнутой системы.

Выражение (21) удобно применять, если используется метод логариф­мических частотных характеристик.

В статических системах коэффициент усиления определяет значение статической ошибки. Другими словами, установившееся значение регу­ли­руемой величины будет тем меньше отличаться от своего первона­чального значения, чем большим коэффициентом усиления обладает система. Следо­вательно, с точки зрения статической точности регули­рования, коэффи­циент усиления нужно увеличивать. Однако по мере роста коэффициента усиления при прочих равных условиях ухудшается устойчивость системы.

Система неустойчива, если свободная составляющая переходного процесса от возмущающего воздействия на выходе системы с течением времени неограниченно возрастает. Поведение свободной составляю­щей зависит от расположения корней характеристического уравнения замкну­той системы на комплексной плоскости.

Правила, позволяющие определить расположение корней характерис­ти­ческого уравнения на комплексной плоскости без нахождения значений самих корней и тем самым определить устойчивость системы, называются критериями устойчивости.

2. ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ СИСТЕМЫ С ПОМОЩЬЮ КРИТЕРИЕВ

2.1. Критерий Гурвица

Устойчивость системы по критерию Гурвица исследуется с помощью характеристического уравнения замкнутой системы вида

(22)

Формулировка критерия Гурвица:

система устойчива, если при a0>0 определитель, составленный по определенному правилу из коэффициентов характеристического уравне­ния, и все его диагональные миноры больше нуля.

Определитель Гурвица составляется по следующему правилу:

1) по главной диагонали выписываются все коэффициенты характе­ристического уравнения начиная с a1;

2) места вверх от диагонали заполняются коэффициентами с возрас­тающими индексами, а вниз - с убывающими; если такие коэффициенты от­сутствуют, ставят нуль.

Для получения диагональных миноров из определителя вычеркивают нижние строки и крайние столбцы.

Пример определителя Гурвица для характеристического уравнения чет­вертого порядка:

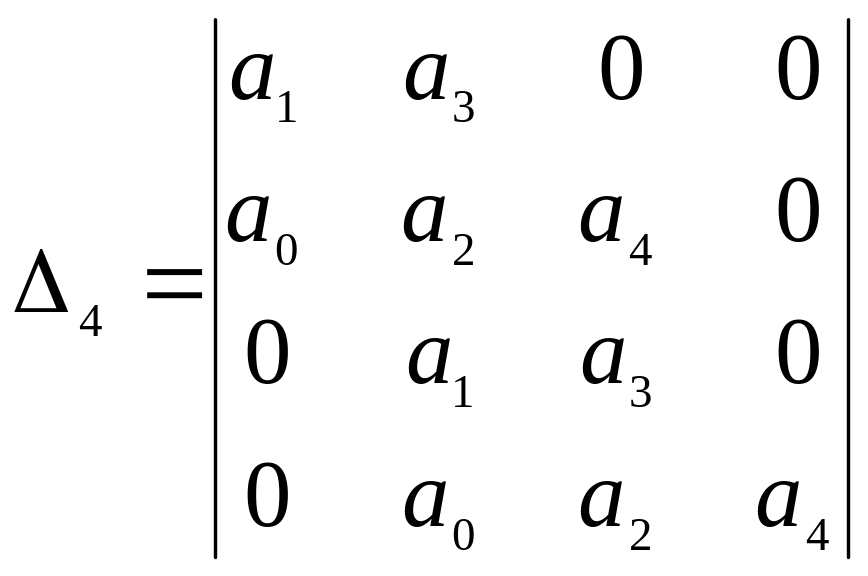(23)

Как правило, при исследовании устойчивости по критерию Гурвица не вычисляют определитель и все его диагональные миноры. Достаточ­ное условие устойчивости для системы четвертого порядка - положи­тельность всех коэффициентов и диагонального минора третьего по­рядка:

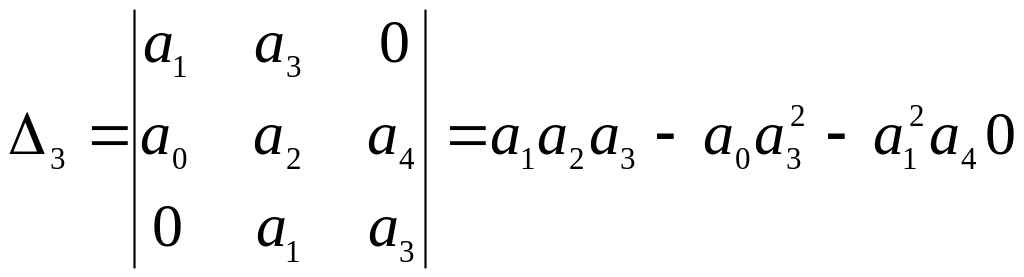(24)

2.2. Критерий Михайлова

Критерий применяется обычно при сравнительно высоких степенях характеристического уравнения. Был предложен Михай­ловым В.М. в 1938 г.

Формулировка критерия Михайлова: система автоматического управле­ния устойчива, если годограф вектора Михайлова при измене­нии частоты ω от 0 до ∞ начинается при ω=0 положительной вещественной полуоси и обходит в положительном направлении (против хода часовой стрелки) последовательно n квадрантов, нигде не обращаясь в нуль (где n– порядок характеристического уравнения системы).

Методом подстановки р=(jω) в характеристический полином

(25)

получают вектор Михайлова

(26)

Вещественные члены выражения D (jω) , получаемые при четных сте­пенях, и мнимые, получаемые при нечетных, группируются следую­щим образом:

D (jω) = А(ω)+jB(ω) , (27)

где

(28)

Годограф Михайлова имеет вид кривой, описанной концом вектора D(jω)на комплексной плоскости [A;jB] при изменении частоты ω от 0 до ∞ .

Порядок построения годографа:

1) задаются рядом значений частоты и вычисляют соответствующие им

значения A(ω) и B(ω);

2) откладывают эти значения на осях координат комплексной плос­кости;

3) соединяют полученные точки и получают искомую кривую. Вид годо­графа вектора Михайлова показан на рис. 4.

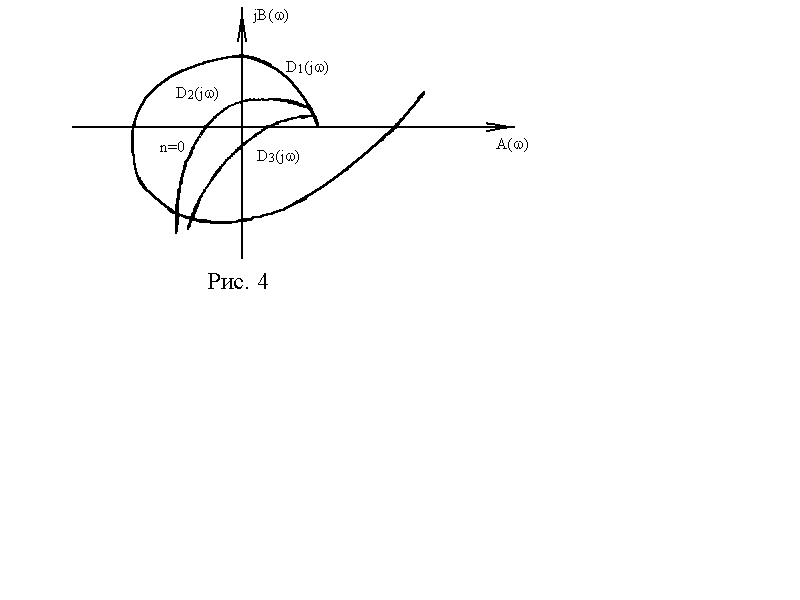
Согласно определению критерия Михайлова кривые D1(jω) и D2(jω) соответствуют устойчивой, D3(jω) – неустойчивой систе­мам.

Если годограф D(jω) проходит через начало координат, то си­стема находится на границе устойчивости.

Влияние некоторого параметра Т на устойчивость системы можно определить следующим образом. Строится ряд годографов Михайлова, каж­дый из которых соответствует определенному значению исследуе­мого па­раметра. Влияние Т на устойчивость определяют по расположе­нию го­дографов. Значение T, при котором годограф проходит через начало координат, является критическим. Однако значительно удобнее исследо­вать влияние параметров с помощью следствия критерия Ми­хайлова (вто­рая формулировка). В этом случае об устойчивости судят по виду кри­вых А(ω) и B(ω) без построения годографа Михайлова D(jω) .

Вторая формулировка критерия Михайлова: система будет устойчи­вой, если корни кривых A(ω) и B(ω) будут вещественными, т.е. будут иметь пересечения с осью ω , и перемежаю­щимися, т.е. вначале с осью ω пересекается кривая А(ω) , а затем В(ω) и т.д.

На рис. 5 показаны кривые А(ω) и B(ω) для устойчивой CAP и А1 (ω) , В₁ (ω) - для неустойчивой.

Если кривые А(ω) и B(ω) пересекаются в одной точке на оси ω , то система находится на границе устойчивости. Значение частоты, соответствующее точке пересечения кривых, называют критическим.