В курсовой работе необходимо выполнить комплекс расчётов автоматич­еской системы управления, задаваемой в виде обобщённой унифицированной алгоритмической схемы (рис. 1). Система состоит из объекта управления ОУ, исполнительного устройства ИУ, управляющего устройства и одного корректирующего устройства, включенного либо последовательно, либо встречно-параллельно в основной контур сис­темы. В зависимости от варианта задания исполнительное устройство системы может рассматриваться как идеальное интегрирующее звено или как инерционное звено первого порядка. Соответственно вся сис­тема будет астатической или статической.

На разных этапах выполнения курсовой работы автоматическую сис­тему рассматривают как линейную (с линейным преобразующим элементом ПЭ), нелинейную (введением вместо преобразующего элемента нелинейного элемента с заданным уровнем нелинейности) или импульсную (введением вместо преобразующего элемента ПЭ элемента дискретизации ИЭ).

Выходная величина объекта Х (управляемая величина системы) за­висит от управляющего воздействия  и возмущающего воздействия f .

Требуемый закон изменения величины Х определяется задающим воздействием Хз. Кроме основного возмущающего воздействия на сис­тему влияет помеха z. Поскольку на систему действуют оба возмуще­ния, а также из-за инерционности элементов системы в переходных и установившихся режимах возникает сигнал отклонения (сигнал ошибки  ).

Содержание курсовой работы

Курсовая работа состоит из девяти разделов.

1. Оценка точности системы.

Точность статической системы оценивается при ступенчатом воздействии. Точность астатической системы – при линейном воздействии. Методика расчёта точности системы приведена в (1;2).

2. Проверка устойчивости исходной системы.

Проверяется устойчивость нескорректированной системы с исходными, постоянными времени и с выбранным (по требуемой точности) значением общего передаточного коэффициента.

Устойчивость – одна из наиболее важных характеристик автоматической СУ, наряду с точностью. От устойчивости системы зависит её работоспособность. В курсовой работе необходима устойчивость сис­темы по методу, указанному в таблице выбора заданий по анализу устойчивости и качеству системы (см. табл.3).

3. Расчёт корректирующего устройства.

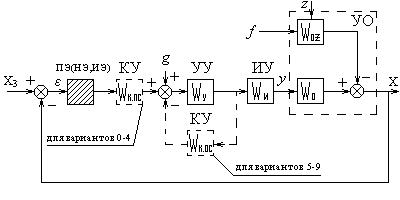
рис.1

Осуществляется с помощью логарифмических частотных характе­ристик. Результаты расчёта – передаточная функция, параметры и принципиальная схема корректирующего устройства.

Метод расчёта корректирующего устройства с помощью логарифмических частотных характеристик основан на связи переходного процесса с действительной частотной характеристикой

Р() замкнутой системы и ЛАЧХ L() разомкнутого контура. Благодаря этой связи можно по указанным показателям переходного процесса построить так называемую желаемую характеристику Lcк() – характе­ристику скорректированной системы, соответствующую требуемым показателям качества. Зная желаемую L_cк() и исходную,

Нескорректированную L_н() характеристики, можно найти требуемую характеристику корректирующего устройства L_к(). Для расчёта коррек­тирующего устройства рекомендуется использовать методику из (2;3).

При выборе корректирующего устройства по справочным таблицам допускается приближённая замена требуемой характеристики. Построе­ние характеристик разомкнутой и замкнутой систем целесообразно осуществить с применением ЭВМ.

4. Построение области устойчивости скорректированной системы.

Выполняется согласно методике описанной в (3;4).

После построения области устойчивости скорректированной сис­темы необходимо на рисунке показать точку, соответствующую принятым значениям параметров.

5. Построение графика переходного процесса и оценка качества скорректированной системы.

Необходимо построить график переходного процесса в скорректи­рованной системы, вызванного единичным ступенчатым воздействием.

Качество системы оценивается по форме переходного процесса, числу полуколебаний, первому максимальному отклонению, длительности и перерегулированию. Значение двух последних показателей сравнивают с требуемыми значениями (5;6).

6. Вычисление и минимизация квадратичной интегральной оценки при типовом воздействии.

Квадратичная интегральная оценка наиболее широко используется для исследования колебательных систем. Квадратичная оценка учитывает размер и длительность отклонений.

Квадратичная интегральная оценка вычисляется при заданном типовом (линейном или ступенчатом) воздействии (см. табл.2) при этом допускается упрощение передаточной функции скорректированной сис­темы приравниванием наименьшей постоянной времени (исходной сис­темы) к нулю.

Минимум интегральной оценки и оптимального значения передаточного коэффициента рекомендуется определить непосредственно по графику функции I=f(ку), построенного по точкам (4-6).

Вычисление и минимизация дисперсии сигнала ошибки при случайных воздействиях.

При вычислении и минимизации дисперсии сигнала ошибки скорректированной системы также рекомендуется упрощение передаточной функции и использование графика минимизированной функции Д=f(ку), построенного по точкам (1-4).

Анализ нелинейной системы.

Так как нелинейная система образована из нескорректированной системы заменой преобразующего элемента ПЭ нелинейным элементом НЭ (см. табл.4), то в начале необходимо провести алгоритмическую схему нелинейной системы, состоящей из линейной и нелинейной частей и отражающую конкретный вид статической характеристики нелинейного элемента.

Если согласно заданию нелинейная система анализируется методом фазовых траекторий, линейная часть нескорректированной системы может быть упрощена до второго порядка (приравниванием к нулю наименьшей постоянной времени) (6-9).

Анализ импульсной системы.

Импульсная система образуется из нескорректированной линейной системы заменой элемента ПЭ импульсным элементом ИЭ.

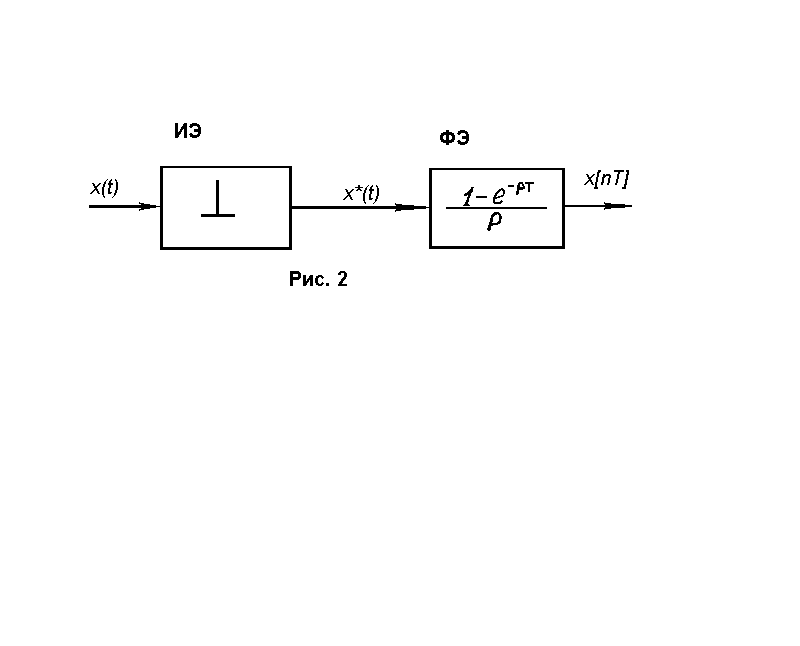
Необходимо в начале привести алгоритмическую схему импульсной системы. Импульсный элемент ИЭ (рис. 2) состоит из простейшего импульсного элемента ПИЭ («ключа») и формирующего элемента ВЭ в виде фиксатора с параметрами

К_иэ=I , н=Т , =1 .

При выполнении разделов 5,7-9, кроме основных расчётов по аналитическим выражениям рекомендуется производить моделирование системы на ЭВМ и сравнивать результаты моделирования с резуль­татами основных расчётов.