116

3.1.6. Нестационарный тепловой режим.

Нестационарное температурное поле

В нестационарном режиме температура зависит не только от координат, но и от времени: . Нестационарное температурное поле определяется решением уравнения теплопроводности совместно с условиями однозначности.

Пусть неограниченная пластина толщиной h = 2R, имеющая начальную температуру Т_о, помещена в среду с температурой Т_с и коэффициентом теплообмена  (рис. 3.12). Требуется найти нестационарное температурное поле пластины, то есть выражение для температуры в некоторой точке x в момент времени t. С учетом симметрии температурного поля относительно плоскости х = 0 задача описывается математически уравнением теплопроводности:

, (3.49)

с начальным и граничными условиями:

.

С

Рис. 3.12. Расчетная схема для определения температурного поля

формулированная задача имеет аналитическое решение:

(3.50)

где U_n(x) – функция координат зависит от формы тела и называется собственной функцией данной задачи; _n – безразмерные вещественные (действительные) числа, называемые собственными числами задачи, их значения определяются видом собственной функции и граничных условий.

Выражение для расчета температуры содержит сумму бесконечного числа членов ряда. Кроме того, в случае граничного условия III рода при вычислении каждого из членов ряда необходимо решать трансцендентное (неалгебраическое) уравнение, что представляет трудоемкую задачу. Поэтому практическое использование аналитического решения встречает значительные трудности и требует применения ЭВМ.

Рассмотренная задача относится к типовым, то есть часто встречается на практике. В связи с этим возникает необходимость иметь готовые результаты расчетов температурного поля, представленные в виде справочных данных – таблиц или графиков. Поскольку Т(х, ) – функция двух переменных, ее график представляет собой семейство кривых (зависимость Т(х) при разных фиксированных значениях  или Т() при разных х). Каждое такое семейство будет соответствовать конкретному частному решению задачи. Однако количество графиков будет зависеть от параметров, входящих в уравнение теплопроводности, и условия однозначности. В данном примере их шесть (а – коэффициент температуропроводности, входящий в уравнение, и условия однозначности: Т_о; Т_с, R,  и ). Если при составлении справочника приводить результаты для n значений каждого из параметров, потребуется построить n⁶ графиков ( при n = 3; n⁶ = 729). Очевидно, что создание такого справочника (также как и его использование) затруднительно. Справочные данные имеют смысл тогда, когда они описывают целый класс практических задач. Получить такие универсальные данные можно, если перейти к безразмерным (обобщенным) переменным и параметрам (критериям подобия).

Теория подобия широко применяется в таких областях, как гидро- и аэродинамика, конвективный тепло- и массообмен. Основная суть этой теории – сведение многопараметрической задачи к задаче, содержащей минимальное число параметров. Введем следующие безразмерные переменные:

(3.51)

Переменная  линейно связана с температурой Т и называется относительной избыточной температурой (или параметр температуры). Переменная  представляет собой относительную координату. Переменная Fо характеризует в безразмерной форме время и носит название критерия (числа) Фурье. Безразмерным параметром этой задачи является величина Вi =  R/, называемая критерием Био. Критерий Био характеризует условия теплообмена тела с окружающей средой. По его значению можно оценить, какой режим теплообмена имеет место.

Формулы обратного перехода:

(3.52)

Выразим производную температуры по времени через безразмерные переменные  и Fo:

Аналогичным путем можно получить производную температуры по координатам через безразмерные  и :

Подставляя эти выражения в уравнение теплопроводности, получим

откуда (3.53)

Начальное условие: Граничные условия:

Решением этой преобразованной к безразмерной форме задачи является обобщенная функция  = (, Fo), вид которой зависит от одного параметра – критерия В_i. Значения функции  вычислены, и результаты представлены графически в справочной литературе. Задачи с постоянными граничными условиями первого и второго рода в безразмерном виде вообще не содержат параметров.

Наиболее удобным для инженерных расчетов справочным пособием является книга А.И. Пеховича и В.М. Жидких, где приведены решения 78 типовых задач, даны таблицы теплофизических свойств различных веществ, указания по методике решения задач и другие справочные данные.

3.2. Промышленные способы подвода и отвода теплоты

(теплообмен в химико-технологических аппаратах)

3.2.1. Теплообмен в текучих средах

Проведение реакций между двумя или более реагентами, находящимися в жидком или газообразном состоянии, представляет собой один из наиболее распространенных процессов химической технологии. На полноту химического превращения в реальном реакционном аппарате (реакторе) влияют многие факторы: характер основной химической реакции, то есть зависимость скорости реакции от концентрации реагентов; тепловой эффект реакции; установившаяся в зоне реагирования температура; наличие побочных реакций; подвод (или отвод) теплоты от реакционной массы; количество подаваемых в зону реакции реагирующих веществ и время их пребывания в зоне реакции; характер гидродинамического перемешивания реакционной массы и т.д.

Для полного анализа химических, физико-химических и физических процессов в гомогенном жидкофазном реакторе, когда химическая реакция не сопровождается образованием паровой или твердой фаз, необходимо иметь: 1) стехиометрическое уравнение реакции и константу ее равновесия; 2) уравнения неразрывности всех компонентов с учетом источника (стока) массы за счет химической реакции; 3) уравнение гидродинамики потоков с учетом возможного изменения объемов продуктов реакции; 4) уравнение переноса энергии с учетом источника (стока) теплоты за счет теплоты реакции; 5) уравнение переноса реагирующих компонентов за счет конвективного и диффузионного механизмов, также с учетом стока (источника) массы; 6) кинетическое уравнение химической реакции, определяющее зависимость скорости химического превращения от концентрации реагентов; 7) зависимость константы скорости реакции от температуры и энергии активации (уравнение Аррениуса).

Такая система алгебраических и дифференциальных уравнений с соответствующими начальными и граничными условиями полностью определяет поля температуры, концентраций и скоростей движения реагентов в реакционном аппарате. Усреднение этих полей на выходе из аппарата позволяет получить интегральную степень превращения, достигаемую при заданных условиях работы.

Однако решение общей системы уравнений, описывающей протекающий в реакторе процесс, не представляется возможным ввиду значительной сложности нелинейных дифференциальных уравнений переноса с коэффициентами (вязкость, коэффициенты теплопроводности, диффузии и т.д.), зависящими от искомого распределения температуры.

Как известно, при анализе сложных процессов, нужны приемлемые упрощения их описания. В теории химических реакторов принято полагать, что вместо сложного химического, теплового и диффузионного взаимодействия можно анализировать более простые предельные варианты процессов: 1) скорость собственно химической реакции значительно меньше скорости подачи реагентов в аппарат и транспортировки их из основной массы потока в зону непосредственно реагирования, при этом интегральная скорость всего процесса не зависит от интенсивности массообменных процессов, а определяется кинетикой химической реакции (концентрацией и температурой реагентов) – это так называемая кинетическая область протекания процесса; 2) скорость химической реакции велика, и общий темп химического превращения определяется скоростью транспортировки реагентов в зону реагирования – диффузная область; 3) скорость реакции зависит в сравнимой степени как от диффузионных процессов, так и от кинетики химической реакции – смешанная область.

В некоторых простых случаях быстрого протекания химических и диффузионных процессов общую степень превращения может лимитировать скорость подвода реагентов в реактор (балансовая задача).

Уравнение скорости химической реакции (быстроты изменения концентраций реагентов со временем) записывается в степенной форме относительно концентрации реагентов:

(3.54)

где ₁ и ₂ – порядки реакции по компонентам 1 и 2, получаемые, как правило, опытным путем; k – константа скорости реакции.

Общепринятой является запись температурной зависимости k в виде уравнения Аррениуса

(3.55)

где Е – энергия активации данной реакции; R – газовая постоянная; k_o – предэкспоненциальный множитель, зависящий от вероятности реагирования молекул реагентов при их столкновении. Значение k_o определяется опытным путем для конкретных реакций, проводимых при разных температурах Т (в К).

При анализе температурных режимов работы реакционных аппаратов принято рассматривать следующие предельные и промежуточные варианты:

1) изотермический режим, при котором постоянство температуры во всем реакционном объеме аппарата поддерживается за счет достаточно интенсивного теплообмена с окружающей средой, позволяющего подводить к реакционной массе (или отводить от нее) всю поглощаемую (или выделяемую) теплоту химической реакции; кроме того, должно быть обеспечено полное перемешивание реагирующей массы, чтобы не было температурных градиентов;

2) адиабатический режим предполагает отсутствие теплообмена между зоной реакции и окружающей средой, при этом выделяющаяся за счет реакции теплота идет на разогрев при экзотермических реакциях, а при эндотермических реакциях происходит охлаждение реакционной массы. В проточных реакторах вытеснения температура увеличивается или падает по длине адиабатического реактора;

3) реальный промежуточный режим соответствует частичному отводу теплоты реакции. При этом за счет изменения интенсивности теплоотвода оказывается возможным регулировать температуру реакционной массы во времени для периодических процессов либо по длине проточного аппарата непрерывного действия;

4) при автотермическом режиме теплота реакции используется для поддержания ее температурного режима. Практически это означает подогрев исходных реагентов продуктами реакции, разогретыми в результате экзотермического процесса.

Из уравнений химической кинетики следует, что температура оказывает наиболее значительное влияние на скорость химической реакции в кинетической области процесса.

З

Рис. 3.13. Зависимость степени превращения

от температуры

для необратимых реакций

ависимость степени превращения от температуры для необратимых реакций при некоторых временах процесса реагирования t₁ > t₂ представлена на рис. 3.13. При фиксированном времени реагирования в случае низкой температуры степень превращения мала. Затем она значительно увеличивается с возрастанием Т, асимптотически приближаясь к полной степени превращения (х = 1). По мере увеличения времени, предоставленного для проведения реакции, можно либо увеличить степень превращения при сохранении температуры реакции, либо уменьшить Т при сохранении необходимой конечной степени превращения. Для проточного реактора увеличение времени реагирования может быть достигнуто увеличением объема реактора или снижением его производительности.

Д

Рис. 3.14. Зависимость степени превращения

от температуры для обратимых реакций

ля обратимых реакций влияние температуры на степень превращения также имеет S-образный характер, но верхний предел кривых соответствует не полной степени превращения, а равновесным концентрациям, зависящим, в свою очередь, от температуры реакции. Кривая равновесия представлена огибающей пунктирной линией (рис. 3.14).

Для экзотермической обратимой реакции определить оптимальную температуру, при которой скорость будет максимальной, можно, если, записав уравнение скорости обратимой реакции, приравнять к нулю производную r/T = 0.

(3.56)

(3.57)

Определение температурного режима химических аппаратов с гомогенной реакцией

Наиболее распространенными в химической промышленности являются химические реакторы непрерывного действия с интенсивным перемешиванием реакционной массы и теплоотводом (рис. 3.15).

П

Рис. 3.15. Схема химического реактора

непрерывного действия

еремешивание используется для создания однородных концентрационных и температур-ных условий по всему объему аппарата и интенсификации теплообмена реакционной массы с теплообменной поверхностью.

Отвод теплоты при проведении экзотермических реакций обычно применяется для того, чтобы избежать перегрева реакционной массы и не допустить, таким образом, нежелательных побочных реакций, фазовых переходов, термического разложения продуктов и т.д.

Рассмотрим необратимую экзотермическую реакцию первого порядка по концентрации основного компонента С:

(3.58)

Количество теплоты в единицу времени, поступающей в реактор, складывается из теплоты входящего потока исходных реагентов Q₁ = M₁с₁T₁ и теплоты, выделяющейся в результате химической реакции Q_х.р= hrV, где V – объем, занимаемый реагирующей массой.

Из реактора теплота отводится с уходящим потоком продуктов реакции Q₂ = M₂с₂T и за счет теплопередачи через стенку аппарата Q_т.о= к F(T ), где к – коэффициент теплопередачи, F – площадь теплоотводящей поверхности, – среднее значение температуры хладоагента.

Таким образом,

Q₁ + Q_x.p = Q₂ + Q_т.о. (3.59)

(3.60)

откуда

Концентрация С определяется из уравнения материального баланса реактора целевому компоненту:

M₁C₁ - rV = M₂C или

(3.61)

, (3.62)

где М₁ – расход (м³/с) исходных реагентов; М₂ – расход продуктов реакции; С₁ – концентрация исходных реагентов; С – концентрация целевого компонента (продукта); с₁ и с₂ – удельные (объемные) теплоемкости исходных реагентов и продуктов реакции соответственно; h – удельная теплота экзотермической реакции, Дж/кг.

Уравнение (3.62) может быть решено относительно температуры процесса Т, которая установится для реакционной массы при всех заданных величинах.

Р ассмотрим графический способ определения температуры реакции по этому уравнению (рис. 3.16). Графическое изображение правой части уравнения представляет собой прямые линии с различными углами наклона в зависимости от значений входящих в нее величин (М₂,с₂, k, F). График левой части представляет собой S-образную кривую зависимости тепловыделения от температуры. Решениями уравнения служат значения абсцисс точек пересечения графиков левой и правой частей уравнения.

В

Рис. 3.16. Графический способ определения температуры для экзотермической реакции

случае, когда прямая линия теплоотвода пересекает кривую тепловыделения в трех точках, средняя точка b соответствует неустойчивому тепловому режиму, т.к. случайное увеличение температуры усилит тепловыделение значительнее, чем увеличится теплоотвод, что приведет к самопроизвольному возрастанию температуры до точки С. Если в точке b произойдет самопроизвольное падение температуры, то теплоотвод слева от b превысит выделение теплоты, что приведет к дальнейшему уменьшению температуры до точки а. В точках, соответствующих устойчивым температурным режимам (а, с), случайное увеличение температуры, наоборот, приведет к большему теплоотводу по сравнению с тепловыделением, что уменьшит температуру реакционной массы до стационарного значения.

Левая и правая линии дают только по одному устойчивому температурному режиму. Точки пересечения в верхней правой части кривых соответствуют установившемуся высокотемпературному процессу с высокой скоростью химической реакции и, соответственно, высокой степенью превращения. Высокие скорости теплоотвода (левая прямая) соответствуют низкотемпературному реагированию с малой скоростью химического превращения. Пунктирное продолжение кривой тепловыделения соответствует обратимой реакции. После нахождения величины Т определяется концентрация С.

Аналогичный анализ химических реакций произвольного порядка приводит к более сложной алгебраической процедуре отыскания температуры устойчивого процесса.

Для адиабатического реактора (к = 0) в уравнении теплового баланса исчезает слагаемое, соответствующее охлаждению зоны реакции, а порядок расчета остается прежним.

Д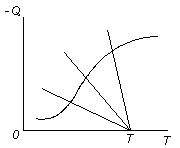 ля эндотермических реакций с подводом теплоты тангенс угла наклона линии теплоподвода изменяет знак. Точка пересечения кривой теплопоглощения и линии подвода теплоты будет только одна, т.е. при подводе теплоты в зону эндотермической реакции любые температурные режимы оказываются устойчивыми (рис. 3.17).

В

Рис. 3.17. Графический способ определения температуры

для эндотермической реакции

общем случае для непрерывного реактора полного смешения возможны различные варианты температурных режимов, о чем можно судить с достаточной полнотой лишь по результатам конкретного анализа уравнений химической кинетики, теплового и материального балансов.