Горизонталь құбыр арқылы сұйықтың ағысы. Пуазейль заңы.

Қанайналым жүйесінің физикалық негіздерін пайдаланып, қимасы тұрақты горизонталь құбыр арқылыжұғатын, тұтқырлы сұйықтың ағысын қарастырайық. Біршама кіші жылдамдықта сұйықтың ағысы ламинарлы болады: құбырдың қабырғасына іргелес жатқан молекула қабаты оған жабысып, қозғалмайды. Молекуланың келесі қабаты қысым күштері әсері мен қабаттар арасындағы ішкі үйкеліс күшінің кері әсер етуінен құбыр қабырғасына жақын жатқан қабатқа салыстырмалы ығысып, құбыр қабырғасына қатысты біраз кіші жылдамдықпен қозғала бастайды. Молекуланың әрбір келесі қабаты алдындағы қабатқа салыстырмалы ығыса отырып, құбыр қабырғасына қатысты қозғала отырып, оның жылдамдығы артады. Құбырдың центрінде ол максимал шамаға жетеді.

О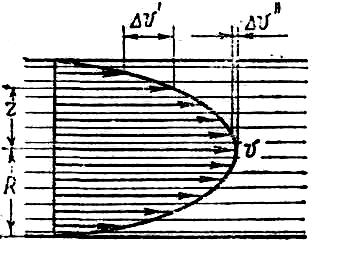 сы құбылысты математикалық талдау мынаны көрсетті: дөңгелек құбырдың қимасымен жылдамдықтардың үлестірілуі параболалық сипатқа ие болады: Құбыр центріндегі максимал жылдамдық: . Осы формулалардағы — ұзындығы болатын құбырдың бастапқы және соңғы бөліктеріндегі қысымдар;

- сұйықтың тұтқырлық коэффициенті; жидкости, R – құбырдың радиусы трубы; r – сұйықтың қарастырып отырған қабатының радиусы.

Ламинарлы ағыс қабырғалары тегіс, көлденең қимасының кенет өзгерісі болмағанда, кенеттен майысуы болмағанда, көптеген тармақтары болмаған жағдайдағы құбырларда орындалады. Осы шарттар бұзылғанда, әсіресе үлкен жылдамдықта сұйықтың ағыны турбуленттіге ауысады: осы кезде сұйық бөлшектерінің жылдамдығы ретсіз өзгеріп, жергілікті құйындар пайда болады- сұйық бөлшектерінің араласуы орындалады.

Турбулентті ағысқа тән сипат- бөлшектердің тербелмелі қозғалысын тудыратын сұйықтағы қысымның жергілікті өзгерісі болып табылады. Осы тербелмелі қозғалыс дыбыстық құбылыстарымен сүйемелденеді (сыбдыр, шу т.б.). Осының салдарынан турбулентті ағысты оңай байқалады. Турбулентті ағыс сұйықтың қозғалысы кезінде энергияның қосымша шығындалуымен байланысты. Сондықтан қанайналым жүйесінде бұл жүрекке қосымша жүктеменің түсуіне әкеліп соғуы мүмкін. Қанның турбулентті ағысы кезінде пайда болатын шу ауруды диагностикалауда пайдаланылуы мүмкін. Жүрек қақпашаларының жарақаттануы кезінде, қанның турбулентті ағысы тудыратын жүрек шулары пайда болады. Аортадағы қанның турбулентті ағысы ең алдымен, аортаға енетін жердегі қанның турбуленттілігінен тууы мүмкін: қанның қарыншадан аортаға ығыстырыуы кезінде, ағыстың құйындары бар болады. Тамырлардың тармақталу жерлерінде, қан ағысының жылдамдығы артқанда, артериялардағы ағыс

турбулентті болуы мүмкін. Турбулентті ағыс қантамырының тарылу жерінде пайда болуы мүмкін, мысалы, тромбтың пайда болуы кезінде.

ламинарлы ағыстың турбулентті ағысқа айналу жылдамдығын Рейнольдс санымен (Re- шексіз шама) анықтауға болады. Ол мынаған тең: ; мұндағы

- сұйықтың тығыздығы, - тұтқырлығы, D- құбыр диаметрі. Түзу, тегіс құбыр үшін

. Егер , онда ағыс турбулентті ағысқа айналады. Қанның тамырлармен ағысы қанның тұтқырлығына байланысты, ол не ламинарлы не турбулентті болуы мүмкін. Қанның ламинарлы ағысы жүрекке аз жүктеме түсіреді, өйткені ол кезде жүректің жұмысы қанағысының көлемдік жылдамдығына тура пропорционал болады. Ал қанның турбулентті қозғалысы кезінде, осы параметрлер арасында квадраттық байланыс орнайды (А~ Q^1,8) .

Горизонталь кұбыр арқылы реал сұйықтың ағысы кезінде, сұйық бөлшектерінің потенциалдық энергиясы ішкі үйкелісті жою жұмысына үшін жұмсалады. Сол себепті құбыр бойындағы статикалық қысым біртіндеп төмендейді.

Сұйықтың ағысын қамтамасыз ету үшін, құбырдың басында құбырдың барлық бойында қысымның төмендеуінен біршама артық болатын қысымды тудыру керек. Қимасы тұрақты болатын құбырда қысым бірқалыпты төмендейді.

Пуазейль тәжірибе жүзінде қимасы тұрақты, кең емес горизонталь, дөңгелек құбырмен сұйықтың ламинарлы ағысының орташа жылдамдығы құбырға енетін және одан шығатын жерлеріндегі қысымдардың айырмасына, құбыр радиусының квадратына тура пропорционал, ал құбырдың ұзындығы ( ) мен сұйықтың тұтқырлық ( ) коэффициентіне кері пропорционал болатындығын тағайындады (Пуазейль заңы): ;

Кейінірек құбырдың қимасымен жылдамдықтардың үлестірілу заңын пайдаланып, Гаген осы формуланы теориялық жолмен қорытып шығарды.

Сұйық ағысының орташа жылдамдығы қимасы S құбырмен бірлік уақытта ағатын сұйықтың көлемін Q анықтайды: мұндағы ; Ендеше ;

Осы формула әдетте Гаген — Пуазейль формуласы деп аталады. Оны мына түрде де жазуға болады: , мұндағы

шамасы гидравликалық кедергі деп аталады. Ол радиустың төртінші дәрежесіне кері пропорционал, сол себепті құбыр радиусы кішірейгенде, ол шама өте едәуір артады.