6. Воздействие колебаний сложной

ФОРМЫ НА ЛИНЕЙНЫЕ ЦЕПИ

6.1. Задача расчета реакции цепи на сложное входное

воздействие

Достаточно часто возникает необходимость расчета результата воздействия на четырехполюсник входного сигнала сложной (негармонической) формы, как показано на рис. 6.1.

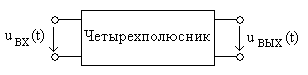
Рис. 6.1

Если бы входной сигнал был гармоническим, то для расчета можно было бы использовать метод комплексных амплитуд, тогда

, (6.1)

где и - комплексные амплитуды входного и выходного гармонических сигналов, а - комплексный коэффициент передачи цепи.

Для негармонических сигналов расчет существенно усложняется и могут использоваться различные методы.

6.2. Спектральный метод расчета

Если на вход цепи воздействует сложное (негармоническое) напряжение, то расчет выходного сигнала можно провести, используя методы спектрального анализа.

91

Для периодического входного сигнала необходимо определить комплексные амплитуды его гармоник . Свойства цепи описываются комплексным коэффициентом передачи . Тогда комплексные амплитуды гармоник выходного сигнала равны

. (6.2)

Используя ряд Фурье в комплексной форме

, (6.3)

можно получить выражение для мгновенных значений выходного сигнала.

В качестве примера рассмотрим входной сигнал вида рис. 6.2а, воздействующий на цепь, показанную на рис. 6.2б.

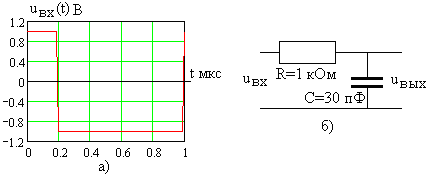
Рис. 6.2

Амплитудно-частотная характеристика цепи показана на рис. 6.3а, полоса пропускания равна 5,3 МГц, а спектр амплитуд входного сигнала – на рис. 6.3б в виде вертикальных

92

столбиков ( - номер гармоники). На рис. 6.3б сплошной линией показан спектр амплитуд выходного сигнала цепи.

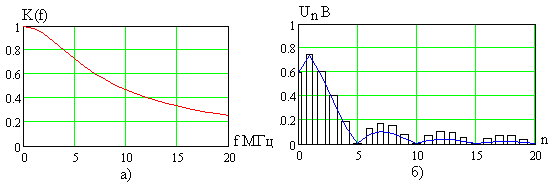
Рис. 6.3

Выходной сигнал показан на рис. 6.4. Пунктиром показан результат суммирования большого числа ( ) гармоник, а сплошной линией – постоянной составляющей и только первых трех гармоник.

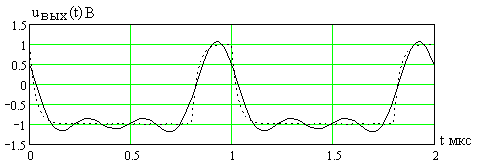
Рис. 6.4

Полученные результаты показывают, что спектральный метод позволяет определить спектр выходного сигнала (рис. 6.3б) и проанализировать влияние на него частотных свойств цепи (цепь на рис. 6.3а «заваливает» высшие гармоники сигнала), что часто является целью анализа. Суммирование сравнительно небольшого числа гармоник выходного сигнала позво-

93

ляет получить наглядные результаты влияния цепи на его временную диаграмму.

Для спектрального описания одиночного (непериодического) входного сигнала используется полная комплексная спектральная плотность , а частотные свойства цепи описываются комплексным коэффициентом передачи . Полная комплексная спектральная плотность выходного сигнала определяется выражением

. (6.4)

Рассмотрим воздействие на цепь, показанную на рис. 6.5а экспоненциального импульса вида рис. 6.5б при 1/с,

. (6.5)

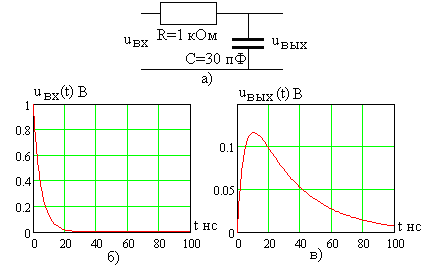
Рис. 6.5

94

Комплексный коэффициент передачи рассматриваемой цепи равен

. (6.6)

Полная комплексная спектральная плотность входного воздействия определяется выражением

, (6.7)

тогда для спектральной плотности выходного сигнала получим

. (6.8)

С использованием преобразования Лапласа (табл. 3.1) при замене можно показать, что обратное преобразование Фурье от (6.8) равно

. (6.9)

(проведите расчет самостоятельно). Зависимость выходного сигнала от времени приведена на рис. 6.5в.

6.3. Операторный метод расчета

Операторный метод расчета реакции цепи на сложное входное воздействие применим для сигналов , удовлетворяющих условию

. (6.10)

95

Для входного сигнала определяем его изображение по Лапласу . Свойства цепи полностью определяются ее операторным коэффициентом передачи , тогда изображение по Лапласу выходного сигнала равно

. (6.11)

Выходной сигнал является оригиналом от изображения вида (6.5).

В качестве примера рассмотрим цепь, показанную на рис. 6.5а при входном воздействии (6.5) на рис. 6.5б. Его изображение по Лапласу согласно табл. 3.1 имеет вид

, (6.12)

а операторный коэффициент передачи цепи равен

. (6.13)

Тогда из (6.11) получим

. (6.14)

Оригинал (6.14) определяется по табл. 3.1 и равен (6.9). Временная диаграмма выходного сигнала показана на рис. 6.5в.

Частотный и операторный методы универсальны, однако при сложном входном воздействии и сложной цепи возникают математические трудности с вычислением прямого и обратного преобразований.

96

6.4. Временные характеристики цепи

Свойства электрической цепи могут быть описаны во временной области в виде переходной и импульсной характеристик.

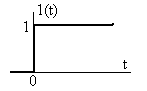Переходная характеристика цепи – это отношение реакции цепи на входное воздействие в виде единичной функции (функции Хевисайда) к единице размерности входного воздействия (1 В или 1 А). График единичной функции (функции Хевисайда) по- Рис. 6.6

казан на рис. 6.6. .

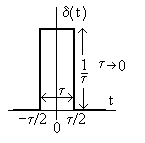Импульсная характеристика цепи - это отношение реакции цепи на входное воздействие в виде единичного импульса (функции Дирака или -функции) к единице размерности входного воздействия (1 В или 1 А). График -функции Дирака показан на рис. 6.7, она представляет собой прямоугольный импульс длительностью и амплитудой при , ее размер-ность равна 1/с. Входное воздействие Рис. 6.7.

имеет размерность сигнала ( 1 В или

1 А), деленную на секунду.

Переходная характеристика безразмерна, а импульсная измеряется в 1/с.

Временные характеристики цепи определяются через операторный коэффициент передачи с помощью преобразования Лапласа:

- импульсная характеристика является оригиналом операторного коэффициента передачи,

; (6.15)

97

- переходная характеристика является оригиналом операторного коэффициента передачи, деленного на ,

; (6.16)

В качестве примера рассмотрим цепь, показанную на рис. 6.5а, ее операторный коэффициент передачи определяется выражением (6.13), тогда

, (6.17)

. (6.18)

В результате согласно (6.15) из (6.17) и табл. 3.1. получим

, (6.19)

а согласно (6.16) из (6.18) соответственно

. (6.20)

Переходная и импульсная характеристики связаны соотношением

. (6.21)

98

Графики временных характеристик при кОм и пФ показаны на рис. 6.8.

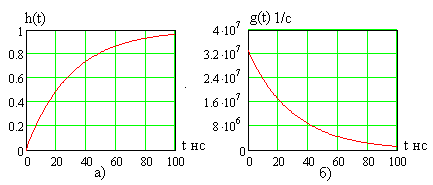
Рис. 6.8

Как видно, при воздействии в момент времени на вход цепи рис. 6.5а скачка напряжения в 1 В емкость заряжается по экспоненциальному закону до напряжения 1 В.

При подаче на вход сигнала в виде -функции (бесконечно короткого импульса) емкость мгновенно заряжается до напряжения, которое можно определить следующим образом. При малой длительности импульса напряжения с амплитудой, численно равной , емкость представляет собой короткое замыкание, а ток ее заряда равен . С другой стороны, ток емкости связан с напряжением емкости выражением

,

тогда получим уравнение

,

из которого определяется напряжение на емкости

.

99

По окончании действия импульса получим

.

а затем емкость экспоненциально разряжается, как показано на рис. 6.8б.

Переходная и импульсная характеристики используются при временном методе анализа реакции цепи на сложное входное воздействие.

6.5. Временной метод расчета

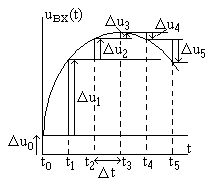Рассмотрим входное напряжение и представим его в виде суммы ступенчатых функций, как в качестве примера показано на рис. 6.9. Сигнал квантуется по времени с интервалом и в моменты квантования к предыдущему значению функции добавляется ступенька величиной соответственно. Ступеньку величиной , возникающую в

Рис. 6.9 момент времени , можно

записать в виде .

Тогда входной сигнал можно приближенно записать в виде

, (6.22)

где - целое число интервалов времени , находящихся в интервале времени от 0 до , а . Описание входно-

100

го сигнала (6.22) будет точным при .

Согласно (6.22) входной сигнал представляется взвешенной суммой единичных функций (функций Хевисайда). В соответствии с принципом наложения и определением переходной характеристики реакция цепи на взвешенную сумму единичных функций равна сумме переходных характеристик с теми же весами,

, (6.23)

где . При суммирование заменяется интегрированием и из (6.23) с учетом

(6.24)

получим

, (6.25)

(дискретная переменная заменяется непрерывной переменной ). Выражение (6.25) можно преобразовать к виду

, (6.26)

где не требуется дифференцирования входного сигнала. Это удобно, если входной сигнал изменяется скачкообразно.

Полученные выражения (6.25) или (6.26) для расчета реакции цепи на сложной входное воздействие называют интегралом Дюамеля.

В качестве примера рассмотрим цепь на рис. 6.5а при воздействии на нее сигнала (6.5), показанного ан рис. 6.5б. Пе-

101

реходная и импульсная характеристики имеют вид (6.19) и (6.20) соответственно. Подставляя (6.5), (6.19) и (6.20) в (6.26), с учетом получим

. (6.27)

Учитывая, что переменная не зависит от переменной интегрирования и соответствующая экспонента может быть вынесена за знак интеграла, получим

(6.28)

Полученное выражение совпадает с (6.9), соответствующий график показан на рис. 6.5в.

Рассмотрим воздействие на RC цепь рис.6.10б одиночного прямоугольного импульса длительностью , показанного на рис. 6.10а.

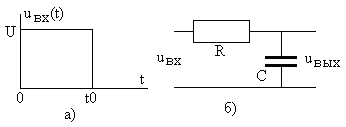
Рис. 6.10

102

Переходная и импульсная характеристики описываются выражениями (6.19) и (6.20). На интервале времени от 0 до входной сигнал равен , тогда из (6.26) получим

(6.29)

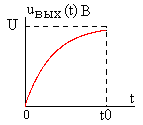
Зависимость при показана на рис. 6.11.

При выражение (6.29) неприменимо. Из (6.26) в этом случае получим интеграл, отличающийся от исходного выражения в (6.29) верхним

пределом, Рис. 6.11

(6.30)

Зависимость при (6.30) показана на рис. 6.12а.

103

Полная временная диаграмма выходного сигнала приведена на рис. 6.12б.

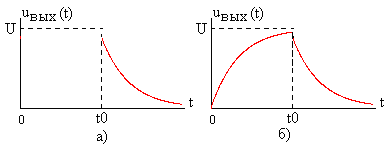
Рис. 6.12

Семейство временных диаграмм выходных сигналов RC-цепи показано на рис. 6.13 при В, мс для различных значений постоянной времени цепи . С ростом повышается инерционность цепи (уменьшается полоса пропускания фильтра нижних частот) и наблюдается сильное «сглаживание» входного прямоугольного импульса.

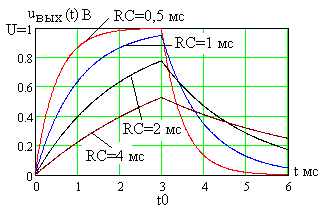
Рис. 6.13

Как видно, временной метод является весьма эффек-

104

тивным для расчета реакции цепи на сложное входное воздействие.

6.6. Задания для самостоятельного решения

Задание 6.1. Частотным и операторным методами рассчитайте выходное напряжение в цепях на рис. 6.14б и рис. 6.14в при воздействии входного напряжения, показанного на рис. 6.14а.

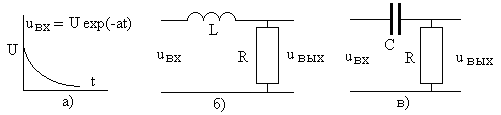
Рис. 6.14

Задание 6.2. Для цепей на рис. 6.14б и рис. 6.14в определите переходную и импульсную характеристики, постройте их графики, проведите физический анализ.

Задание 6.3. Выполните задание 6.1 методом интеграла Дюамеля.

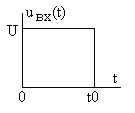
Задание 6.4. Рассчитайте реакцию цепей, показанных на рис. 6.14б и рис. 6.14в, на входное воздействие вида рис. 6.15 методом интеграла Дюамеля. Постройте временные диаграммы, проведите их физический анализ.

Рис. 6.15

105