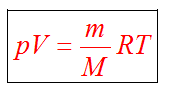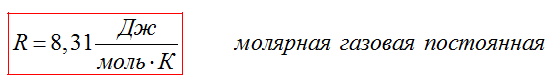1.Содержание науки «Теплотехника» и ее роль в подготовке инженерных кадров.

Теплотехника — общетехническая дисциплина, изучающая методы получения, преобразования, передачи и использования теплоты, а также принцип действия и конструктивные особенности тепло- и парогенераторов тепловых машин, агрегатов и устройств. Теоретическими разделами теплотехники, в которых исследуются законы превращения и свойства тепловой энергии, а также процессы распространения теплоты являются техническая термодинамика и теория теплообмена. В развитии теплотехники и её теоретических основ большая заслуга принадлежит российским учёным. Д. И. Менделеев провёл фундаментальные работы по общей теории теплоёмкостей и установил существование для каждого вещества критической температуры. М. В. Ломоносов создал основы молекулярно-кинетической теории вещества и установил взаимосвязь между тепловой и механической энергией.

Современная техника требует от инженера глубокого знания тепловых процессов, происходящих в различных тепловых машинах и аппаратах пищевых производств, предусматривает самое широкое использование теплоты для технологических целей.

2.Адиабатный и политропный процессы.

Адиабатическим называется процесс, при котором отсутствует теплообмен (δQ=0) между системой и окружающей средой. Адиабатическим процессами можно считать все быстропротекающие процессы. Таковым, например, можно считать процесс распространения звука в среде, так как скорость распространения звуковой волны настолько большая по значению, что обмен энергией между средой и волной произойти не успевает. Адиабатические процессы происходят в двигателях внутреннего сгорания (сжатие и расширение горючей смеси в цилиндрах), в холодильных установках и т. д.Из первого начала термодинамики (δQ=dU+δA) для адиабатического процесса следует, что

Можно записать и в интегральной форме:

Если вещество расширяется и совершает работу над внешними телами, то и, как следует

т. е. внутренняя энергия вещества уменьшается. Это и понятно: в адиабатном процессе к системе нет притока теплоты извне и единственный источник энергии для совершения работы – это внутренняя энергия самой системы. Соотношения справедливы для любых адиабатных процессов: равновесных или неравновесных, для любых веществ, находящихся в любых агрегатных состояниях, так как они являются следствием закона сохранения энергии. Для идеального газа:

Политропный процесс, политропический процесс — термодинамический процесс, во время которого удельная теплоёмкость газа остаётся неизменной.В соответствии с сущностью понятия теплоёмкости предельными частными явлениями политропного процесса являются изотермический процесс и адиабатный процесс.В случае идеального газа, изобарный процесс и изохорный процесс также являются политропными (удельные теплоёмкости идеального газа при постоянном объёме и постоянном давлении соответственно равны и и не меняются при изменении термодинамических параметров)

Показатель политропы: Кривая на термодинамических диаграммах, изображающая политропный процесс, называется «политропа». Для идеального газа уравнение политропы может быть записано в виде: где р — давление, V — объем газа, n — «показатель политропы». n=(С—Сp)/(С—СV) Здесь — теплоёмкость газа в данном процессе,

и — теплоемкости того же газа, соответственно, при постоянном давлении и объеме.

3.Формулировка 1-го закона термодинамики и его математическое выражение.

Первое начало термодинамики выражает универсальный закон сохранения энергии применительно к задачам термодинамики и исключает возможность создания вечного двигателя первого рода, то есть устройства, способного совершать работу без соответствующих затрат энергии.

Внутреннюю энергию U термодинамической системы можно изменить двумя способами, совершая над ней работу или посредством теплообмена с окружающей средой. Первое начало термодинамики утверждает, что теплота, полученная системой, идёт на увеличение внутренней энергии системы и на совершение этой системой работы, что можно записать как δQ = δA + dU. Здесь dU — полный дифференциал внутренней энергии системы, δQ — элементарное количество теплоты, переданное системе, а δA — бесконечно малая или элементарная работа, совершённая системой. Так как работа и теплота не являются функциями состояния, а зависят от способа перехода системы из одного состояния в другое, применяется запись с символом δ, чтобы подчеркнуть, что δQ и δA — это бесконечно малые величины, которые нельзя считать дифференциалами какой-либо функции.

Знаки при δQ и δA в приведённом выше соотношении выражают соглашение о том, что положительной считают работу, совершаемую системой, и теплоту, получаемую системой, принятое в большинстве современных работ по термодинамике.

Если система совершает только механическую работу вследствие изменения её объёма, то элементарная работа записывается как δA = P dV, где dV — приращение объёма. В квазистатических процессах эта работа равна работе внешних сил над системой, взятой с обратным знаком: δAвнутр = –δAвнеш, но для неквазистатических процессов это соотношение не выполняется. В общем случае элементарная работа записывается как сумма δA = A1 da1 + A2 da2 + ..., где A1, A2, ... — функции параметров a1, a2, ... и температуры T, называемые обобщёнными силами[19].

Работу, связанную с изменением количества вещества в системе (химическую работу), могут выделять из общего выражения для работы в отдельное слагаемое

4.Внутренняя энергия и внешняя работа. p-v диаграмма расширения тела.

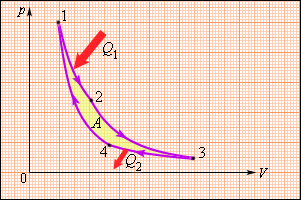
Цикл Карно совершает газ, находящийся в цилиндре под поршнем. На изотермическом участке (1–2) газ приводится в тепловой контакт с горячим тепловым резервуаром (нагревателем), имеющим температуру T1. Газ изотермически расширяется, совершая работу A12, при этом к газу подводится некоторое количество теплоты Q1 = A12. Далее на адиабатическом участке (2–3) газ помещается в адиабатическую оболочку и продолжает расширяться в отсутствие теплообмена. На этом участке газ совершает работу A23 > 0. Температура газа при адиабатическом расширении падает до значения T2. На следующем изотермическом участке (3–4) газ приводится в тепловой контакт с холодным тепловым резервуаром (холодильником) при температуре T2 < T1. Происходит процесс изотермического сжатия. Газ совершает работу A34 < 0 и отдает тепло Q2 < 0, равное произведенной работе A34. Внутренняя энергия газа не изменяется. Наконец, на последнем участке адиабатического сжатия газ вновь помещается в адиабатическую оболочку. При сжатии температура газа повышается до значения T1, газ совершает работу A41 < 0. Полная работа A, совершаемая газом за цикл, равна сумме работ на отдельных участках: A = A12 + A23 + A34 + A41. На диаграмме (p, V) эта работа равна площади цикла.

В соответствии с законом сохранения и превращения энергии количество теплоты, подведенной к телу, соответствует возрастанию его внутренней энергии. Внутренняя энергия тела (U) складывается из энергии поступательного и вращательного движения молекул, составляющих тело, энергии внутримолекулярных колебаний, потенциальной энергии сил сцепления между молекулами, внутримолекулярной энергии, внутриатомной (энергия электронных оболочек атомов) и внутриядерной энергии.

Выше процесс подвода теплоты к телу рассматривался происходящим таким образом, что объем тела сохранялся постоянным. Как известно, в обычных условиях тела при нагревании расширяются. Поэтому в общем случае объем тела при нагревании увеличивается. Если рассматриваемое тело помещено в среду, давление в которой равно рс, то при увеличении объема тела будет совершаться работа против сил внешнего давления рс. В самом деле, рассмотрим процесс увеличения объема V тела произвольной формы, находящегося в среде с давлением Рс. Площадь поверхности тела обозначим F.

Вну́тренняя эне́ргия термодинамической системы (обозначается как E или U) — это сумма энергий теплового движения молекул и межмолекулярных взаимодействий. В аксиоматической термодинамике движение молекул не рассматривается, и внутренняя энергия термодинамической системы определяется как функция состояния системы, приращение которой в любом процессе для адиабатически изолированной системы равно работе внешних сил при переходе системы из начального состояния в конечное

— подведённое к телу количество теплоты, измеренное в джоулях

• — работа, совершаемая телом против внешних сил, измеренная в джоулях

5.Формулировка 1-го закона термодинамики и его математическое выражение.

Первое начало термодинамики выражает универсальный закон сохранения энергии применительно к задачам термодинамики и исключает возможность создания вечного двигателя первого рода, то есть устройства, способного совершать работу без соответствующих затрат энергии.

Внутреннюю энергию U термодинамической системы можно изменить двумя способами, совершая над ней работу или посредством теплообмена с окружающей средой. Первое начало термодинамики утверждает, что теплота, полученная системой, идёт на увеличение внутренней энергии системы и на совершение этой системой работы, что можно записать как δQ = δA + dU. Здесь dU — полный дифференциал внутренней энергии системы, δQ — элементарное количество теплоты, переданное системе, а δA — бесконечно малая или элементарная работа, совершённая системой. Так как работа и теплота не являются функциями состояния, а зависят от способа перехода системы из одного состояния в другое, применяется запись с символом δ, чтобы подчеркнуть, что δQ и δA — это бесконечно малые величины, которые нельзя считать дифференциалами какой-либо функции.

Знаки при δQ и δA в приведённом выше соотношении выражают соглашение о том, что положительной считают работу, совершаемую системой, и теплоту, получаемую системой, принятое в большинстве современных работ по термодинамике.

Если система совершает только механическую работу вследствие изменения её объёма, то элементарная работа записывается как δA = P dV, где dV — приращение объёма. В квазистатических процессах эта работа равна работе внешних сил над системой, взятой с обратным знаком: δAвнутр = –δAвнеш, но для неквазистатических процессов это соотношение не выполняется. В общем случае элементарная работа записывается как сумма δA = A1 da1 + A2 da2 + ..., где A1, A2, ... — функции параметров a1, a2, ... и температуры T, называемые обобщёнными силами[19].

Работу, связанную с изменением количества вещества в системе (химическую работу), могут выделять из общего выражения для работы в отдельное слагаемо

6. Циклы (прямой и обратный). Обратимые и необратимые процессы. Цикл Карно

Циклы прямой и обратный.

Для длительного действия теплового двигателя – машины, непрерывно превращающей теплоту в работу, необходимо непрерывно поддерживать процесс расширения рабочего тела в ее цилиндре или непрерывно периодически повторять процесс расширения в ее цилиндре.

По первому принципу организована работа лопаточных двигателей (турбин), по второму – поршневых двигателей.

Рассмотрим содержание второго принципа, показанного графически на рис. 1. Здесь газ в цилиндре расширяется в процессе 1а2 и совершает работу, равную площади 1а22’1’1. Затем сжимается в процессе 2б1 и возвращается в исходное состояние, точку 1. На сжатие затрачивается работа, равная площади 2б11’2’2. Затем газ опять расширяется по 1а2, сжимается по 2б1 и т.д.

Рис. 1. Прямой цикл Рис.2.Обратный цикл

Замкнутый процесс 1а2б1, в котором газ то расширяется, то подвергается сжатию и проходит через исходное состояние (точку 1), называют круговым процессом или циклом. Цикл, очерченный по часовой стрелке, называют прямым. Площадь прямого цикла выражает полезную работу: lп = lрасшир. – lcжатия = l1a2 – l2б1 = площади 1а2б1. Цикл, очерченный против часовой стрелки, называют обратным (рис. 2). Площадь обратного цикла выражает работу, затраченную на его реализацию.

lз = lcжатия – lрасшир. = l1с2 – l2d1 = площади 1с2d1.

По прямому циклу работают тепловые двигатели, по обратному – холодильные установки.

Эффективность прямых циклов оценивают по величине термического КПД цикла, показывающего, какую долю подведенной теплоты газ превращает в полезную работу. Формула КПД

где q1, q2 – соответственно количество подведенной и отведенной за цикл теплоты.

Характеристикой эффективности обратных циклов является холодильный коэффициент, представляющий собой отношение отведенной от охлаждаемого тела теплоты q2 к затраченной на это работе цикла l3

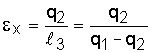
Цикл Карно

Среди всех возможных прямых циклов существует один, имеющий самый высокий термический КПД.

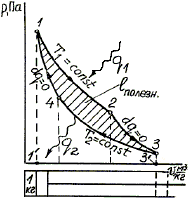
Рис. 3. Прямой цикл Карно

Этот цикл был предложен в 1824 г. французским инженером и ученым Сади Карно. В отличие от прямого цикла (рис. 1), нарисованного произвольно, цикл Карно состоит из конкретных процессов: двух изотерм и двух адиабат (рис. 3). Здесь 1 кг газа расширяется в цилиндре по изотерме 1–2 с подводом теплоты q1, затем по адиабате 2–3, совершая значительную работу (площадь 1233’1’1). Затем газ сжимается по изотерме 3–4 с отводом теплоты q2 и адиабате 4–1, на что затрачивается работа (площадь 3411’3’3).Из точки 1 цикл повторяется.

Найдем термический КПД цикла Карно, учитывая равенство работы и теплоты в изотермическом процессе

где T1, T2 – соответственно температуры теплового источника и теплового приемника (наибольшая и наименьшая температуры в цикле).

Рассмотрев совместно процессы, составляющие цикл Карно, нетрудно показать, что

и КПД определится по формуле:

Цикл Карно называют идеальным, так как он лучше других циклов превращает теплоту q1 в полезную работу. С другой стороны, из-за трудности в организации изотермических процессов он не применяется в реальном двигателе.

Обратимые и необратимые процессы.

Если термодинамическая система под действием внешних сил проходит ряд последовательных состояний, то их совокупность называют термодинамическим процессом. Этот процесс совершается рабочим телом, а его состояние изменяется таким образом, что масса остается постоянной. Основным свойством упрощенного идеального процесса считается его обратимость.

Обратимыми называются процессы, протекающие как в прямом, так и в обратном направлении, и при которых ни в рабочем теле, ни в окружающем пространстве не возникают остаточные изменения. Причем рабочее тело проходит в обоих направлениях через те же самые равновесные элементарные состояния и в конце процесса возвращается в первоначальную точку.

Любой обратимый процесс является равновесным. Процесс называется равновесным, если последовательные состояния, которые проходит система, будут также равновесными. Процесс, протекающий очень медленно и таким образом в любой момент времени приближающийся к равновесному, называется квазистатическим (он также обратим).

Графически равновесное состояние изображается в виде точки в пространственной системе координат с тремя параметрами v, р, Т, а сам равновесный процесс – кривой, проходящей через ряд таких точек.

Состояние системы называется равновесным, если в любой момент времени во всем объеме, который занимает газ, величины v, р, Т (параметры состояния) одинаковы, хотя они изменяются во времени в случае изменения состояния. В случае изолированной системы она со временем возвращается в состояние равновесия и сама из него выйти не может. На практике обратимые процессы возможны при определенных условиях.

1. Рабочее тело изменяет свое состояние бесконечно медленно.

2. У рабочего тела существует бесконечное множество равновесных состояний.

3. Теплообмен с внешней средой (необратимый процесс), внешнее трение, внутреннее трение частиц тела друг о друга отсутствуют.

4. В рабочем веществе не проходят никакие химические изменения.

Процессы, не удовлетворяющие свойству обратимости, являются необратимыми.

Любой реальный процесс, в котором рабочее тело изменяет свое состояние, является необратимым.

Любой реальный процесс является также неравновесным. Это объясняется тем, что процесс имеет конечную скорость и равновесное состояние в рабочем веществе установиться просто не успевает. Реальные процессы могут приближаться к области равновесия, но не совпадать с равновесными процессами, они могут проходить только в прямом направлении, а в обратном – только при воздействии извн

7. Теплоёмкость. Уравнение Майера.

Сообщение телу теплоты вызывает изменение его состояния и в общем случае сопровождается изменением температуры. Было замечено, что для нагрева до одной и той же температуры двух различных тел одинаковой массы и в одинаковых условиях требуется различное количество теплоты. Следовательно, существует какое-то свойство тела, определяющее изменение его температуры в процессе подвода или отвода теплоты. Это свойство называют теплоемкостью тела. Таким образом, теплоемкость тела – это величина, характеризующая способность тела изменять свою температуру с подводом или отводом теплоты. Она равна количеству теплоты, которое надо подвести к телу, чтобы изменить его температуру на 1 К:

, Дж / К,

в дифференциальной форме, т. е. при подводе элементарного количества тепла:

Теплоемкость тела в общем случае не является характеристикой вещества (материала), из которого тело состоит. Она, в частности, будет зависеть от размеров тела. В зависимости от того, в каких единицах измеряется количество вещества – в килограммах, кубометрах,киломолях, различают:

- массовую (удельную) теплоемкость:

т.е. теплоемкость одного килограмма вещества;

- объемную теплоемкость:

т.е. теплоемкость одного кубометра вещества;

- мольную теплоемкость:

т.е. теплоемкость одного киломоля вещества.

Для идеального газа справедливо соотношение Майера:

где ~R — универсальная газовая постоянная,C_p— молярная теплоёмкость при постоянном давлении,C_V— молярная теплоёмкость при постоянном объёме.

Уравнение Майера вытекает из первого начала термодинамики, примененного к изобарному процессу в идеальном газе:

в рассматриваемом случае:

Очевидно, уравнение Майера показывает, что различие теплоёмкостей газа равно работе, совершаемой одним молем идеального газа при изменении его температуры на 1 K, и разъясняет смысл универсальной газовой постоянной R — механический эквивалент теплоты.

8. Идеальный газ. Уравнение состояния идеального газа

Идеальный Газ

Введем ограничения, которые свойственны любой физической теории.

Идеальный газ - модель реального газа, которая удовлетворяет следующим требованиям:

а) Расстояние между молекулами гораздо больше их размеров (молекулы можно считать материальными точками);

б) Силами взаимодействия, кроме моментов соударения, можно пренебречь (потенциальная энергия взаимодействия молекул по сравнению с кинетической энергией хаотического движения пренебрежимо мала);

в) Столкновение молекул друг с другом и со стенками абсолютно упругое;

г) Движение каждой молекулы подчиняется классическим законам динамики Ньютона.

Реальный разреженный газ приблизительно ведет себя как идеальный газ.

Уравнение состояния идеального газа

Взяли порцию газа некоторой массы и начали проводить над ней эксперименты. Например, изменяли некоторый параметр (например, температуру T) и наблюдали, как изменяются другие два параметра (объем V и давление p). При увеличении температуры, молекулы двигаются быстрее, соударения происходят чаще, значит, давление увеличивается и газ стремится занять больший объем. Или, если уменьшить объем, то частицам газа становится тесно, они чаще соударяются, увеличивается давление, а от большого числа соударений их скорость может увеличиваться, то есть может увеличиться температура.

Пришли к зависимости трех макропараметров газа, которую вывел французский физик Б. Клапейрон

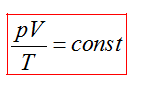
или

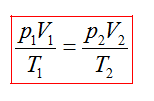
В любом состоянии одной и той же порции газа величинаPV/T остается постоянной.

Д.И. Менделеев исследовал влияние изменения массы газы на макропараметры. Получил зависимость, которое носит название уравнение Менделеева-Клапейрона, оно же уравнение состояния идеального газа