Тема 13. 1. Записать матричное соотношение расчета периодической (циклической) дискретной функции взаимной корреляции последовательностей

Вычислить коэффициенты корреляции, построить график корреляционной функции.

Решение аналогично приведенному в задании 12:

8

7

6

5

4

3

2

1

1 2 3 4 5 6 7 8 9 10

2. Записать матричное соотношение расчета периодической (циклической) дискретной функции взаимной корреляции последовательностей

Вычислить коэффициенты корреляции, построить график корреляционной функции.

Решение аналогично приведенному в задании 12:

14

13

12

11

10

9

8

7

6

5

4

3

2

1

1 2 3 4 5 6 7 8 9 10

3. Записать матричное соотношение расчета периодической (циклической) дискретной функции автокорреляции последовательности Вычислить коэффициенты корреляции, построить график корреляционной функции.

Периодическая автокорреляционная функция последовательности {x(n)} равна:

, где номера отсчётов берутся по модулю N.

Соответствующее матричное представление имеет вид:

Корреляционную функцию можно рассматривать как свёртку, в которой одна из последовательностей обращена во времени, т.е. прочитана в обратном порядке, за исключением нулевого отсчёта.

18

17

16

15

14

13

12

11

10

9

8

7

6

5

4

3

2

1

1 2 3 4 5 6 7 8 9 10

4. Записать матричное соотношение расчета периодической (циклической) дискретной функции автокорреляции последовательности Вычислить коэффициенты корреляции, построить график корреляционной функции.

Периодическая автокорреляционная функция последовательности {x(n)} равна:

, где номера отсчётов берутся по модулю N.

Соответствующее матричное представление имеет вид:

Корреляционную функцию можно рассматривать как свёртку, в которой одна из последовательностей обращена во времени, т.е. прочитана в обратном порядке, за исключением нулевого отсчёта.

10^3

14

13

12

11

10

9

8

7

6

5

4

3

2

1

1 2 3 4 5 6 7 8 9 10

Тема № 14. Алгоритм «разделяй и властвуй». Вычисление полинома в точках с помощью алгоритма «разделяй и властвуй». Привести пример.

Решение:

Алгоритм «разделяй и властвуй»

Разделяй и властвуй (англ. divide and conquer) – важная парадигма разработки алгоритмов, заключающаяся в рекурсивном разбиении решаемой задачи на две или более подзадачи того же типа, но меньшего размера, и комбинировании их решений для получения ответа к исходной задаче. Разбиения выполняются до тех пор, пока все подзадачи не окажутся элементарными.

Умножение двух 2n–значных чисел легкосводится к четырем умножениям n-значных чисел. По методу Карацубы (метод «разделяй и властвуй») достаточно трех таких умножений. Запишем 2n-значное число в виде . Легко проверяется тождество:

Подобным образом можно поступить в случае умножения двух многочленов степени 2n-1 в кольце полиномов над полем Галуа GF(2).

Пусть многочлены p(x) и q(x) степени 2n-1 представлены в виде

где - многочлены степени n-1.

 

Тогда произведение многочленов можно представить в виде

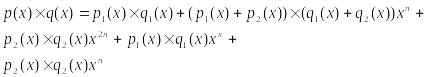(1)

 

Введем обозначения

Тогда формула (1) перепишется в виде

Как видно, использовано только три вместо четырех умножений многочленов степени n. Систематическое применение этого приема соответствует рекурсивной схеме, «разверткой» которой при различных базисах рекурсии можно получить явные схемы умножения, рассматриваемые ниже. Развертка рекурсии производится до того момента, пока не придем к умножению элементарных полиномов.