Тема 5.
1.
Построить
поле порядка
𝐺𝐹(
,
используя
неприводимый над полем
𝐺𝐹(2)
полином
Записать
элементы поля 𝐺𝐹(
через
степенное, векторное и многочленное
представление.
Решение:
Построим конечное поле 𝐺𝐹(2), используя для этого неприводимый полином Поле состоит из всех многочленов степени меньше 3:
0 x x2
1 x+1 x2+1
x2+x
x2+x+1
Сформируем
из полинома 𝑝(𝑥)
= (1+ 𝑥2
+
)
поле Галуа. Элемент поля – это остаток
полученного полинома на 𝑝(𝑥)
= (1+ 𝑥2
+
).
В виде степени |
В виде многочлена |
В виде логарифма |
В виде двоичного вектора |
0 |
0 |
-∞ |
00 |
α0 |
1 |
0 |
01 |
α 1 |
α |
1 |
10 |
α 2 |
α +1 |
2 |
11 |
α3 |
α2 + α |
3 |
100 |
α4 |
α3 + α2 α2 + α + 1 |
4 |
101 |
α5 |
α3 + α2 α2 + α + 1 |
5 |
110 |
α6 |
α3 + α2 + α α + 1 + α2 + α α2 +1 |
6 |
111 |
2.
Привести четыре формы представления
элементов поля Галуа 𝐺𝐹(
).
Поле
образовано многочленами над полем
𝐺𝐹(2)
по
модулю неприводимого многочлена 𝑝(𝑥)
= (1+ 𝑥
+
).
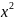Решение:
Приведем четыре формы представления элементов поля Галуа:
В виде степени примитивного элемента |
В виде полинома |
В виде двоичного числа |
В виде логарфма |
- |
0 |
0 0 |
- |
|
1 |
1 0 |
0 |
|
|
0 1 |
1 |
|
1+ |
|
2 |
3.
Привести четыре формы представления
элементов поля Галуа 𝐺𝐹(
).
Поле образовано многочленами над полем
𝐺𝐹(2)
по модулю неприводимого многочлена
𝑝(𝑥)
= (1+
+
).
Решение:
Приведем четыре формы представления элементов Галуа:
В виде степени примитивного элемента |
В виде полинома |
В виде двоичного числа |
В виде логарфма |
0000 |
0 |
0 |
– |
1000 |
1 |
1 |
0 |
0100 |
|
|
1 |
0010 |
2 |
2 |
2 |
0001 |
3 |
3 |
3 |
1100 |
1+ |
4 |
4 |
0110 |
+2 |
5 |
5 |
0011 |
2+3 |
6 |
6 |
1101 |
1++3 |
7 |
7 |
1010 |
1+2 |
8 |
8 |
0101 |
+3 |
9 |
9 |
1110 |
1++2 |
10 |
10 |
0111 |
+2+3 |
11 |
11 |
1111 |
1++2+3 |
12 |
12 |
1011 |
1+2+3 |
13 |
13 |
1001 |
1+3 |
14 |
14 |