Тема 1. 1. Оцените аддитивную, мультипликативную и тотальную сложность вычисления значения полинома :
– при непосредственном вычислении;
– при помощи схемы (алгоритма) Горнера.
Решение:
Непосредственное вычисление:
P(3) = 3*33 + 4*32 + 4*31 + 1= 3*27 + 4*9 + 4*3 + 1 = 81 + 36 + 12 + 1 = 130
Схема Горнера:
Задан многочлен p(x):
X = 3
Представим многочлен p(x) следующим образом:
2.
Оцените аддитивную, мультипликативную
и тотальную сложность вычисления
значения полинома
:
– при непосредственном вычислении;
– при помощи схемы (алгоритма) Горнера.
Решение:
Непосредственное вычисление:
P(3) = 2*34 + 5*33 + 4*32 +4*31 + 1= 2*81 + 5*27 + 4*9 + 4*3 + 1 = 162 + 135 + 36 + 12 + 1 = 346
Схема Горнера:
Задан многочлен p(x):
X = 3
Представим многочлен p(x) следующим образом:
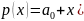
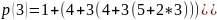
Тема 2. 1. Вычислите множество значений дискретного многочлена Чебышева для
Решение:
для
Т(n)=
0.653 |
0.271 |
-0.271 |
-0.653 |
2.
Вычислите множество значений дискретного
многочлена Чебышева
для
Решение:
для
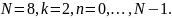
Т(n)=
0.462 |
0.192 |
-0.192 |
-0.462 |
-0.462 |
-0.192 |
0.192 |
0.462 |
Тема
3. 1.а.
Вычислить матричное произведение
𝐴𝐵,
если
𝐴
=
,
𝐵
=
Решение:
1.б.
Вычислите
кронекеровское (прямое) произведение
матриц
𝐴
𝐵,
если
𝐴
=
,
𝐵
=
U=
=
=
=
в. Вычислить значение матрицы 𝑈 = 𝑅 ∨ 𝑆.
U
=
∨
=
Решение:
г. Вычислить значение матрицы 𝐼 = 𝑅 ∧ 𝑆.
𝐼 = ∧ =
д. Вычислить булево произведение матриц
Решение:
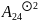
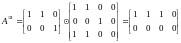
Тема 4.
1. Показать, что группа 𝐺 = < {0,1, 2, 3, 4, 5}; +; 0> содержит подгруппы порядков: 1, 2, 3 и 6.
Решение:
Если g — элемент группы G такой, что gn = 1 для некоторого n, и р — наименьшее положительное целое число такое, что gp = 1, тогда множество {g, g2,..., gp} является подгруппой группы G.
g1=g
g2= g2
g3= g3
g6=1
следовательно, множество {g, g2,..., g6} является подгруппой группы G.
2.
Задана мультипликативная группа <
;
•; 1>. Каков порядок 𝑗? Каков порядок
‒1? Какой элемент может быть использован
в качестве порождающего элемента 𝛼?
Решение:
Порядок элемента j равен 4.
Элемент
(-1) имеет порядок равный 2, т.к.
Порядок элемента (-j) также равен 4. Данная мультипликативная группа является циклической, порожденной элементом j.
3.
Задано множество целых чисел 𝐺 = {1, 2,
3, 4, 5, 6}. Найти функцию Эйлера
.
Решение:
Если а и М взаимно-простые числа, то
,
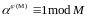где
-
функция Эйлера, равная количеству всех
натуральных чисел, меньших М и
взаимно-простых с М.
В
нашем случае
.
4.
Задана мультипликативная абелева группа
𝐺 = <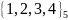
;•;1>.
Построить возможные циклические группы. Определить число примитивных элементов группы.
Решение:
.
Число примитивных элементов равно
.
Примитивным является элемент
Циклическую группу образует множество
Примитивным будет также элемент
Циклическую группу образует множество
5.
Множество
всех четных чисел является подмножеством
целых чисел 𝑍
= {0,
}.
Показать, что < 𝐸;
> ‒ подгруппа группы < Z;
>.
Решение:
Множество всех четных чисел является подмножеством целых чисел Z = {0, }. Тогда < Е; > - подгруппа группы < Z; >.
Представим данные множества:
Z
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
0 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
1 |
1 |
2 |
3 |
4 |
5 |
6 |
0 |
2 |
2 |
3 |
4 |
5 |
6 |
0 |
1 |
3 |
3 |
4 |
5 |
6 |
0 |
1 |
2 |
4 |
4 |
5 |
6 |
0 |
1 |
2 |
3 |
5 |
5 |
6 |
0 |
1 |
2 |
3 |
4 |
6 |
6 |
0 |
1 |
2 |
3 |
4 |
5 |
E
|
0 |
2 |
4 |
6 |
0 |
0 |
2 |
4 |
6 |
2 |
2 |
4 |
6 |
0 |
4 |
4 |
6 |
0 |
2 |
6 |
6 |
0 |
2 |
4 |
Значит
множество Е = {0,
},
является подмножеством целых чисел Z =
{0,
}.