4. Випадкові величини

4.1. Види випадкових величин та способи їх задання

Випадковою величиною називають таку величину, яка внаслідок випробування може прийняти лише одне числове значення, заздалегідь невідоме і обумовлене випадковими причинами.

Випадкові величини звичайно позначають великими літерами , а їх можливі значення – малими літерами з індексами. Наприклад, X – випадкова величина, – її значення, Z – випадкова величина, – її значення.

Випадкові величини бувають дискретними та неперервними.

Означення 1. Дискретною випадковою величиною (ДВВ) називають таку випадкову величину, яка може приймати окремі, ізольовані можливі значення з певними ймовірностями (ці значення можна пронумерувати).

Приклад 1. Якщо X – кількість влучень у мішень при трьох пострілах, то може приймати чотири окремі, ізольовані числові значення 0, 1, 2, 3, 4 з різними ймовірностями. Тому – дискретна випадкова величина.

Якщо – кількість викликів таксі на диспетчерському пункті, то також буде дискретною випадковою величиною, але при значення також зростають, тобто їх кількість прямує до нескінченності. Отже, може приймати значення: .

Означення 2. Неперервною випадковою величиною (НВВ) називають таку випадкову величину, яка може приймати усі значення з деякого скінченного або нескінченного проміжку.

Приклад 2. Величина похибки, яка може виникнути при вимірюванні відстані; час безвідмовної роботи приладу; зріст людини; розміри деталі, яку виготовляє станок-автомат – це неперервні випадкові величини.

Означення 3. Законом розподілу випадкової величини називають таке співвідношення, яке встановлює зв’язок між можливими значеннями випадкової величини і відповідними їм імовірностями.

У випадку дискретної випадкової величини закон розподілу можна задавати таблично, аналітично або графічно.

Табличний спосіб – це ряд розподілу ДВВ

			. . . .		,
			. . . .

де , , . . . – можливі значення ДВВ, записані у порядку зростання ( < < < . . . < ) , , причому .

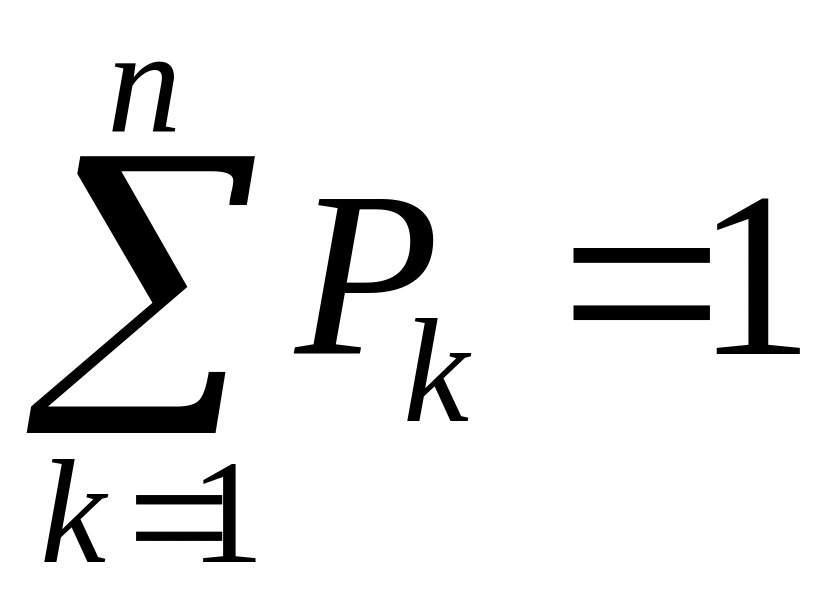Графічний спосіб – многокутник розподілу ДВВ

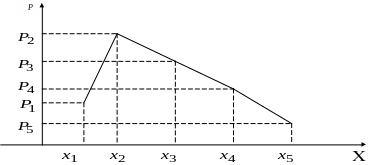
Мал. 3.1.

Аналітичний спосіб задання ДВВ базується на заданні певної функції, за якою можна знайти імовірність відповідного значення , тобто .

У випадку неперервної випадкової величини функціональну залежність задають за допомогою інтегральної або диференціальної функції розподілу.

Означення 4. Функцією розподілу (інтегральною функцією розподілу) називають імовірність того, що випадкова величина прийме значення, менше за :

.

Властивості функції розподілу:

1)

2) – неспадна функція, тобто , якщо ;

3) , ;

4) .

Зауваження. Для неперервної випадкової величини Х, що приймає значення у проміжку ( ) мають місце рівності:

.

Означення 5. Щільністю розподілу ймовірностей f(x) (диференціальною функцією розподілу) неперервної випадкової величини називають похідну першого порядку від її інтегральної функції розподілу:

.

Якщо щільність розподілу ймовірностей відома, то функцію розподілу можна знайти за формулою:

.

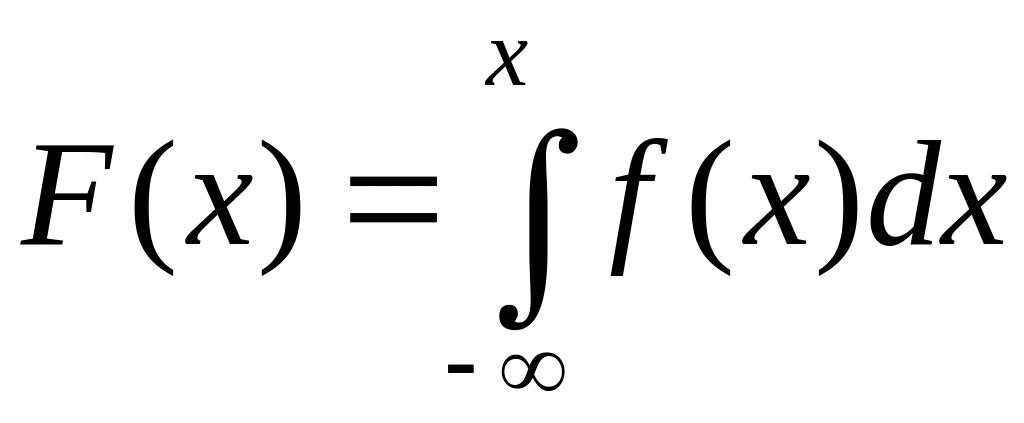Властивості щільності розподілу ймовірностей:

1. ;

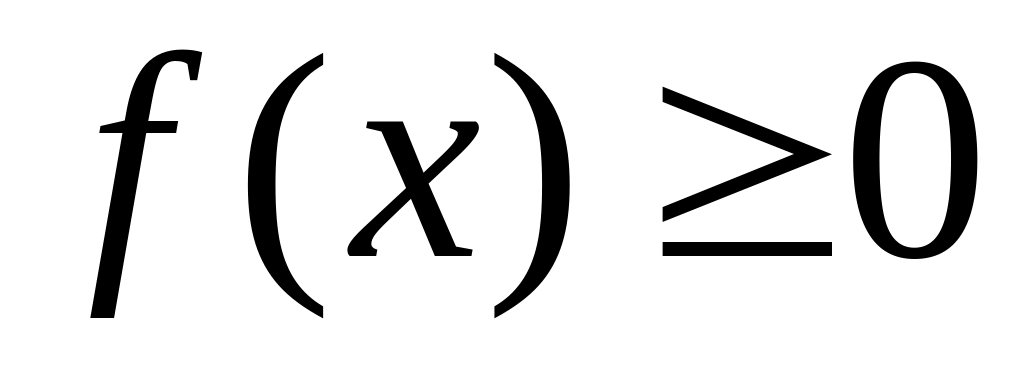2) ;

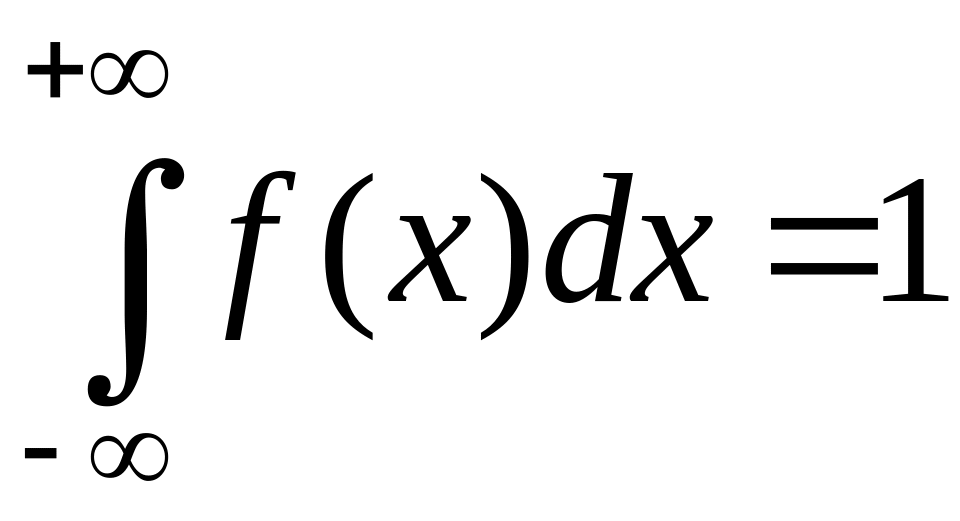3) .

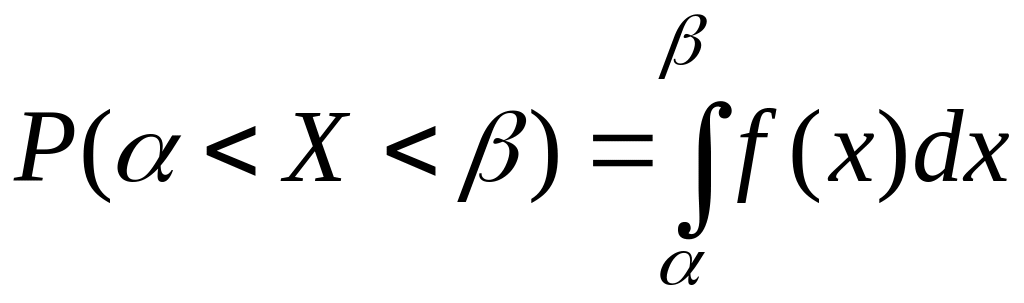Графік щільності розподілу ймовірностей f(x) називають кривою розподілу.