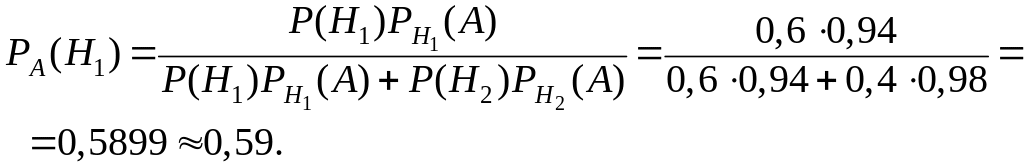2.5. Надійність системи

Означення. Надійністю системи називають імовірність її безвідмовної роботи протягом певного часу (гарантійний термін).

Системи, що складаються з елементів, з’єднаних послідовно:

Мал.2.1.

Системи, що складаються з елементів, з’єднаних паралельно:

Мал.2.2.

При обчисленні надійності системи необхідно виразити її надійність через надійність її елементів (надійність елементів вважається відомою, бо вона пов’язана з технологією їх виготовлення).

Нехай – надійність к-того елемента, – імовірність виходу к-того елемента з ладу протягом часу , – надійність блоку.

Перший випадок – елементи системи з’єднані послідовно (див. мал. 2.1). Система буде працювати безвідмовно, якщо усі елементи працюватимуть безвідмовно.

. (2.3)

Другий випадок – елементи системи з’єднані паралельно (див. мал. 2.2). Система буде працювати безвідмовно, якщо хоча б один елемент не вийде з ладу.

. (2.4)

Зауваження. Будь-яку складну систему можна розглядати як послідовне або паралельне з’єднання блоків, надійність яких обчислюється за формулами (2.3) та (2.4).

Приклад. Імовірності безвідмовної роботи елементів №№ 1, 2, 3, 4, 5, 6, 7 електричної схеми відповідно дорівнюють 0,95, 0,9, 0,85, 0,8, 0,7, 0,6, 0,5. Знайти імовірність проходження сигналу крізь схему

Розв’язання. За умовою задачі ймовірності безвідмовної роботи елементів дорівнюють , , , , , , , а ймовірності відмови елементів відповідно: , , , , , , .

Скориставшись формулами (2.3) та (2.4) можна записати ймовірність безвідмовного проходження сигналу крізь схему:

.

Після підстановки відповідних числових значень, будемо мати:

.

2.6. Формули повної імовірності та Байєса

Припустимо, що

1) подія А може відбутися лише за умови появи однієї з попарно несумісних подій (гіпотез) , які утворюють повну групу, тобто

;

2) відомі умовні ймовірності появи події А при умові появи цих гіпотез .

Тоді ймовірність появи події А обчислюється за формулою повної імовірності:

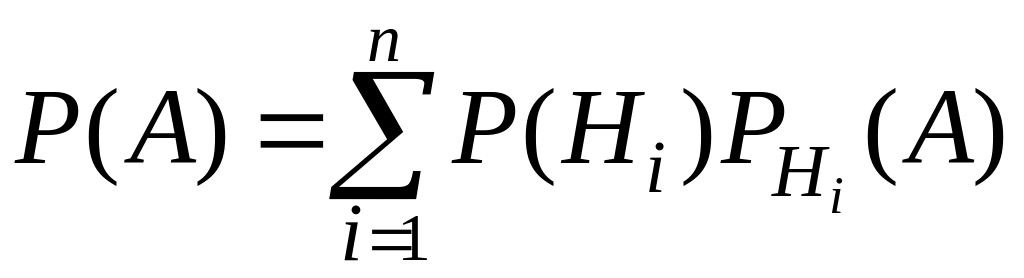. (2.5)

Якщо подія А вже відбулась, то імовірність гіпотез може бути переоцінена за формулою Байєса:

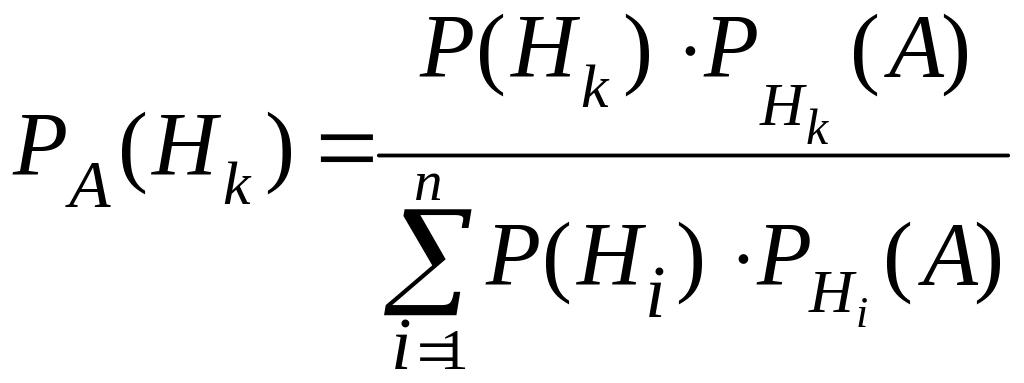. (2.6)

Приклад 1. У першому ящику 20 деталей, серед яких 15 – стандартні. У другому ящику 10 деталей, серед яких 9 – стандартні. З другого ящика беруть навмання одну деталь і перекладають її до першого ящика. Знайти імовірність того, що деталь, яку після цього взято навмання з першого ящика, виявиться стандартною.

Розв’язання. Позначимо такі події: А – з першого ящика взято стандартну деталь; – з другого ящика переклали до першого стандартну деталь; – з другого ящика переклали до першого нестандартну деталь.

Згідно з умовою задачі, з першого ящика можна взяти деталь лише після того, як здійсниться подія або подія .

Події та несумісні, а подія А може з’явитись лише сумісно з однією із них. Тому для знаходження імовірності події А можна використати формулу повної імовірності (2.5), яка у даному випадку набуває вигляду:

Знайдемо потрібні імовірності.

.

(Зауважимо, що , отже, події та утворюють повну групу).

Підставивши ці значення у формулу (2.5), отримаємо:

.

Приклад 2. Деталі, виготовлені цехом заводу, попадають для перевірки їх стандартності до одного з двох контролерів. Імовірність того, що деталь попаде до першого контролера, дорівнює 0,6, а до другого – 0,4. Імовірність того, що придатна деталь буде визнана стандартною першим контролером, дорівнює 0,94, а другим – 0,98. Придатна деталь при перевірці визнана стандартною. Знайти імовірність того, що деталь перевіряв перший контролер.

Розв’язання: Позначимо такі події: А – придатна деталь визнана стандартною; – деталь перевіряв перший контролер; – деталь перевіряв другий контролер.

За умовою прикладу:

.

(Зауважимо, що , отже, події та утворюють повну групу).

За формулою Байєса (2.6) при отримаємо: