4. Основні поняття та принципи комбінаторики

Означення. Різні групи, складені з будь-яких елементів, називають сполуками цих елементів.

Приклад 1. З цифр 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 можна скласти багато різних сполук по 2, 3, 4, … цифр. Деякі з них будуть відрізнятися лише порядком цифр. Наприклад 123, 8056, 96, 312, 231, 321.

Усі можливі сполуки доцільно класифікувати. Сполуки бувають трьох видів:

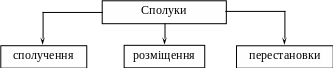
Означення. Сполученнями з n елементів по m називають сполуки, що складаються з m елементів, взятих з даних n елементів , і відрізняються хоча б одним елементом.

Кількість сполучень з n елементів по m позначають і знаходять за формулою

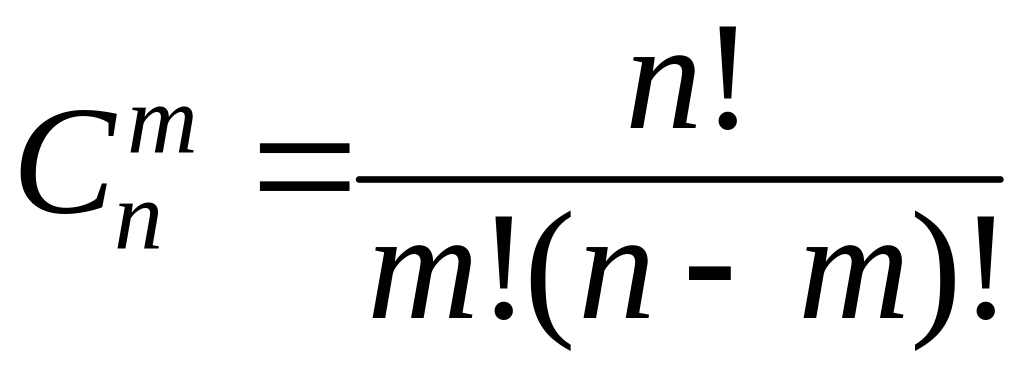. (1.3)

Зауважимо, що за означенням

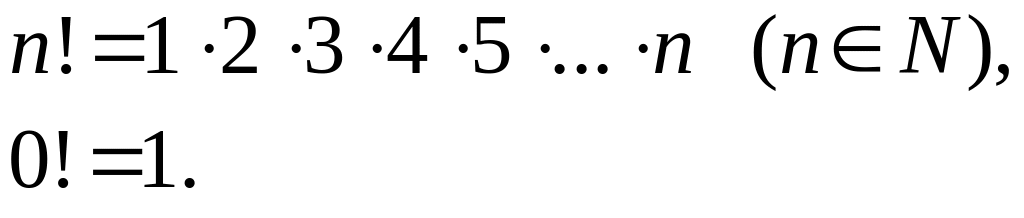
Приклад 2. З 10 кандидатів на одну й ту саму посаду мають бути обрані троє. Скільки існує варіантів вибору?

Розв’язання. Усі можливі варіанти вибору – сполуки з 10 кандидатів по 3, які відрізняються хоча б одним кандидатом, тобто ці сполуки – сполучення. Згідно з формулою (1.3) їх кількість дорівнює

.

Означення. Розміщеннями з n елементів по m називають сполуки, що складаються з m елементів, взятих з даних n елементів , і відрізняються або складом елементів, або порядком їх розташування.

Кількість розміщень з n елементів по m позначають і знаходять за формулою:

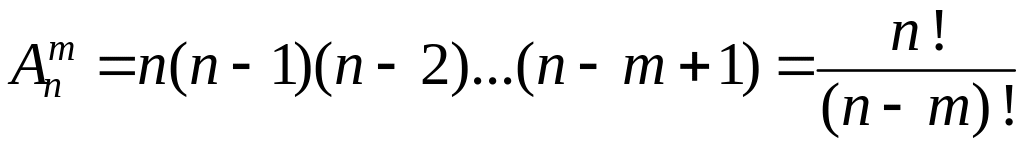. (1.4)

Приклад 3. Студенти другого курсу, згідно з учбовим планом, вивчають 10 дисциплін. На один день можна планувати заняття з 4 дисциплін. Скількома способами можна скласти розклад занять на один день?

Розв’язання. Усі можливі розклади занять на один день – це сполуки з 10 дисциплін по 4, які відрізняються або дисциплінами, або порядком їх розташування, тобто ці сполуки – розміщення. Згідно з формулою (1.4) їх кількість дорівнює

.

Означення. Перестановками з n елементів називають сполуки, що складаються з цих n елементів і відрізняються порядком їх розташування.

Кількість перестановок з n елементів позначають і знаходять за формулою

(1.5)

Приклад 4. Скільки п’ятизначних чисел можна записати, використовуючи п’ять різних цифр (крім нуля)?

Розв’язання. Сполуки, що утворюють з п’яти різних цифр п’ятизначні числа, відрізняються порядком цифр, тобто ці сполуки – перестановки з п’яти елементів. Згідно з формулою (1.5), їх кількість дорівнює

.

Приклад 5. У ящику 10 виробів, з яких 2 нестандартні. Навмання беруть 6 виробів. Яка імовірність того, що усі взяті вироби будуть стандартними?

Розв’язання. Подія А – взято 6 стандартних виробів. Згідно з умовою задачі, немає значення, в якому порядку беруть 6 виробів, отже, це будуть сполучення з 10 виробів по 6. Тому кількість усіх можливих елементарних наслідків буде

.

Події А сприяють лише сполуки по 6 виробів, узятих з 8 стандартних у будь-якому порядку, тобто

.

Отже, згідно з класичним означенням імовірності події А, маємо

.

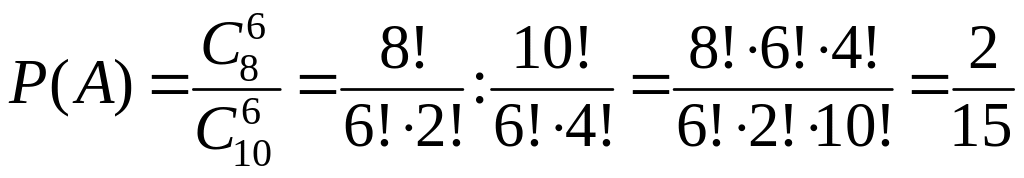Основні принципи комбінаторики

Принцип суми. Якщо множина А містить n елементів, а множина В містить m елементів, і , тоді множина містить n+m елементів.

Принцип добутку. Якщо множина А містить n елементів, а множина В містить m елементів, то множина С усіх можливих пар містить елементів.

Приклад 6. У кошику 4 яблука першого сорту та 5 яблук другого сорту. Навмання беруть 2 яблука. Знайти імовірність того, що ці яблука будуть різних сортів.

Розв’язання. Нехай подія А – навмання взяті 2 яблука різних сортів.

Всього яблук 9, сполучень з них по 2 буде , тобто кількість усіх можливих наслідків .

Події А будуть сприяти сполуки, утворені з пар, елементами яких будуть яблука різних сортів. Згідно з принципом добутку кількість таких пар буде дорівнювати .

Використовуючи класичне означення імовірності, одержимо шукану імовірність події А:

.
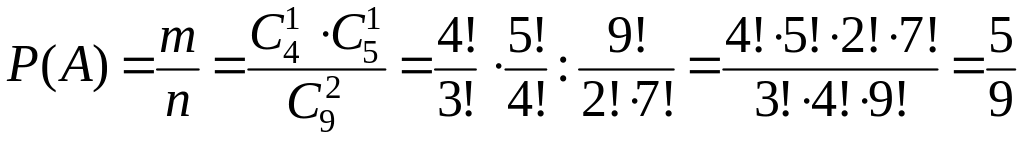