4.4. Основні закони розподілу неперервних випадкових величин

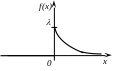
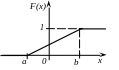
№	Назва закону	Функція щільності ймовірностей f(x) та її графік	Функція розподілу F(x) та її графік	M(X)	D(X)	(X)	P( < X < )
1	Рівномірний розподіл						P( < X <)= = F() – F()
2	Показниковий розподіл	,  >0					P( < X <)= =

Продовження таблиці ___

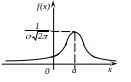
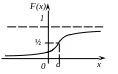
№	Назва закону	Функція щільності ймовірностей f(x) та її графік	Функція розподілу F(x) та її графік	M(X)	D(X)	(X)	P( < X < )
3	Нормальний розподіл		, де	a	2		P( < X < )= = ;
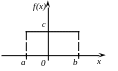
4	Нормований нормальний розподіл ( a = 0,  = 1)		, де – функція Лапласа	0	1	1	P( < X < )= = ;

4.4.1. Нормальний закон розподілу

Неперервна випадкова величина X називається розподіленою за нормальним законом, якщо її щільність розподілу має вигляд

,

де числа a та  – параметри нормального закону розподілу, причому , .

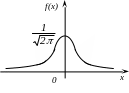
Графік щільності розподілу нормального закону називають нормальною кривою (кривою Гауса)

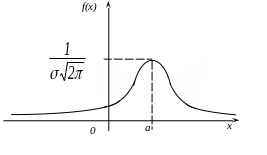
Нормальна крива симетрична відносно вертикальної прямої, яка проходить через точку х = а. Математичне сподівання впливає тільки на місце центра симетрії, тобто на зсув нормальної кривої уздовж осі OX. Зміна  впливає на форму кривої, вона буде тим крутіше, чим менше .

Функція розподілу цієї величини

,

або

,

де 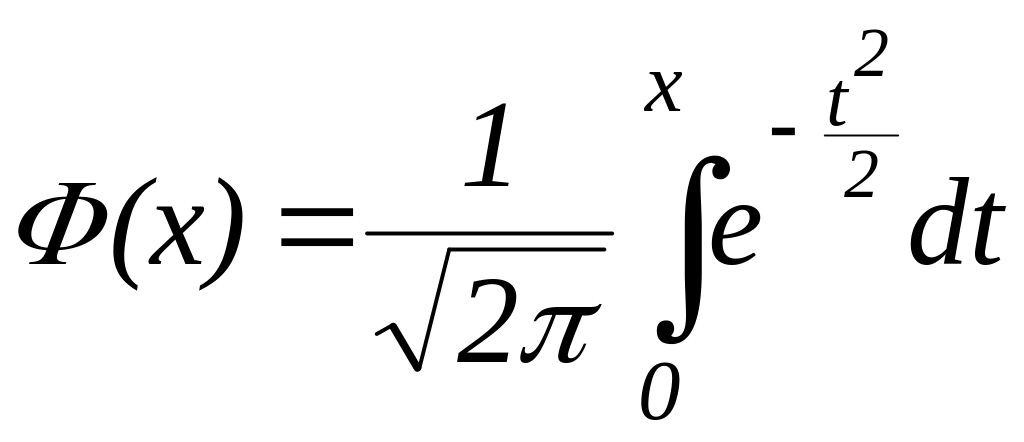– функція Лапласа, або інтеграл імовірності.

Ймовірність того, що нормально розподілена випадкова величина набуде значення з інтервалу (; ), обчислюється за формулою:

,

а ймовірність того, що абсолютна величина відхилення буде менше, ніж додатне число :

.

При отримуємо: . Число 0,997 мало відрізняється від одиниці, тому подію з ймовірністю 0,997 можна вважати достовірною, а останню рівність часто формулюють як «правило трьох сигм»: нормально розподілена випадкова величина Х може відхилятися від свого математичного сподівання не більше, ніж на потроєне середнє квадратичне відхилення.

Нормальний закон розподілу з параметрами а = 0 та  = 1 називається нормованим нормальним законом розподілу.

Приклад 1. Дискретна випадкова величина задана законом розподілу:

X	–2	0	3	5	6
P	0,1	0,2	0,3	0,2	0,2

Необхідно:

1) обчислити математичне сподівання, дисперсію, середнє квадратичне відхилення;

2) побудувати многокутник розподілу;

3) знайти функцію розподілу F(x) і побудувати її графік.

Розв’язання.

1. Обчислимо математичне сподівання за формулою:

.

.

Обчислимо дисперсію за формулою:

.

.

.

.

Обчислимо середнє квадратичне відхилення за формулою:

.

.

2. Побудуємо многокутник розподілу випадкової дискретної величини

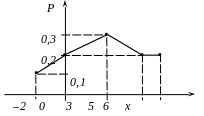
3. Знайдемо функцію розподілу F(x) і побудуємо її графік.

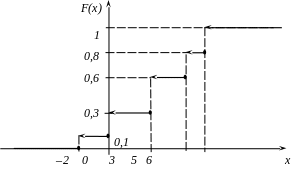
Приклад 2. Задана щільність розподілу ймовірностей неперервної випадкової величини:

Знайти:

1) параметр С;

2) функцію розподілу F(x) та побудувати її графік;

3) імовірність попадання випадкової величини Х в інтервал (–0,5; 0,5).

Розв’язання.

1. Параметр С знайдемо, використовуючи властивість диференціальної функції розподілу:

.

В нашому випадку ця властивість запишеться у вигляді:

, звідки .

Таким чином,

2. Для знаходження функції розподілу F(x) скористаємось формулою:

.

Функція f(x) задана трьома різними виразами на трьох інтервалах. Розглянемо окремо ці інтервали.

Нехай . Тоді .

Нехай . Тоді

.

Нехай .

Тоді

.

Таким чином,

Побудуємо графік функції F(x).

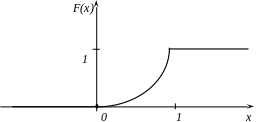
3. Імовірність попадання випадкової величини Х в інтервал 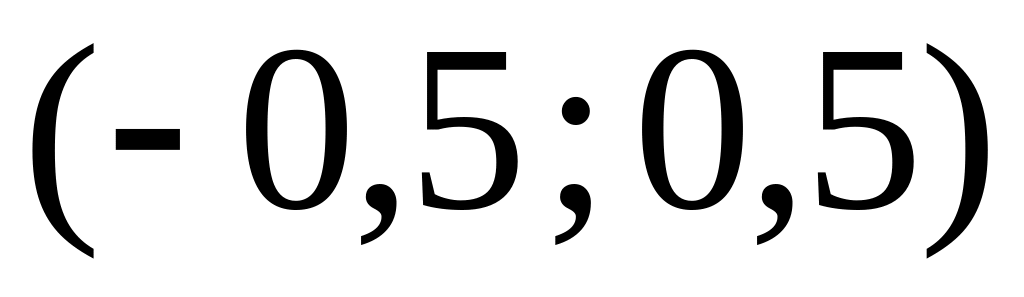можна обчислити двома способами.

Перший спосіб.

Скористаємось властивістю функції F(x):

.

Другий спосіб.

Скористаємось властивістю функції f(x):

В даному випадку отримуємо:

Приклад 3. Неперервна випадкова величина задана функцією розподілу

Знайти:

1) щільність розподілу ймовірностей f(x) та побудувати її графік;

2) математичне сподівання;

3) дисперсію;

4) середнє квадратичне відхилення.

Розв’язання.

1. Щільність розподілу ймовірностей f(x) знайдемо за формулою:

Отже,

Побудуємо графік функції f(x).

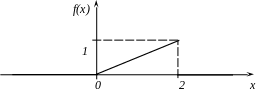
2. Математичне сподівання обчислимо за формулою:

.

У даному випадку:

.

3. Для обчислення дисперсії обчислимо спочатку .

.

Дисперсію обчислимо за формулою: .

.

4. Середнє квадратичне відхилення обчислимо за формулою:

.

.

Приклад 4. Випадкова величина Х розподілена нормально з параметрами та . Знайти імовірність того, що Х відхилиться від свого математичного сподівання по модулю не більше, ніж на 0,2.

Розв’язання. Скористаємось формулою

.

В нашому випадку , , .

Отже, .

Приклад 5. Випадкова величина X розподілена за нормальним законом з параметрами та . Знайти таке значення х, щоб імовірність попадання в інтервал дорівнювала 0,5.

Розв’язання. Імовірність того, що випадкова величина набуде значення з інтервалу , обчислюється за формулою:

.

Підставимо в цю формулу задані значення

.

За умовою задачі . За таблицею .

Тоді .

У таблиці значень функції знайдемо значення , найближче до числа 0,1587. Це число 0,1591. Отже, можна вважати, що . За допомогою вказаних таблиць визначаємо, що , а значить, . Таким чином, отримуємо: .