3.1 Задачи начального уровня
решим несколько примеров. Это один из самых простых типов уравнений, которые будут на ЕГЭ по математике. Но небольшие особенности в выполнении этих заданий есть.
Для решения достаточно провести безошибочно необходимые преобразования, и уметь решать квадратное уравнение. Напомню, что мы можем:
1. Умножать и делить левую и правую части уравнения на одно и то же число или выражение.
2. Прибавлять к обеим частям уравнения или вычитать одно и то же число (выражение).
По-другому эта операция звучит так: перенос слагаемых, из левой части в правую и наоборот, при этом знак слагаемого изменяется на противоположный.
3. Можем возводить в квадрат и извлекать квадратный корень из обеих частей.
Квадратное уравнение (общий вид):
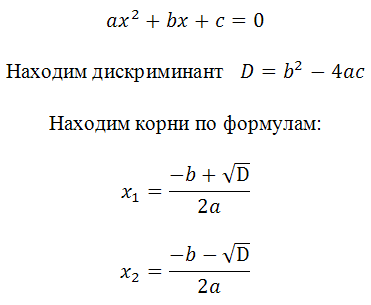
И главное. Обязательно делайте проверку после того как найдёте корни. В некоторых примерах вы получите два корня и вам будет нужно выбрать один из них. Так вот – проверку делайте для обоих корней, а затем выбирайте указанный в условии корень. Только в этом случае ошибка будет практически исключена. Решим примеры:
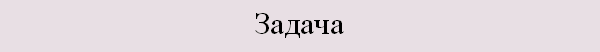
Найдите корень уравнения:
Отметим, что х не равен пяти (обращает знаменатель в ноль). Умножим обе части уравнения на (х – 5):
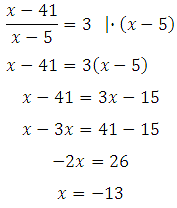
Сделаем проверку:
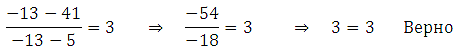
Ответ: –13
Найдите
корень уравнения:
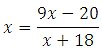
Если уравнение имеет более одного корня, в ответе укажите больший из них.
Сразу отметим, что х ≠ 18, так как при х = – 18 знаменатель обращается в ноль, а на ноль делить нельзя. Умножим обе части на (х+18):
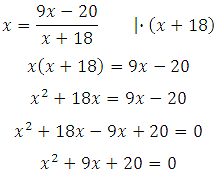
Решаем квадратное уравнение:
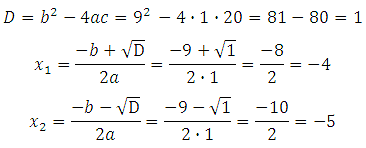
Больший из них – 4.
Сделаем проверку (проверяем оба корня):
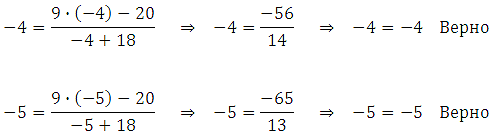
Ответ: – 4
Решите уравнение:
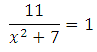
Если уравнение имеет более одного корня, в ответе запишите меньший из корней.
Умножим обе части на (х2 + 7), получим:
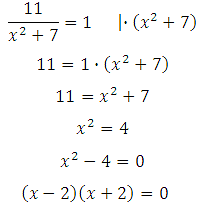
Разложили как разность квадратов.
Произведение равно нулю тогда, когда хотя бы один из множителей равен нулю, значит
х – 2 = 0 или х + 2 = 0
х1 = 2 х2 = – 2
Меньший из корней равен –2.
Сделаем проверку:
Второй корень в данном случае можно не проверять.
Отмечу, что корни уравнения х2 = 4 можно было записать сразу. Но я намеренно сделал разложение, так как это будет математически более грамотно. Разумеется, на самом ЕГЭ этого можно не делать.
Ответ: –2
Решите уравнение:
Если уравнение имеет более одного корня, в ответе запишите больший из корней.
Так как результат дроби равен 1, то можем записать, что числитель равен знаменателю:
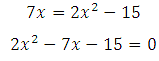
Решаем квадратное уравнение:
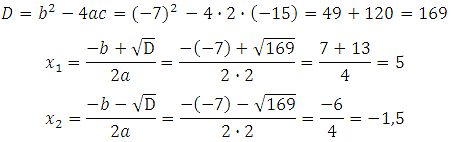
Больший из корней равен 5.
Сделаем проверку (проверяем оба корня):
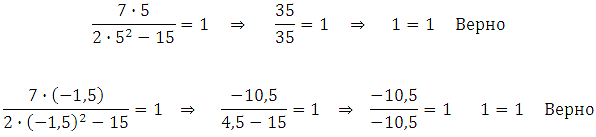
Ответ: 5
Решите
уравнение:
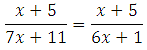
Если уравнение имеет более одного корня, в ответе запишите больший из корней.
Умножим обе части на (7х + 11)(6х + 1), получим:
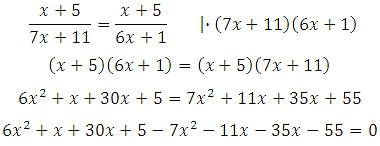
Сокращаем подобные члены, получим – х2 – 15х – 50 = 0
Умножаем обе части на –1:
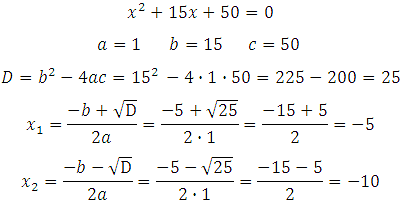
Больший из корней равен – 5.
Проверка (проверяем оба корня):
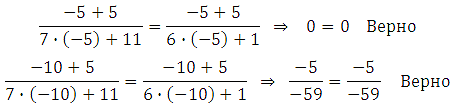
Ответ: – 5
Найдите корень уравнения:
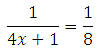
Сразу же можно воспользоваться следующим свойством: числители дробей равны, поэтому без лишних преобразований сразу можем приравнять их знаменатели:
4х + 1 = 8
4х = 7
х = 1,75
Сделаем проверку:
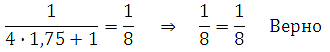
В данном примере можно было воспользоваться и обычными преобразованиями, умножить обе части уравнения на 8 (4х + 1).
Ответ: 1,75