4. Переходные процессы в цепи с последовательно соединенными r, l и с (контуры II порядка)

Уравнение цепи, представленной на рис 1.13, выглядит следующим образом:

, (1.22)

Продифференцируем уравнение (1.22)

. (1.23)

Решение ищем в виде:

_{. (1.24)}

Запишем уравнение (1.23) для свободной составляющей:

.

Введем обозначения , - коэффициент затухания, , - частота свободных колебаний.

Запишем характеристическое уравнение:

.

Корни характеристического уравнения равны:

.

Свободную составляющую ищем в виде

.

Тогда формула для тока приводится к следующему виду

. (1.23)

А₁ и А₂ находятся из условий неизменности тока в катушке и напряжения на конденсаторе в момент коммутации:

, .

Для определения А₁ и А₂ надо знать величину тока и его производных до порядка включительно при t=0. В данном случае , поэтому достаточно знать начальное значение тока и его первой производной. Начальная величина тока известна.

Начальную величину производной тока находим из исходного уравнения

. (1.24)

Отсюда находим

.

Из (1.23) имеем

. (1.25)

Из (1.23) и (1.25) при t=0 имеем

(1.26)

где есть значения установившегося тока и его производной в начальный момент времени, известные из найденного ранее частного решения исходного дифференциального уравнения (1.22). Из системы уравнений (1.26) находим А₁ и А₂.

1.5. Разряд конденсатора на цепь r и l

Пусть t=0 есть момент коммутации.

До коммутации напряжение на конденсаторе равно , ток через индуктивность равен .

Согласно законам коммутации запишем начальные условия

, .

З апишем уравнение цепи после коммутации, учитывая, что приложенное напряжение отсутствует ( ):

.

Решение ищем в виде . Учтем, что установившийся ток равен нулю и из-за наличия индуктивности .

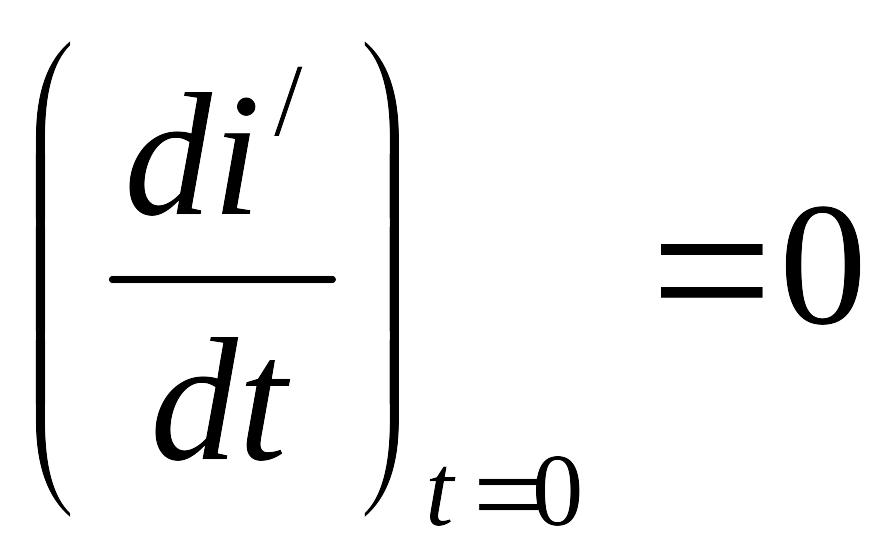Тогда переходный ток равен:

. (1.27)

При из (1.26) имеем:

.

Отсюда находим постоянные:

.

Подставим А₁ и А₂ в формулу (1.27) и получим:

.

Найдем напряжение на индуктивности: _.

Напряжение на конденсаторе равно:

,

так как , то .

Характер процесса разряда существенно зависит от корней характеристического уравнения, т.е. от параметров цепи.

А). Апериодический разряд.

К орни характеристического уравнения вещественные и отличные по величине. Для этого должно выполняться условие или отсюда . При этом условии - , . Для определенности допустим, что , поэтому при . Это показано на рис. 1.15.

М ожно видеть, что ток i не меняет своего направления (i<0, U>0), т.е. конденсатор все время разряжается. Такой односторонний разряд конденсатора называется апериодическим. На рис. 1.16 показаны графики этого разряда.

В этом случае имеем два характерных интервала разряда, разделенных точкой , при которой ток достигает максимума. При и имеют разные знаки т.е. конденсатор отдает энергию резистору (R) и катушке

При имеем т.е. в резистор поступает энергия от конденсатора и катушки.

Б) Критический режим (предельный случай апериодического разряда).

В этом режиме корни характеристического уравнения вещественны и равны друг другу. Соблюдается условие , т.е. . В этом случае . Формулы для тока и напряжения носят неопределенный характер. Имеется неопределенность типа Раскроем неопределенность по правилу Лапиталя, полагая переменной, стремящейся к Тогда выражение для тока записывается следующим образом:

.

Найдем напряжение на индуктивности:

.

Найдем напряжение на конденсаторе:

.

В этом режиме характер процесса разряда такой же, что и при . Случай - предельный (пограничный), т.к. при разряд становится колебательным.

Критический режим предполагает быстрое спадание амплитуды без колебаний и наиболее желателен во всех индикаторных, измерительных и контрольных приборах.

В) Колебательный разряд.

В колебательном режиме корни характеристического уравнения - комплексные сопряженные числа. Это получается, когда выполняется условие , т.е. .

Обозначим . Тогда корни равны:

.

Здесь . Следовательно .

Ток равен:

,

.

Напряжение на катушке равно:

Напряжение на конденсаторе равно:

Графики приведены на рис. 1.17.

Как можно видеть разряд носит колебательный характер. Кривые тока и напряжения периодически меняют знак. Данные величины колеблются с угловой частотой и периодом . Как можно заметить затухание влияет на частоту колебаний, но это эффект второго порядка, поэтому в большинстве случаев этим влиянием пренебрегают.

Амплитуда колебаний уменьшается согласно экспоненте, другими словами: колебания затухают. Интенсивность затухания характеризуется декрементом колебаний , равным отношению двух соседних максимумов одного знака:

или логарифмическим декрементом колебаний .

На графике выделим характерные точки:

• (ток достигает максимума, );

• ( );

• ( ).

В интервале конденсатор разряжается на R и L.

В интервале в R поступает энергия от конденсатора и катушки.

В интервале конденсатор заряжается за счет энергии магнитного поля катушки.

Описанный процесс, происходящий при повторяется и в следующем полупериоде, но знаки тока и напряжений противоположны соответствующим знакам в первом полупериоде, а сами эти величины становятся меньше из-за потерь, выделяющихся на R.

В предельном случае (R=0) имеем В этом случае колебания не затухают и имеют период (формула Томсона). При этом угловая частота колебаний равна резонансной частоте контура.