8 .5. Дуальные цепи.
Если сопоставить резонансные кривые и выражения для последовательного и параллельного контуров, то зависимости полностью совпадут, если заменить ток (I) на напряжение (U), емкость (C) на индуктивность (L), сопротивление (R) на проводимость (G). Такие цепи называются дуальными.
Д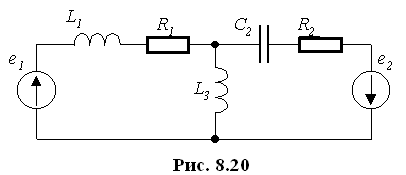
уальными
цепями являются две любые электрические
цепи, в которых взаимно соответствуют:
контурам – узлы; последовательное
соединение – параллельному соединению;
источникам ЭДС (E)
– источники тока (J);
индуктивностям (L)
– емкости (C);
сопротивлениям (R)
– проводимости (G).
Процессы в дуальных цепях аналогичны, если заменить U на I и обратно, т.е. резонансу U в одной схеме соответствует резонанс I в другой схеме.
С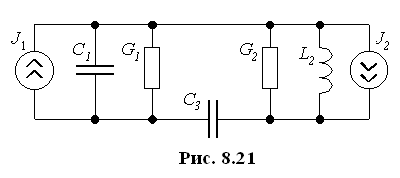
хеме
на рис. 8.20 соответствует дуальная схема
на рис. 8.21.
Свойства дуальных цепей:
Равенству
соответствует.
.Преобразование “звезда-треугольник” соответствует преобразованию “треугольник-звезда”.
3) Исключение контура (узла) соответствует исключению узла (контура)
4)
Если численно выполняется равенство
и
,
то соответственно численно
выполняются следующие равенства i=u
и u=i.
9. Четырехполюсники
Электротехнические устройства, имеющие два входных и два выходных зажима, называются четырехполюсниками. Четырехполюсники, имеющие внутри источники энергии, называются активными, если таких источников нет – то они называются пассивными. Активный четырехполюсник можно представить в виде эквивалентного пассивного с вынесенными на зажимы эквивалентными ЭДС. Поэтому рассмотрим пассивные четырехполюсники. Примерами таких четырехполюсников являются: трансформатор, линия электропередачи, электрический фильтр и др.
9.1.Основные соотношения четырехполюсника
Р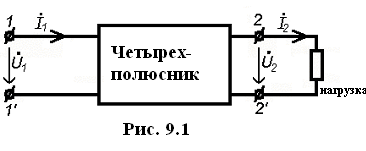
ассмотрим
синусоидальный режим четырехполюсника.
Выберем положительные направления
токов и напряжений.
Допустим,
что четырехполюсник содержит
независимых контуров (рис. 9.1). Поставим
задачу связать входные величины (
и
)
с выходными величинами (
и
).
В качестве первого выберем контур,
включающий источник энергии, присоединенный
к выходным зажимам 1, 1/.
В качестве второго – контур, содержащий
приемник, подключенный к выходным
зажимам 2, 2/.
Составим уравнения по методу контурных токов. Собственные и общие сопротивления контуров внутри четырехполюсника снабдим штрихом (/).
,
…………………………………………..
.
О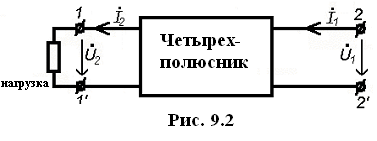
тсюда
найдем токи
=
,
=
,
где Δij
- адъюнкта элемента
.
Дроби при напряжениях имеют размерность
проводимости, поэтому обозначим:
, -
,
, -
.
Для
линейных четырехполюсников
,
поэтому
.
Тогда уравнения четырехполюсников получат вид:
,
(9.1)
или в матричной форме:
=
,
=
,
=
,
где
- матрица проводимости.
Так
как
, то
– симметричная матрица.
(9.1) - первая форма записи уравнений четырехполюсника. Записывая эти уравнения относительно напряжений, получим вторую форму записи уравнений:
,
(9.2)
или в матричной форме:
,
=
- матрица
сопротивлений,
где
11
=
,
22
=
,
12
=
,
21
=
.
Т.к.
,
то
.
Наибольшее
распространение получили уравнения
четырехполюсника в форме записи, при
которой входные величины
и
выражаются через выходные
и
,
(9.3)
или
в матричной форме:
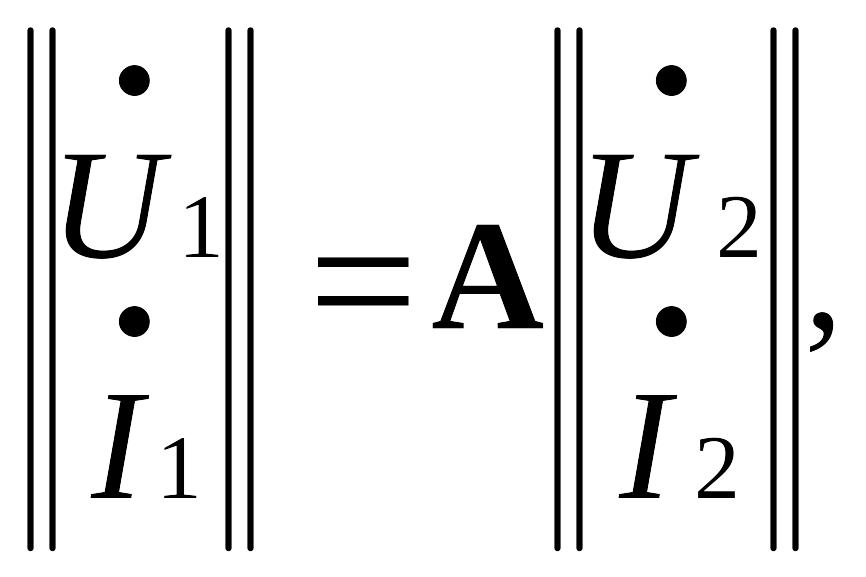
- цепочная
матрица,
=
,
,
,
= -
.
и
имеют нулевую размерность;
имеет размерность сопротивления,
имеет размерность проводимости.
Так
как
,
то
.
Эта связь, а также соотношения
и
показывают, что независимо от формы
записи уравнений четырехполюсника,
независимыми являются три
параметра.
Это значит, что при синусоидальном
режиме свойства четырехполюсника
определяются тремя параметрами.
Если поменять местами входные и выходные зажимы, то получим схему (на рис. 9.2).
Сравнивая
рис. 9.1 и рис. 9.2, видим, что поменялись
местами напряжения
и
c сохранением знака и токи
и
- с переменой знака. Сделаем эту замену
в уравнениях (9.3). Получим
2
=
1
+
,
=
1
-
.
Отсюда, учитывая , получим:
1
=
2+
,
=
2
+
.
(9.4)
Таким образом, при замене местами входных и выходных зажимов в уравнениях четырехполюсника меняются местами величины и .
Если
свойства четырехполюсника одинаковы
со стороны входных и выходных зажимов,
то
.
Такие четырехполюсники называются
симметричными.
Для них независимыми являются только
два параметра.
При принятых на рис. 9.1 и рис. 9.2 положительных направлениях напряжений и токов энергия от источника поступает в четырехполюсник, а от четырехполюсника она поступает к нагрузке. Иногда можно встретить уравнения четырехполюсника, полученные в предположении, что энергия поступает в четырехполюсник как со стороны входных, так и со стороны выходных зажимов. Это значит, что положительное направление тока изменяется на обратное, так что схема четырехполюсника представляется в виде, показанном на рис. 9.3.
Уравнения
для этой схемы получим из вышеприведенных
уравнений (9.1), изменив знак перед
.
Однако, чтобы сохранить принятую запись
уравнений и для этой схемы, надо положить:
, - , , - .
В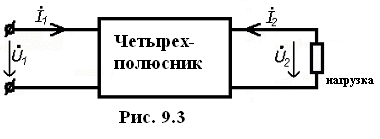
уравнениях
1+
2
,
1+
2
заметим, что
,
так как
.
Таким образом, по сравнению с предыдущим
случаем изменим знак у параметров
и
.
Это приводит к тому, что: 1) изменится
знак у
,
2) к равенству
,
3) к уравнению
.
В заключение отметим, что безразлично как задавать положительное направление тока .