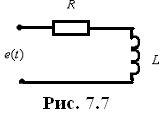
Ток в цепи и напряжение на индуктивности равны

сходится медленнее, чем . Улучшить сходимость можно методом Ланцоша.

Тогда ЭДС записывается следующим образом г де .

Допустим, что . Коэффициенты Ланцоша вычисляются следующим образом

В результате получим

7.2. Расчет токов в линейной цепи при действии периодического несинусоидальные эдс или напряжения.

1) Пусть в линейной цепи действуют несинусоидальные ЭДС либо несинусоидальные напряжения (рис. 7.9). Эти величины раскладываем в ряд Фурье (рис. 7.10)

Н ужно найти ток. Так как цепь линейная, то можно утверждать, что каждая гармоника ЭДС (или напряжения) вызовет соответствующую гармонику тока. Например, постоянная составляющая ЭДС (напр.) - постоянную составляющую тока, k-ая гармоника ЭДС (напр.) – k-ую гармонику тока и т.д. Т.о. ток в цепи согласно принципу суперпозиции будет равен .

При этом расчет для каждой гармоники производится независимо от других гармоник. Нужно помнить, что R=const, .

2). Пусть в линейной цепи действуют источники несинусоидального тока (рис. 7.11). Эти величины раскладываем в ряд Фурье (рис. 7.10) (рис. 7.12).

Нужно найти напряжение. Рассуждаем по аналогии с предыдущим случаем. Напряжение цепи согласно принципу суперпозиции будет равно .

Если периодическая несинусоидальная функция f(t) удовлетворяет условию или (сюда относится также функции, приобретающие указанное свойство при соответствующем сдвиге их по оси t), то f(t) характеризуется тремя коэффициентами: коэффициентом формы k_ф, коэффициентом амплитуды k_а и коэффициентом искажения k_и.

.

Здесь - максимальное значение функции; F - действующее значение функции; - среднее значение; - действующее значение основной гармоники.

Пример

Р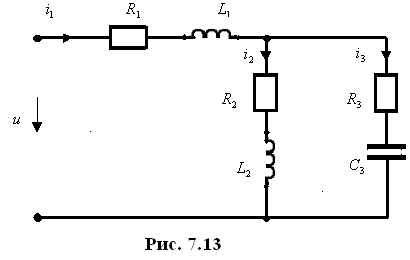 ассмотрим цепь (рис. 7.13). Она подключена к периодическому несинусоидальному напряжению , где

Постоянная составляющая равна . Все другие составляющие тока находятся комплексным методом, для чего представим отдельные гармоники напряжения в комплексной форме

Достаточно произвести расчет для одной гармоники, например . Тогда, полагая в формуле для гармоники тока, получим первую гармонику и т.д.

Для гармоники имеем схему, показанную на рис. 7.14.

Сопротивления равны

(7.5)

Составим уравнения по законам Кирхгофа и найдем токи в ветвях

(7.6)

П олагая в (7.5) и (7.6) , получаем первую гармонику тока и т.д.

Чему же будут равны токи в ветвях? Складывать гармоники, выраженные в комплексной форме, нельзя, т.к. они имеют разные частоты. Можно складывать лишь мгновенные значения тока, т.е. гармоники, выраженные в тригонометрической форме. Так что токи в ветвях будут равны

где

Находим напряжения на реактивных элементах по формулам

7.3. Зависимость формы кривой тока от параметров цепи при несинусоидальном напряжении

Ток в линейной цепи при заданном напряжении определяется ее параметрами: активным сопротивлением ( ), индуктивным сопротивлением катушки ( ) емкостным сопротивлением ( ). Если пренебречь поверхностным эффектом, то можно считать не зависящим от . Суть поверхностного эффекта состоит в следующем. Переменный ток при протекании по проводнику создает магнитное поле вокруг проводника и в теле проводника. Это поле изменяется во времени и в проводнике индуктируется ЭДС, которая создает так называемый вихревой ток. Согласно правилу Ленца вихревой ток направлен против рабочего тока. Вихревой ток проходит в основном вдоль оси проводника и вблизи этой оси. Поэтому центральная часть провода оказывается разгруженной от тока, ток проходит в основном по периферии проводника. Это явление известное как поверхностный эффект, уменьшает эффективное сечение провода, что приводит к увеличению его сопротивлению. Поверхностный эффект проявляется тем сильнее, чем больше сечение провода и частота тока. Мы поверхностный эффект не учитываем, поэтому будем считать .

Индуктивное сопротивление катушки прямо пропорционально частоте

Емкостное сопротивление обратно пропорционально частоте

Т.о., если к цепи приложено несинусоидальное напряжение , то кривая тока будет подобна кривой , если в этой цепи содержится (поверхностный эффект не учитывается). В этом случае для всех и поэтому .

Если в цепи имеется индуктивная катушка и конденсатор, то кривая тока по форме будет отличаться от кривой напряжения.

Пусть в цепи имеется только , тогда

отсюда

Т.е. высшие гармоники в кривой тока проявляются в меньшей степени, чем в кривой напряжения. Катушка индуктивности сглаживает кривую тока. Это явление применяется в выпрямителях.

Пусть имеется в цепи только , тогда

, ,

Т.е. высшие гармоники в кривой тока проявляются сильнее, чем в кривой напряжения.

К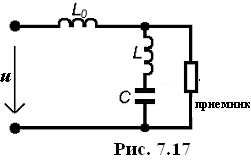 онденсатор искажает кривую тока по сравнению с кривой напряжения. В случае сложной цепи, содержащей сопротивление , индуктивные катушки и конденсаторы, на форму кривой тока будет влиять конфигурация цепи.

П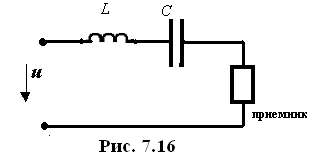 усть требуется преимущественное прохождение гармоники в приемник (рис. 7.16). Очевидно надо подобрать и так, чтобы При этом . Т.о. для указанной гармоники нужно создать резонанс напряжения.

Пусть требуется, чтобы гармоники тока не было в приемнике. Для этого нужно построить цепь (рис. 7.17) и подобрать и так, чтобы . Тогда k-ая гармоника пройдет по ветви из L и C. Если напряжение содержит постоянную составляющую, то соответствующий ей постоянный ток пойдет только в приемник, т.к. сопротивление конденсатора для постоянного тока бесконечно, а индуктивное сопротивление катушки L₀ равно нулю. Такой метод широко используется на выпрямительных устройствах подстанций, питающих контактную сеть электрических железных дорог. Напряжение выпрямителей содержит, кроме постоянной составляющей, ряд гармоник. Тогда поступают следующим образом: после выпрямителя и L₀ включают ветви из L и С, настраивая эти ветви в резонанс на частоты гармоник, которые не хотят допустить в контактную сеть (рис. 7.18).

Е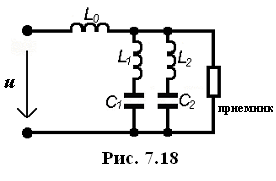 сли в цепи для гармоники имеет место резонанс токов, то сопротивление цепи этой гармоники максимально и эта гармоника в кривой тока будет ослаблена. Примером такой цепи является схема на рис. 7.19, где L и С подбираются так, чтобы их проводимости были равны. . Тогда .

Электрические цепи, предназначенные для преимущественного пропуска или задержки токов определенных частот, называется фильтрами. Здесь были приведены примеры простейших фильтров.