
- •Часть 3 Учебное пособие
- •6.5. Использование метода симметричных составляющих для расчета трехфазных цепей
- •7. Линейные электрические цепи несинусоидального тока
- •7.1. Ряды Фурье.
- •Ток в цепи и напряжение на индуктивности равны
- •7.2. Расчет токов в линейной цепи при действии периодического несинусоидальные эдс или напряжения.
- •7.3. Зависимость формы кривой тока от параметров цепи при несинусоидальном напряжении
- •7.4. Действующие значения периодических несинусоидальных величин
- •7.5. Активная мощность периодических несинусоидальных напряжений и токов
- •7.6. Особенности поведения высших гармоник в трехфазных цепях.
- •7.7. Биения колебаний.
- •7.8. Модулирование колебаний.
- •8. Резонансные явления в электрических цепях и частотные характеристики
- •9.1. Последовательный колебательный контур. Резонанс напряжений
- •8.2. Частотные характеристики последовательного r‑l‑c контура.
- •8.3. Параллельный колебательный контур. Резонанс токов
- •8.4. Частотные характеристики параллельного r‑l‑c контура.
- •8 .5. Дуальные цепи.
- •9. Четырехполюсники
- •9.1.Основные соотношения четырехполюсника
- •9 .2. Эквивалентные схемы четырехполюсника
- •9.3. Экспериментальное определение параметров двухполюсника
- •9.4. Активный четырехполюсник
- •9.5. Дифференцирующие и интегрирующие цепи
- •9.6. Цепные схемы
- •Домашняя работа «Расчет цепи постоянного тока»
- •2. Расчет токов в ветвях цепи методом контурных токов.
- •3. Определение показаний вольтметров
- •4. Проверка баланса мощностей.
- •5. Расчет потенциалов в точках соединения элементов внешнего контура и построение потенциальной
- •6. Расчет тока в сопротивлении r1 методом эквивалентного
- •7. Расчет тока в сопротивлении r1 методом эквивалентного
- •Домашнее задание “Расчет цепи синусоидального тока комплексным методом”
ПЕТЕРБУРГСКИЙ
Г ОСУДАРСТВЕННЫЙ
УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ
ОСУДАРСТВЕННЫЙ
УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ
K.K. Kим
САМОУЧИТЕЛЬ ПО ТЕОРИИ ЛИНЕЙНЫХ
ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ
Часть 3 Учебное пособие
Санкт-Петербург
2005
УДК 621.3.01
ББК 31.211
Kим K.K.
Самоучитель по теории линейных электрических цепей. Ч.3: Учебное пособие . – СПб.: Петербургский государственный университет путей сообщения, 2005. – 60 с.
Библ.: 19. Fig. 86.
Основные проблемы теории и расчета линейных электрических цепей рассмотрены в данном пособии.
Учебное пособие написано в соответствии с дисциплиной «Теоретические основы электротехники» и является продолжением учебных пособий К.К. Кима «Самоучитель по теории линейных электрических цепей», ч.1, ч.2. Поэтому нумерация рисунков и формул выполнена в соответствии с нумерацией предыдущих пособий. Пособие предназначено для студентов-заочников электромеханических и электротехнических специальностей.
Пособие может быть полезно инженерам и аспирантам.
K.K. Kим, 2005
В голове мотив один, чемпион – «Локомотив»!!!
Народная железнодорожная мудрость
6.5. Использование метода симметричных составляющих для расчета трехфазных цепей
Несимметричным
режимом трехфазных цепей называется
режим, при котором как напряжения, так
и токи образуют несимметричную систему.
При расчете несимметричного режима в
линейных трехфазных цепях применяют
метод симметричных составляющих.
Особенно этот метод эффективен в тех
случаях, когда трехфазное устройство
имеет разные сопротивления для токов
разных последовательностей. Примером
таких устройств является трехфазная
электрическая машина, в которой
используется вращающее магнитное
поле.
Если сопротивления такой машины
при протекании в ней токов нулевой,
прямой и обратной последовательности
соответственно обозначить через
![]() ,
,
![]() и
и
![]() ,
то
,
то
![]()
![]() .
Для каждой из последовательностей
машина симметрична. Так, для токов
нулевой последовательности сопротивление
всех трех фаз одно и тоже и равно
.
Для каждой из последовательностей
машина симметрична. Так, для токов
нулевой последовательности сопротивление
всех трех фаз одно и тоже и равно
![]() ,
для токов прямой последовательности
сопротивление каждой фазы равно
,
для токов прямой последовательности
сопротивление каждой фазы равно
![]() и т.д.
и т.д.
Суть метода симметричных составляющих применительно к трехфазным цепям, которые симметричны для каждой последовательности токов, состоит в следующем: токи каждой последовательности определяются только ЭДС и напряжениями той же последовательности. Поэтому расчет для каждой последовательности можно сделать независимо.
Рассмотрим
случай однофазного замыкания генератора
на землю (рис. 6.17). Обмотки генератора
соединены в звезду, нейтральная точка
генератора соединена с землей через
сопротивление
![]() .
Генератор симметричен и, следовательно,
его ЭДС образуют симметричную систему
прямой последовательности, т.е.
.
Генератор симметричен и, следовательно,
его ЭДС образуют симметричную систему
прямой последовательности, т.е.
![]() ,
,
![]() ,
,
![]() так,
что
так,
что
![]() ,
,
![]() ;
;
![]() .
.
![]() Вследствие
замыкания
Вследствие
замыкания
![]() ,
,
![]() ,
,
![]() .
Поэтому положим
.
Поэтому положим
![]() .
.
Система
токов и система напряжений в месте
короткого замыкания несимметрична.
Разложим их на симметричные составляющие
и получим
![]() ,
,
![]() ,
,
![]() и
и
![]() ,
,
![]() ,
,
![]() .
.
Сопротивления цепи для токов нулевой, прямой и обратной последовательности равны , , .


Тогда уравнения Кирхгофа для отдельных последовательностей будут выглядеть следующим образом
![]() ,
,
![]() ,
,
![]() .
(6.3)
.
(6.3)
Из этих уравнений нужно определить токи и напряжения. Сложим уравнения (6.3)
![]() ,
,
учтем,
то
![]() ,
тогда
,
тогда
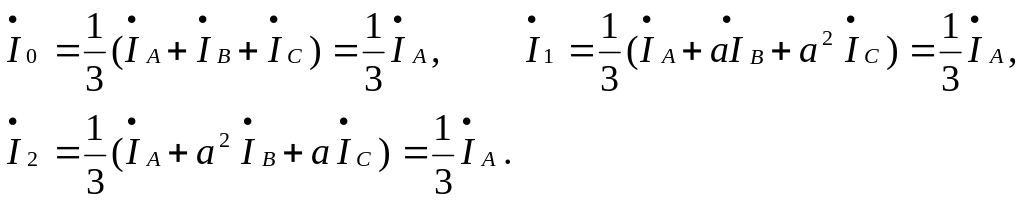
Поэтому втрое уравнение (6.3) переписывается следующим образом
![]() ,
отсюда
,
отсюда
 .
.
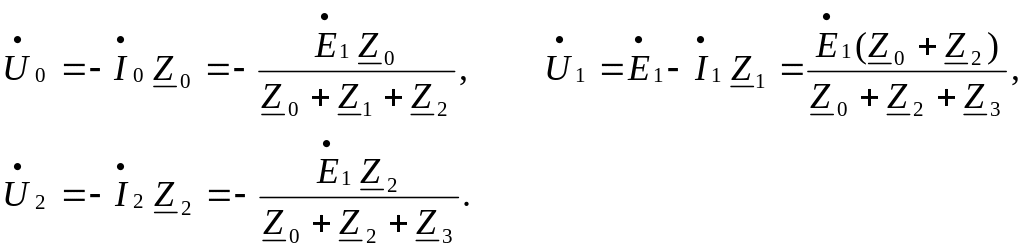
Далее
находим
![]()
